A Funkcija matematikoje yra ypatingas ryšys tarp įvesties reikšmių rinkinio ir išvesties reikšmių rinkinio. Funkcijose kiekviena įvesties reikšmė suteikia tam tikrą išvesties vertę. Matematikos funkciją pavaizduojame kaip, y = f(x) kur x yra įvesties vertė ir kiekvienam x gauname išvesties reikšmę kaip y.

Šiame straipsnyje mes sužinosime apie Matematikos funkcijos, įvairūs jų tipai, pavyzdžiai ir kt.

Turinys

• Kas yra funkcija matematikoje?
• Funkcijų apibrėžimas matematikoje
• Funkcijų pavyzdžiai
• Sąlyga funkcijai atlikti
• Funkcijų vaizdavimas matematikoje
• Funkcijos identifikavimas
• Funkcijų tipai
• Kas yra algebros funkcija?
• Domenas ir funkcijos diapazonas
• Funkcijų sudėtis
• Funkcijų algebra
• Kas yra grafiko funkcija?
• Grafikos funkcijos
• Bendrosios funkcijos
• Funkcijų taikymai
• Funkcijos pavyzdžiai
• Praktikos problemos, kas yra funkcija

Kas yra funkcija matematikoje?

Matematikos funkcija yra a santykį tarp įvesties reikšmių (domeno) ir išvesties reikšmių (diapazono) pateiktų rinkinių taip, kad jokie du kintamieji iš domenų rinkinių nebūtų susieti su tuo pačiu kintamuoju diapazono rinkinyje. Paprastas funkcijos pavyzdys matematikoje yra f(x) = 2x, kuris apibrėžiamas R→R, čia bet kuris srities kintamasis yra susijęs tik su vienu kintamuoju diapazone.

Matematikos funkcija turi domeną, kododomeną ir diapazoną. Domenas yra visų galimų x reikšmių rinkinys, o funkcijos diapazonas yra visų y išvesties reikšmių rinkinys. Diapazonas yra funkcijos kododomeno poaibis. Taip pat galime pasakyti, kad funkcija matematikoje yra ryšys su unikalia išvestimi ir nė viena įvesties reikšmė neturi panašios išvesties funkcijoje, kaip yra santykio atveju.

Funkcijų apibrėžimas matematikoje

Funkcija yra specialus ryšys arba metodas, jungiantis kiekvieną aibės A narį su unikaliu aibės B nariu per apibrėžtą ryšį. Aibė A vadinama domenu, o rinkinys B – funkcijos bendruoju domenu. Funkcija matematikoje nuo aibės A iki aibės B apibrėžiama taip:

f = ∀ a ∈ A, b ∈ B

Kiekviena funkcija yra santykis, bet kiekvienas santykis nėra funkcija. Kriterijai, kad bet koks ryšys būtų laikomas funkcija, nes pagal funkciją kiekvienas aibės A elementas turi tik vieną vaizdą aibėje B, o santykyje aibės A elementas gali turėti daugiau nei vieną vaizdą rinkinyje B.

Matematikoje apibrėžiame funkcijas nuo netuščios aibės A iki netuščios aibės B taip, kad

(a, b) ∈ f, tada f(a) = b

kur skambinom b kaip įvaizdis a apibrėžta pagal ryšį f .

Kiekvienas elementas 'a' rinkinio A turi unikalų vaizdą ' b ' rinkinyje B, tada tai yra funkcija.

Funkcijų pavyzdžiai

Funkcija matematikoje f apibrėžiama taip, y = f(x) kur x yra įvesties reikšmė, o kiekvienai x įvesties reikšmei gauname unikalią y reikšmę. Įvairūs matematikos funkcijų, apibrėžtų R → R, pavyzdžiai:

• y = f(x) = 3x + 4
• y = f(x) = sin x + 3
• y = f(x) = -3x²+3 ir kt

Sąlyga funkcijai atlikti

Bet kurioms dviem netuščioms aibėms A ir B – funkcija f: A → B tai reiškia f yra funkcija nuo A iki B, kur A yra domenas ir B yra bendras domenas.

Bet kuriam elementui a ∈ A, unikalus elementas b ∈ B yra toks, kad (a,b) ∈ f. Unikalus elementas b, susietas su a, žymimas f(a) ir skaitomas kaip f iš a. Tai galima geriau suprasti iš toliau pateikto paveikslėlio:

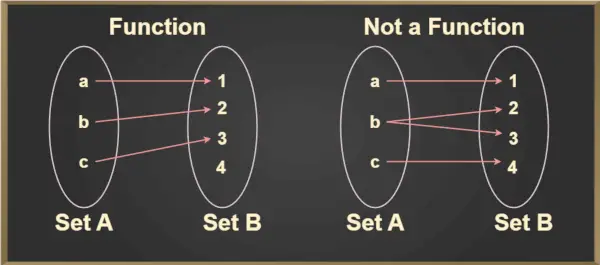
Vertikalios linijos testas

Vertikalios linijos testas naudojamas norint nustatyti, ar kreivė yra funkcija, ar ne. Jei kuri nors kreivė kerta vertikalią liniją daugiau nei viename taške, kreivė nėra funkcija.

Funkcijų vaizdavimas matematikoje

Matematikos funkciją atstovaujame kaip

y = f(x) = x + 3

Čia x reikšmių rinkinys yra funkcijos sritis, o y išvesties reikšmių rinkinys yra funkcijos bendras sritis. Čia funkcija apibrėžiama visiems realiesiems skaičiams, nes suteikia unikalią reikšmę kiekvienam x, tačiau ne visada įmanoma gauti kiekvienos x reikšmės išvestį, tokiu atveju funkciją apibrėžiame iš dviejų dalių, tai galima suprasti kaip

• f(x) = 1/(x – 2), kur x ≠ 2
• f(x) = x²kur x ∈ {R}

Matematikos funkciją galime apibrėžti kaip mašiną, kuri ima tam tikrą įvestį ir suteikia unikalią išvestį. Funkcija f(x) = x²toliau apibrėžiamas kaip

Matematikos funkciją galime pavaizduoti trimis metodais:

• Užsakytų porų rinkinys
• Lentelės forma
• Grafinė forma

Pavyzdžiui, jei funkciją vaizduojame kaip, f(x) = x³

Java sąrašą į masyvą

Kitas būdas pavaizduoti tą pačią funkciją yra kaip užsakytų porų rinkinys kaip,

f = {(1,1), (2,8), (3,27)}

Aukščiau minėtoje aibėje funkcijos sritis yra D = {1, 2, 3}, o funkcijos sritis R = {1, 8, 27}

Funkcijos identifikavimas

Funkcija matematikoje priskiriama specialiam ryšio tipui. Yra šios taisyklės, pagal kurias galima nustatyti funkciją:

• Ryšys, kuriame kiekviena įvestis susieta su unikalia išvestimi, yra funkcija. Tai iškvietė funkciją „vienas su vienu“.
• Ryšys, kuriame dvi įvestis (išankstinis vaizdas) susietos su vienu išėjimu, taip pat yra funkcija. Tai yra daug prieš vieną funkciją.
• Ryšys, kai viena įvestis susieta su dviem skirtingais išėjimais, nėra funkcija.
• Ryšys, kai daug įėjimų susieta su daugybe išėjimų, vadovaujantis jokios konkrečios taisyklės, nėra funkcija.

Funkcijų tipai

Skirtingas Funkcijų tipai yra naudojami įvairių tipų matematinėms problemoms spręsti, ypač susijusioms su kreivėmis ir lygtimis. Matematikoje yra trijų pagrindinių tipų funkcijos, pagrįstos elementų atvaizdavimu nuo aibės A iki aibės B.

Injekcinė funkcija arba funkcija vienas prieš vieną

Funkcija, kurioje kiekvienas domeno elementas turi atskirą vaizdą kodomene, vadinama Injekcinis arba „Vienas su vienu“ funkcija .

f: sakoma, kad A → B yra vienas su vienu arba injekcinis, jei skirtingų A elementų vaizdai pagal f yra skirtingi, t.

f(a ₁ ) = b ₁ , f(a ₂ ) = b ₂

kur₁, a₂∈ A ir b₁, b₂∈ B

Surjektyvinės funkcijos arba Onto funkcija

Surjekcinė funkcija yra funkcija, kurioje kiekvienas kodo domeno elementas turi išankstinį vaizdą domene. Jis taip pat vadinamas Į funkciją o tai reiškia, kad kiekvienas kodomeno elementas yra susietas su kiekvienu domeno elementu. Joks kodomeno elementas neturėtų turėti tuščio ryšio. Kodomeno ir diapazono elementų skaičius yra toks pat.

f: Sakoma, kad A → B yra į, jei kiekvienas B elementas yra kokio nors A elemento atvaizdas pagal f, t. y. kiekvienam b ϵ B, A yra elementas 'a', kad f(a) = b.

Bijekcinė funkcija

Jei funkcija turi ir injekcinės (vienas prieš vieną), ir surjektyviąją (funkcija) savybių, funkcija vadinama Bijekcinė funkcija . Bijektyvinėje funkcijoje kiekvienas domeno elementas yra susijęs su kiekvienu kodomeno elementu, taip pat yra ryšys vienas su vienu. Tai reiškia, kad kodomeno ir diapazono elementų skaičius yra toks pat ir joks elementas nei domene, nei kodomene neturi tuščio ryšio.

Remiantis išvesties reikšmėmis, funkcijos klasifikuojamos kaip nelyginės ir lyginės. Pažvelkime į juos

Nelyginės funkcijos

Nelyginė funkcija yra funkcijos tipas, kuris rodo simetriją kilmei. Tiksliau, jei f(x) yra nelyginė funkcija, ji rodo, kad f(-x) = -f(x)

Net Funkcija

Lyginė funkcija yra funkcijos tipas, pasižymintis simetrija y ašies atžvilgiu. Tiksliau, jei f (x) yra lyginė funkcija, ji rodo, kad f (-x) = f (x)

Kas yra algebros funkcija?

Funkcija viduje algebra yra lygtis, kurios atveju bet kuris x, kurį galima įtraukti į lygtį, iš lygties išves tiksliai vieną išvestį, pvz., y. Jis pavaizduotas kaip y = f(x), kur x yra nepriklausomas kintamasis, o y yra priklausomas kintamasis.

Pavyzdžiui:

• y = 2x + 1
• y = 3x – 2
• y = 4 m
• y = 5/x

Domenas ir funkcijos diapazonas

Domenas ir diapazonas funkcijos yra atitinkamai įvesties ir išvesties reikšmės. Pavyzdžiui, tarkime, kad turime funkciją, pateiktą kaip f (x) = x². Čia mes galime paimti visą realųjį skaičių kaip įvesties x reikšmę, o išvestis visada bus teigiamas tikrasis skaičius. Taigi jo domeną sudaro visi realieji skaičiai, vaizduojami kaip R, o jo diapazonas yra teigiamų realiųjų skaičių, vaizduotų kaip R.⁺

Funkcijų sudėtis

Jei f: A → B ir g: B→ C yra dvi funkcijos. Tada f ir g sudėtis žymima f(g) ir apibrėžiama kaip funkcija rūkas = f(g(x)), kai x ∈ A.

Paimkime dvi funkcijas f(x) = x + 3 ir g(x) = 2x²

rūkas = f(g(x))

⇒ rūkas = f(2x²)

⇒ dantis = 2x²+ 3

Sužinokite daugiau, Funkcijų sudėtis

Funkcijų algebra

Funkcijų algebra apima algebrines operacijas, atliekamas tarp dviejų funkcijų. Algebrinė operacija dviem funkcijoms f(x) ir g(x), apibrėžtoms pagal tikrąją x reikšmę, yra paminėta toliau:

• (f + g) (x) = f (x) + g (x)
• (f – g) (x) = f(x) – g(x)
• (f.g) (x) = f(x).g(x)
• (k f(x)) = k (f(x)); {Jei k yra tikrasis skaičius}
• (f/g)(x) = f(x)/g(x); {G(x) ≠ 0}

Kas yra grafiko funkcija?

Funkciją galima lengvai pavaizduoti diagramoje. Bet kuri grafiko funkcija reiškia kreivę (įskaitant tiesią liniją) x-y plokštumoje, susietoje su jos įvesties ir atitinkamomis išvesties reikšmėmis.

Norėdami nubraižyti funkciją, pirmiausia suraskite keletą taškų, kurie yra ant funkcijos, ir tada sujunkite šiuos taškus pagal funkcijos vietą. Pavyzdžiui, norint pavaizduoti funkciją (tiesią) f(x) = y = 5x – 2, mums reikia tam tikro grafiko taško. Norėdami rasti tašką, grafiko tašką, pirmiausia paimame atsitiktines x reikšmes ir tada randame atitinkamas y reikšmes, kaip

setinterval javascript

f(x) = y = 5x-2

jei x = 0, y = 5(0) – 2 = -2 ⇒ (x, y) = (0, -2)

jei x = 1, y = 5(1) – 2 = 3 ⇒ (x, y) = (1, 3)

jei x = 2, y = 5(2) – 2 = 8 ⇒ (x, y) = (2, 8)

Dabar sujungę šiuos taškus galime gauti funkcijos y = 5x – 2 grafiką

Grafikos funkcijos

Žinant x reikšmes, funkcija f(x) gali būti pavaizduota grafike. Kadangi y = f(x), galime rasti susietą y reikšmę, pradėdami nuo x reikšmių. Dėl to galime nubraižyti grafiką koordinačių plokštumoje naudodami x ir y reikšmes. Apsvarstykite šį scenarijų:

Tarkime, y = x + 3

Kai x = 0, y = 3

Panašiai,

• x = -2, y = -2 + 3 = 1
• x = -1, y = -1 + 3 = 2
• x = 1, y = 1 + 3 = 4
• x = 2, y = 2 + 3 = 5
• x = 3, y = 3 + 3 = 6

Dėl to galime nubraižyti funkcijos x + 3 grafiką naudodami šias reikšmes.

Bendrosios funkcijos

Kai kurios bendrosios funkcijos, dažniausiai naudojamos matematikoje, yra aptariamos toliau:

Tikra funkcija

Tikra funkcija matematikoje reiškia funkciją, kurios domenas ir diapazonas yra realiųjų skaičių poaibiai (žymimi ℝ). Paprasčiau tariant, tikroji funkcija yra matematinė taisyklė arba ryšys, priskiriantis realiojo skaičiaus reikšmę kiekvienai realaus skaičiaus įvestis.

Realios funkcijos

Polinominė funkcija

Funkcija, kurioje algebrinių kintamųjų eksponentai yra neneigiami sveikieji skaičiai, vadinama Polinominė funkcija . Jei kintamojo laipsnis yra 1, tai vadinama tiesine funkcija, jei laipsnis yra 2, tai kvadratine funkcija, o jei laipsnis yra 3, tai vadinama kubine funkcija. Toliau pateikiami keli daugianario funkcijų pavyzdžiai:

• y = x²
• y = 2x + 3
• y = 3x³

Polinominę funkciją galima toliau suskirstyti į šiuos tipus:

Linijinė funkcija : Tiesinė funkcija yra tos, kuriose didžiausia kintamojo galia yra 1. Bendroji forma Linijinė funkcija yra y = mx + c

Kvadratinė funkcija : Kvadratinė funkcija yra tos, kuriose didžiausia kintamojo galia yra 2. Bendroji forma kvadratinė funkcija yra, kirvis ² + bx + c = 0

Kubinė funkcija : Kubinė funkcija yra tie, kuriuose didžiausia kintamojo galia yra 3. Bendroji Kubinės funkcijos forma pateikiama kaip kirvis ³ + bx ² + cx + d = 0

Atvirkštinė funkcija

Atvirkštinė funkcija yra funkcija, turinti kitos funkcijos atvirkštinę vertę. Tarkime, kad turime funkciją y = f(x), tada jos atvirkštinė funkcija bus x = f^-1(y). Jei y = f (x), sritis yra x, o diapazonas yra y, o tuo atveju, kai x = f^-1(y), domenas yra y, o diapazonas yra x. Taigi galime pasakyti, kad pradinės funkcijos sritis yra jos atvirkštinės funkcijos sritis, o pradinės funkcijos sritis yra pradinės funkcijos sritis. Kai kurie atvirkštinių funkcijų pavyzdžiai:

• y = taip^-1(x)
• y = x^-1

Sritys funkcija

Ploto funkcija paprastai reiškia matematinę funkciją, kuri apskaičiuoja geometrinės figūros ar srities plotą. Sritys funkcija paima vieną ar daugiau parametrų kaip įvestį ir grąžina atitinkamos formos plotą. Kai kurios zonos funkcijos aptariamos toliau:

Apskritimo funkcijos sritis : Apskritimo sritis (A) yra jo spindulio (r) funkcija, kad

A = πr ²

Trikampio funkcijos sritis : Trikampio plotas (A) yra jo pagrindo (b) ir aukščio (h) funkcija, todėl

A = (bh)/2

Eksponentinė funkcija

Eksponentinė funkcija yra ta, kuri pavaizduota kaip f(x) = e^x. Jis dažnai naudojamas norint parodyti greitą augimą ar nykimą.

Logaritminė funkcija

Logaritminė funkcija yra matematinė funkcija, vaizduojanti atvirkštinį eksponencijos veiksmą. Jis pavaizduotas kaip f(x) = log x.

Lubų funkcija

Lubų funkcija , žymimas ⌈x⌉, apvalina realųjį skaičių x iki artimiausio sveikojo skaičiaus, kuris yra didesnis arba lygus x. Kitaip tariant, ji randa mažiausią sveikojo skaičiaus reikšmę, kuri yra didesnė arba lygi x.

Grindų funkcija

Grindų funkcija, žymima ⌊x⌋, realųjį skaičių x apvalina iki artimiausio sveikojo skaičiaus, kuris yra mažesnis arba lygus x. Kitaip tariant, ji suranda didžiausią sveikojo skaičiaus reikšmę, kuri yra mažesnė arba lygi x.

Modulio funkcija

Modulio funkcija , taip pat žinomas kaip absoliučios reikšmės funkcija, grąžina tikrojo skaičiaus dydį arba dydį, neatsižvelgiant į jo ženklą. Modulio funkcija žymima kaip ∣x∣, kur x yra įvesties reikšmė.

linux komandos, kurios

Signum funkcija

Signum funkcija , taip pat žinomas kaip ženklo funkcija arba ženklo funkcija, yra matematinė funkcija, kuri grąžina tikrojo skaičiaus ženklą. Tai rodo, ar skaičius yra teigiamas, neigiamas ar nulis.

Trigonometrinės funkcijos

Trigonometrinės funkcijos yra matematinės funkcijos, susiejančios stačiojo trikampio kampus su jo kraštinių ilgiais. Šešios pagrindinės trigonometrinės funkcijos yra sinusas (sin), kosinusas (cos), tangentas (tangentas), kosekantas (cosec), sekantas (sec) ir kotangentas (cot).

Sudėtingos funkcijos

Bet kuri funkcija, kurios įvesties kintamieji yra sudėtinga funkcija, vadinama kompleksine funkcija. Kompleksinis skaičius yra skaičius, kurį galima nubraižyti kompleksinėje plokštumoje. A kompleksinis skaičius turime realųjį ir įsivaizduojamą skaičių. Kompleksinis skaičius (z) pavaizduotas kaip, z= x + iy, o kompleksinė funkcija pavaizduota kaip, f(z) = P(x, y) + iQ(x, y)

Funkcijų taikymai

Kai sakome, kad kintamasis dydis y yra kintamojo dydžio x funkcija, nurodome, kad y priklauso nuo x, o y reikšmę lemia x reikšmė. Šią priklausomybę galima išreikšti taip: f = y (x).

• Apskritimo spindulys gali būti naudojamas apskritimo plotui apskaičiuoti. Spindulys r veikia plotą A. Paskelbiame, kad A yra r funkcija matematinėje funkcijų kalboje. Galime parašyti A = f(r) =π×r²
• Sferos tūris V yra jos spindulio funkcija. V = f(r) = 4/3 × r³žymi V priklausomybę nuo r.
• Jėga yra kūno, kurio masė yra m, pagreičio funkcija. F = g(a) = m×a.

Žmonės taip pat skaito:

• Ryšys ir funkcija
  
• Trigonometrinių funkcijų sritis ir diapazonas
• Funkcijos diapazonas
• Hiperbolinė funkcija

Funkcijos pavyzdžiai

1 pavyzdys: Dvi funkcijos f ir g apibrėžiamos taip, kad f(x) = x ² ir g(x) = ln(2x). Raskite sudėtinę funkciją (gof )( x )

Sprendimas:

Duota:

• f(x) = x²
• g(x) = ln(2x)

(gof )( x ) = g (f (x))

[g (f (x)] = ln (2f (x))

= ln(2x²)

= 2 ln (√2x)

Taigi (gof)(x) = 2 ln(√2x)

2 pavyzdys: Raskite funkcijos g(t)= 6t išvestį ² + 5 val

• (i) t = 0
• (ii) t = 2

Sprendimas:

Suteikta funkcija,

g(t)= 6t²+ 5t

• (i) t = 0

g(0) = 6(0)²+5(0) = 0 + 0

g(0) = 0

• (ii) t = 2

g(2) = 6(2)²+5(2)

g(2) = 24 + 10

g(2) = 34

3 pavyzdys: stačiakampio ilgis yra penkis kartus didesnis už jo plotį, išreikškite stačiakampio plotą kaip jo ilgio funkciją.

Sprendimas:

Tegu stačiakampio ilgis yra l, o stačiakampio plotis yra b

Dabar

• b = l/5

Stačiakampio (A) plotas = l × l/5 = l²/5

string jsonobject

Taigi stačiakampio plotas kaip jo ilgio funkcija yra

A(l) = l ² /5

Praktikos problemos, kas yra funkcija

1. Duota funkcija f(x)=3x+5

• Rasti f(2)
• Rasti f(−1)
• Nustatykite funkcijos sritį ir diapazoną.

2. Duota funkcija g(x)=x ² – 4x + 3

• Raskite funkcijos šaknis.
• Raskite g(3) ir g(0).
• Nustatykite funkcijos viršūnę.

3. Duotos dvi funkcijos f(x)=x + 2 ir h(x)=2x – 3

• Raskite sudėtinę funkciją (f ∘ h) (x)
• Įvertinti (f ∘ h)(2)

Santrauka – kas yra funkcija

Matematikos funkcija yra ypatingas ryšys tarp įvesties verčių (domeno) ir išvesties reikšmių (diapazonas), kai kiekviena įvestis yra susieta su unikalia išvestimi. Funkcijos, pavaizduotos kaip y = f(x), turi specifines charakteristikas ir gali būti vizualizuojamos naudojant sutvarkytas poras, lenteles arba grafikus. Jie yra būtini sprendžiant įvairias matematines problemas ir būna įvairių tipų, įskaitant injekcinius (vienas su vienu), surjektyvius (įskaitant) ir bijektyvius (abu). Funkcijos gali būti tikrinamos naudojant vertikalios linijos testą ir toliau skirstomos į polinomines, atvirkštines, eksponencines, logaritmines ir trigonometrines funkcijas. Norint suprasti funkcijas, reikia atpažinti jų sritį, diapazoną ir jas apibrėžiančias taisykles. Pavyzdžiai apima paprastas linijines funkcijas, pvz y = 2x + 1 ir sudėtingos funkcijų kompozicijos. Funkcijos vaidina lemiamą vaidmenį algebroje, geometrijoje ir skaičiavimuose, padedančios vaizduoti ir analizuoti matematinius ryšius ir realaus pasaulio reiškinius.

DUK apie tai, kas yra funkcija

Koks yra funkcijos apibrėžimas?

Ryšys f, apibrėžtas aibėje A su kita aibe B, matematikoje vadinamas funkcija, jei kiekviena A reikšmė rinkinyje B turi unikalią reikšmę.

Kaip parašyti funkciją matematikoje?

Funkcija f matematikoje vaizduojama kaip f: A → B ir apibrėžiama kaip, f(x) = x + 2. Čia kiekvienai unikaliai x vertei turime unikalią y reikšmę.

Kaip pakeisti funkciją?

Mes galime lengvai transformuoti funkciją į kitas funkcijas, tiesiog atlikdami pagrindines funkcijos algebrines operacijas. Skirtingos funkcijos transformacijos yra atspindys, vertimas, sukimas ir kt.

Kas yra racionali funkcija?

Trupmenų funkcija, kai skaitiklis ir vardiklis yra daugianario funkcijos, vadinama racionalia funkcija. Kai kurie racionalios funkcijos pavyzdžiai:

• f(x) = x ² /(2x + 3)
• g(x) = (6x + 3)/(x – 1), ir tt

Kas yra tiesinė funkcija?

Algebrinė funkcija, kurioje kiekvienas funkcijos narys yra pastovus arba turi vieną laipsnį, vadinama tiesine funkcija. Kai kurie linijinės funkcijos pavyzdžiai:

• f(x) = 2x + 3
• g(x) = x – 5 ir kt.

Kas yra funkcijos domenas ir kodomenas?

Jei apibrėžiame funkciją kaip, y = f(x). Tada x sritis yra visos x reikšmės, kurių y lemia unikalią reikšmę. O bendras y domenas yra visų y reikšmių rinkinys kiekvienai x reikšmei.

Kaip atpažįstate funkciją matematikoje?

Jei bet kuri santykio domeno įvesties reikšmė (x) turi daugiau nei vieną vaizdą (y), tada šie santykiai niekada negali būti funkcija. Taigi, jei x reikšmė kartojasi sutvarkytoje poroje, tai niekada nėra funkcija.