Sudėtiniai skaičiai yra natūralus realiųjų skaičių tęsinys. Šiuolaikiniais laikais kompleksiniai skaičiai naudojami daugelyje sričių, tokių kaip skaitmeninis signalų apdorojimas, kriptografija ir daugelyje su kompiuteriais susijusių sričių.

Šiame straipsnyje sužinosime apie įsivaizduojamus skaičius, kompleksinius skaičius ir jų tipą, įvairias operacijas su kompleksiniais skaičiais, kompleksinių skaičių savybes, kompleksinių skaičių taikymą ir kt.

Sudėtingų skaičių apibrėžimas

Sudėtingi skaičiai yra numeriai formos (a + i b) kur a & b yra tikrieji skaičiai ir i yra įsivaizduojamas vienetas, vadinamas iota, kuris reiškia √-1. Pavyzdžiui, 2 + 3i yra kompleksinis skaičius, kuriame 2 yra tikrasis skaičius, o 3i yra įsivaizduojamas skaičius. Sudėtiniai skaičiai gali būti parašyti kaip a + ib, kur a ir b yra racionalūs skaičiai, kurie gali būti pavaizduoti skaičių eilutėje, besitęsiančioje iki begalybė .

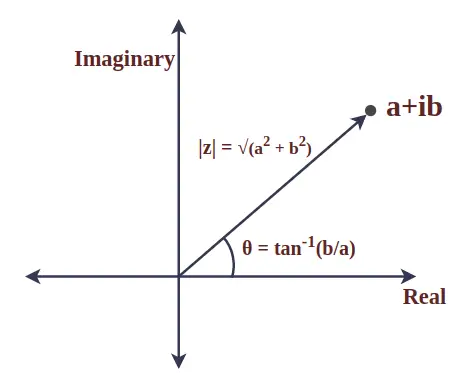
Kompleksinio skaičiaus modulis

Sudėtinio skaičiaus modulis yra absoliuti reikšmė ir reiškia atstumą tarp pradžios ir nurodyto taško. Jis taip pat žinomas kaip kompleksinio skaičiaus dydis. Panagrinėkime kompleksinį skaičių z = a + ib, tada z modulis apibrėžiamas taip:

|z| = √(a ² + b ² )

kur,

• a yra tikroji kompleksinio skaičiaus z dalis ir
• b yra įsivaizduojama kompleksinio skaičiaus z dalis.

Kompleksinio skaičiaus argumentas

Kampas tarp kompleksinio skaičiaus spindulio vektoriaus ir teigiamos x ašies vadinamas kompleksinio skaičiaus argumentu. Kompleksiniam skaičiui z = a + ib jis matematiškai apskaičiuojamas taip:

θ = įdegis ^-1 (b/a)

kur,

• a yra tikroji kompleksinio skaičiaus z dalis ir
• b yra įsivaizduojama kompleksinio skaičiaus z dalis.

i (iota) galia

I(iota) apibrėžiamas kaip -1 kvadratinė šaknis. Taigi bet kuri i galia gali būti išreikšta kaip pakartotinis i dauginimas iš savęs, t.y.

• i = √(-1)
• i²= -1
• i³= – i
• i⁴= 1
• i⁵= i
• i⁶= – 1
• ir taip toliau..

Sudėtingų skaičių poreikis

Senovėje žmonės žinojo tik apie natūraliuosius skaičius numeriai yra intuityviausi, nes žmogaus smegenys jas jau supranta, naudodamos tokius dalykus kaip avys ir maistas. Taigi mes turime tik natūraliųjų skaičių aibę ( N ), tačiau natūraliuose skaičiuose lygties x + a = b (a> b) ir a, b ∈ N sprendinių nėra. Taigi atsirado natūraliųjų skaičių plėtinys, ty sveikieji skaičiai ( aš ).

Dabar šioje skaičių aibėje nėra lygties sprendinio, ax = b (a ≠ 0) ir a, b ∈ I, kur a ir b yra sveikieji skaičiai. Taigi sveikųjų skaičių aibė (I) išplečiama iki racionaliųjų skaičių ( K ).

Vėlgi, šioje racionaliųjų skaičių rinkinyje nėra lygties x sprendimo²= a (a> 0) ir a ∈ Q. Taigi, K yra išplėstas, kad apimtų tokius skaičius, kad x²= a(jei a> 0) t.y., neracionalieji skaičiai. Šis rinkinys pavadintas Realiais skaičiais ir jį atstovauja R .

Dabar ilgą laiką buvo manoma, kad mums nereikia išplėsti šio realiųjų skaičių rinkinio, kad sudarytume kitą didesnį rinkinį, nes ši skaičių rinkinys atrodo baigtas. Tačiau šioje skaičių rinkinyje vėl iškilo nauja problema, t. y. nėra tikrojo skaičiaus, kurio x²= a (a <0) ir a ∈ R. Taigi realiųjų skaičių aibė dar išplečiama, kad apimtų visas tokias vertes ir pavadintas kompleksiniais skaičiais. C .

Kompleksinių skaičių klasifikacija

Kaip žinome, standartinė kompleksinio skaičiaus forma yra z = (a + i b) kur a, b ∈ R ir i yra iota (įsivaizduojamas vienetas). Taigi, atsižvelgiant į a (vadinamą tikrąja dalimi) ir b (vadinamąja dalimi) reikšmes, kompleksiniai skaičiai skirstomi į keturis tipus:

• Nulis kompleksinis skaičius
• Grynai tikri skaičiai
• Grynai įsivaizduojami skaičiai
• Įsivaizduojami skaičiai

Sužinokime apie šias rūšis išsamiai.

Nulis kompleksinis skaičius

Bet kuriam kompleksiniam skaičiui z = a + ib, jei a = 0 ir b = 0, kompleksinis skaičius vadinamas nuliniu kompleksiniu skaičiumi. Pavyzdžiui, vienintelis pavyzdys yra 0.

Grynai tikri skaičiai

Bet kuriam kompleksiniam skaičiui z = a + ib, jei a ≠ 0 & b = 0, kompleksinis skaičius vadinamas grynai realiuoju skaičiumi, ty skaičiumi be įsivaizduojamos dalies. Visi tikrieji skaičiai yra to pavyzdžiai, pavyzdžiui, 2, 3, 5, 7 ir tt.

Grynai įsivaizduojami skaičiai

Bet kuriam kompleksiniam skaičiui z = a + ib, jei a = 0 & b ≠ 0, kompleksinis skaičius vadinamas grynai įsivaizduojamu skaičiumi, ty skaičiumi be tikrosios dalies. Visi skaičiai be realių dalių yra šio tipo skaičių pavyzdžiai, ty -7i, -5i, -i, i, 5i, 7i ir kt.

Įsivaizduojami skaičiai

Bet kuriam kompleksiniam skaičiui z = a + ib, jei a ≠ 0 ir b ≠ 0, kompleksinis skaičius vadinamas įsivaizduojamas skaičius . Pavyzdžiui, (-1 – i), (1 + i), (1 – i), (2 + 3i) ir kt.

Įvairios sudėtingų skaičių formos

Yra įvairių formų kompleksinių skaičių, kurie yra,

• Stačiakampio formos
• Poliarinė forma
• Eksponentinė forma

Dabar sužinokime apie juos išsamiai.

Stačiakampio formos

Stačiakampio formos yra taip pat vadinama Standartinė forma ir jį atstovauja (a + ib), kur a ir b yra tikrieji skaičiai.

Pavyzdžiui: (5 + 5i), (-7i), (-3 – 4i) ir kt.

Poliarinė forma

Poliarinė forma yra kompleksinio skaičiaus, kuriame polinės koordinatės vaizduojamos [kur koordinatės vaizduojamos kaip (r, θ), kur r yra atstumas nuo pradžios, o θ yra kampas tarp linijos, jungiančios tašką ir pradžią, ir teigiamos x ašies) naudojami kompleksiniam skaičiui pavaizduoti. Bet koks kompleksinis skaičius vaizduojamas kaip r [cos θ + i sin θ].

Pavyzdžiui: [cos π/2 + i sin π/2], 5[cos π/6 + i sin π/6] ir kt.

Eksponentinė forma

Eksponentinės kompleksinių skaičių formos yra kompleksinių skaičių vaizdavimas naudojant Eulerio formulę, o šioje formoje kompleksinis skaičius vaizduojamas reⁱ, kur r yra taško atstumas nuo pradžios, o θ yra kampas tarp teigiamos x ašies ir spindulio vektoriaus.

Pavyzdžiui: e^{aš (0)}, Tai yra^i(π/2), 5.e^i(π/6)ir kt.

Pastaba: Visos trys aukščiau aptartų kompleksinių skaičių formos yra tarpusavyje konvertuojamos, t. y. jas galima labai lengvai konvertuoti iš vienos formos į kitą.

Operacijos su sudėtingais skaičiais

Su kompleksiniais skaičiais galima atlikti šias operacijas:

• Papildymas
• Atimtis
• Daugyba
• Padalinys
• Konjugacija

Sudėtinių skaičių pridėjimas

Galime pridėti du kompleksinius skaičius, tiesiog sudėdami jų tikrąją ir įsivaizduojamą dalis atskirai.

Pavyzdžiui, (3 + 2i) + (1 + 4i) = 4 + 6i.

Kompleksinių skaičių atėmimas

Galime atimti du kompleksinius skaičius, tiesiog atskirdami jų tikrąją ir įsivaizduojamą dalis.

Pavyzdžiui, (3 + 2i) – (1 + 4i) = 2 – 2i.

Kompleksinių skaičių daugyba

Mes galime padauginti du kompleksinius skaičius, naudodami paskirstymo savybę ir tai, kad i²= -1.

Pavyzdžiui, (3 + 2i) (1 + 4i) = 3 + 12i + 2i + 8i²= 3 + 14i – 8 = -5 + 14i.

Kompleksinių skaičių padalijimas

Vieną kompleksinį skaičių galime padalyti iš kito, tiesiog padaugindami tiek skaitiklį, tiek vardiklį iš kompleksinio vardiklio konjugato ir dar labiau supaprastindami išraišką.

Pavyzdžiui, (3 + 2i)/(1 + 4i) = (3 + 2i)(1 – 4i)/(1 + 4i)(1 – 4i) = (11 – 10i)/17.

Kompleksinių skaičių konjugacija

Mes galime lengvai rasti kompleksinio skaičiaus konjugatas, tiesiog pakeičiant jo įsivaizduojamos dalies ženklą. Kompleksinio skaičiaus konjugatas dažnai žymimas juostele virš skaičiaus, pvz., z̄.

Pavyzdžiui, 3 + 2i konjugatas yra 3 – 2i.

Sudėtingų skaičių tapatybės

Bet kokiems dviem kompleksiniams skaičiams z₁ir z₂galima pateikti šias algebrines tapatybes:

• (Su ₁ + z ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² + 2 z ₁ × z ₂
• (Su ₁ - Su ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² – 2 z ₁ × z ₂
• (Su ₁ ) ² - (Su ₂ ) ² = (z ₁ + z ₂ )(Su ₁ - Su ₂ )
• (Su ₁ + z ₂ ) ³ = (z ₁ ) ³ + 3 (z ₁ ) ² Su ₂ +3(z ₂ ) ² Su ₁ + (z ₂ ) ³
• (Su ₁ - Su ₂ ) ³ = (z ₁ ) ³ – 3 (z ₁ ) ² Su ₂ +3(z ₂ ) ² Su ₁ - (Su ₂ ) ³

Su kompleksiniais skaičiais susijusios formulės

Yra keletas formulių, susijusių su kompleksiniais skaičiais, kai kurios iš jų yra tokios:

Eulerio formulė

Eulerio formulė rodo santykį tarp įsivaizduojamos eksponento galios ir trigonometrinio santykio sin ir cos ir yra pateikiama taip:

tai yra ^ix = cos x + i sin x

De Moivre'o formulė

De Moivre'o formulė išreiškia n^thkompleksinio skaičiaus galia poliarine forma ir gaunama taip:

(cos x + i sin x) ⁿ = cos(nx) + i sin(nx)

Sudėtinga plokštuma

Plokštuma, kurioje kompleksiniai skaičiai pavaizduoti vienareikšmiškai, vadinama kompleksine plokštuma arba Argando plokštuma arba Gauso plokštuma.

Kompleksinė plokštuma turi dvi ašis:

• X ašis arba tikroji ašis
• Y ašis arba įsivaizduojama ašis

X ašis arba tikroji ašis

• Visi grynai realūs kompleksiniai skaičiai yra vienareikšmiškai pavaizduoti tašku.
• Visų kompleksinių skaičių realioji dalis Re(z) brėžiama jos atžvilgiu.
• Štai kodėl X ašis taip pat vadinama Tikra ašis .

Y ašis arba įsivaizduojama ašis

• Visi tik įsivaizduojami kompleksiniai skaičiai yra vienareikšmiškai pavaizduoti tašku.
• Įsivaizduojama visų kompleksinių skaičių dalis Im(z) brėžiama jos atžvilgiu.
• Štai kodėl Y ašis taip pat vadinama Įsivaizduojama ašis .

Geometrinis kompleksinių skaičių vaizdavimas

Kaip žinome, kiekvienas kompleksinis skaičius (z = a + i b) yra pavaizduotas unikaliu tašku p(a, b) kompleksinėje plokštumoje, o kiekvienas kompleksinės plokštumos taškas yra unikalus kompleksinis skaičius.

Norėdami pavaizduoti bet kurį kompleksinį skaičių z = (a + i b) kompleksinėje plokštumoje, vadovaukitės šiais susitarimais:

• Realioji z dalis (Re(z) = a) tampa taško p X koordinate

• Įsivaizduojama z dalis (Im(z) = b) tampa taško p Y koordinate

Ir galiausiai z (a + i b) ⇒ p (a, b), kuris yra kompleksinės plokštumos taškas.

Kompleksinių skaičių savybės

Yra įvairių kompleksinių skaičių savybių, kai kurios iš jų yra tokios:

• Bet kuriam kompleksiniam skaičiui z = a + ib, jei z = 0, tada a = 0, taip pat b = 0.
• 4 realiesiems skaičiams a, b, c ir d, kad z₁= a + ib ir z₂= c + id. Jei z₁= z₂tada a = c ir b = d.
• Sudėjus kompleksinį skaičių su jo konjugatu, gaunamas grynai realusis skaičius, ty z + z̄ = tikrasis skaičius.

Tegul z = a + ib,

z + z̄ = a + vienas + a – vienas

⇒ z + z̄ = 2a (tai yra tikra)

• Kompleksinio skaičiaus sandauga su konjuguotais rezultatais taip pat yra grynai tikrasis skaičius, t. y. z × z̄ = tikrasis skaičius

Tada tegul z = a + ib

z × z̄ = (a + vienas) × (a – vienas)

⇒ z × z̄= a²– i²b²

⇒ z × z̄ = a²+ b²(kas yra grynai tikra)

• Sudėtiniai skaičiai yra komutacinės pagal sudėties ir daugybos operaciją. Panagrinėkime du kompleksinius skaičius z₁ir z₂, ir tada

Su ₁ +z ₂ = z ₂ +z ₁

Su ₁ × z ₂ = z ₂ × z ₁

• Sudėtiniai skaičiai yra asociatyvus su sudėties ir daugybos operacija. Panagrinėkime tris kompleksinius skaičius z₁, Su₂, ir z₃tada

(Su ₁ +z ₂ ) +z ₃ = z ₁ + (z ₂ +z ₃ )

(Su ₁ ×z ₂ )×z ₃ = z ₁ ×(z ₂ ×z ₃ )

• Sudėtiniai skaičiai turi paskirstymo nuosavybė taip pat daugybos iš sudėjimo. Panagrinėkime tris kompleksinius skaičius z₁, Su₂, ir z₃tada

Su ₁ ×(z ₂ +z ₃ ) = z ₁ ×z ₂ + z ₁ ×z ₃

Skaityti daugiau,

• Sudėtinių skaičių dalyba
• Z juosta kompleksiniais skaičiais

Kompleksinių skaičių pavyzdžiai

1 pavyzdys: Nubraižykite šiuos kompleksinius skaičius z = 3 + 2i kompleksinėje plokštumoje.

Sprendimas:

Duota:

Su = 3 + 2 i

Taigi, taškas yra z(3, 2). Dabar mes nubraižome šį tašką žemiau esančiame grafike, čia x ašis reiškia tikrąją dalį, o y ašis reiškia įsivaizduojamą dalį.

elektroninės bankininkystės apribojimai

2 pavyzdys: Nubraižykite šiuos kompleksinius skaičius z ₁ = (2 + 2 i), z ₂ = (-2 + 3 i), z ₃ = (-1 – 3 i), z ₄ = (1 – i) kompleksinėje plokštumoje.

Sprendimas:

Duota:

Su₁= (2 + 2 i)

Su₂= (-2 + 3 i)

Su₃= (-1 – 3 i)

Su₄= (1 – i)

Taigi taškai yra z₁(2, 2), z₂(-2, 3), z₃(-1, -3) ir z₄(1, -1). Dabar mes pavaizduojame šiuos taškus žemiau esančiame grafike, čia x ašis reiškia tikrąją dalį, o y ašis reiškia įsivaizduojamą dalį.

DUK apie sudėtingus skaičius

Apibrėžkite kompleksinius skaičius.

Skaičiai, kurių forma yra a+ib, vadinami kompleksiniais skaičiais, kur a ir b yra tikrasis skaičius, o i yra įsivaizduojamas vienetas, reiškiantis kvadratinę šaknį iš -1.

Kuo skiriasi realusis skaičius ir kompleksinis skaičius?

Skirtumas tarp realiųjų ir kompleksinių skaičių yra tas, kad mums reikia tik vieno skaičiaus, kad būtų pavaizduotas bet koks tikrasis skaičius, bet reikia dviejų realiųjų skaičių, kad būtų pavaizduotas bet koks kompleksinis skaičius.

Kokia yra tikroji ir įsivaizduojama kompleksinio skaičiaus dalis?

Kompleksiniame skaičiuje a + ib a yra tikroji kompleksinio skaičiaus dalis, o b vadinama įsivaizduojama kompleksinio skaičiaus dalimi.

Kas yra sudėtingas kompleksinio skaičiaus konjugatas?

Kompleksiniam skaičiui a + ib a – ib vadinamas jo kompleksiniu konjugatu. Sudėtingus konjugatus galima rasti tiesiog pakeitus įsivaizduojamos dalies ženklą.

Koks yra kompleksinio skaičiaus modulis?

Atstumas nuo pradžios iki taško, pavaizduoto kompleksiniu skaičiumi argando plokštumoje, vadinamas viso skaičiaus moduliu, o jei z = a + ib, jis matematiškai apskaičiuojamas taip:

|z| = √(a ² + b ² )

Koks yra kompleksinio skaičiaus argumentas?

Kampas tarp kompleksinio skaičiaus spindulio vektoriaus ir teigiamos x ašies vadinamas kompleksinio skaičiaus argumentu, o jei z = a + ib, jis matematiškai pateikiamas taip:

θ = įdegis ^-1 (b/a)

Kokia yra kompleksinio skaičiaus polinė forma?

Bet kurio kompleksinio skaičiaus, z = a + ib, poliarinė forma pateikiama taip:

r [cos θ + i sin θ]

Kas yra Eulerio formulė?

Eulerio formulė parodo santykį tarp įsivaizduojamos eksponento galios ir trigonometrinio santykio sin ir cos ir yra pateikiama taip:

tai yra ^ix = cos x + i sin x