logo

TechCodeview

Įterpimas į AVL medį

AVL medis:

AVL medis yra savaime balansuojantis dvejetainis paieškos medis ( BST ), kur kairiojo ir dešiniojo pomedžio aukščių skirtumas negali būti didesnis kaip vienas visiems mazgams.

AVL medžio pavyzdys:



Aukščiau pateiktas medis yra AVL, nes kiekvieno mazgo kairiojo ir dešiniojo pomedžio aukščių skirtumai yra mažesni arba lygūs 1.

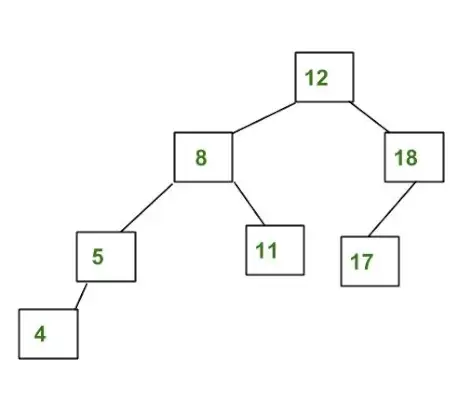
Medžio, kuris nėra AVL medis, pavyzdys:

Aukščiau pateiktas medis nėra AVL, nes 8 ir 12 kairiojo ir dešiniojo pomedžio aukščių skirtumai yra didesni nei 1.



Kodėl AVL medžiai?

Dauguma BST operacijų (pvz., paieška, maksimalus, min., įterpimas, ištrynimas.. ir tt) atliekamos Oi) laikas kur h yra BST aukštis. Šių operacijų kaina gali tapti O(n) dėl iškreiptas Dvejetainis medis . Jeigu pasirūpinsime, kad medžio aukštis išliktų O(log(n)) po kiekvieno įterpimo ir ištrynimo galime garantuoti viršutinę ribą O(log(n)) visoms šioms operacijoms. AVL medžio aukštis visada yra O(log(n)) kur n yra medžio mazgų skaičius.

Įdėjimas AVL medyje:

Norėdami įsitikinti, kad nurodytas medis išliks AVL po kiekvieno įterpimo, turime papildyti standartinę BST įterpimo operaciją, kad atliktume tam tikrą balansavimą.
Toliau pateikiamos dvi pagrindinės operacijos, kurias galima atlikti norint subalansuoti BST nepažeidžiant BST savybės (raktai (kairėje)

  • Rotacija į kairę
  • Teisingas sukimasis
T1, T2 and T3 are subtrees of the tree, rooted with y (on the left side) or x (on the right side) y x /  Right Rotation /  x T3 - - - - - - ->T1 ir / <- - - - - - - /  T1 T2 Left Rotation T2 T3 Keys in both of the above trees follow the following order keys(T1) < key(x) < keys(T2) < key(y) < keys(T3) So BST property is not violated anywhere.>
Rekomenduojama praktika AVL medžio įterpimas Išbandykite!

Veiksmai, kuriuos reikia atlikti įterpiant:

Tegul naujai įdėtas mazgas būna Į



  • Atlikite standartą BST įterpti už Į .
  • Pradėti nuo Į , keliaukite aukštyn ir suraskite pirmąjį nesubalansuotas mazgas . Leisti Su būti pirmuoju nesubalansuotu mazgu, ir Būti vaikas apie Su kuris ateina kelyje iš Į į Su ir x Būti anūkas apie Su kuris ateina kelyje iš Į į Su .
  • Iš naujo subalansuokite medį, atlikdami atitinkamus pasukimus ant pomedžio, įsišaknijusio su Su. Gali būti 4 galimi atvejai, kuriuos reikia tvarkyti kaip x,y ir Su galima išdėstyti 4 būdais.
  • Toliau pateikiami 4 galimi susitarimai:
    • y yra kairysis z vaikas, o x yra kairysis y vaikas (kairioji raidė)
    • y yra kairysis z antrasis, o x yra dešinysis y antrasis (kairysis dešinysis didžioji raidė)
    • y yra tinkamas z vaikas, o x yra tinkamas y vaikas (dešinysis dešinysis atvejis)
    • y yra dešinysis z vaikas, o x yra kairysis y vaikas (dešinė kairioji raidė)

Toliau pateikiamos operacijos, kurios turi būti atliekamos aukščiau minėtais 4 atvejais. Visais atvejais mums tereikia iš naujo subalansuoti submedis įsišaknijęs su Su ir visas medis tampa subalansuotas, kai pomedžio aukštis (Po atitinkamų pasukimų) įsišaknijęs Su tampa toks pat, koks buvo prieš įvedimą.

1. Kairysis kairysis dėklas 

T1, T2, T3 and T4 are subtrees. z y /  /  y T4 Right Rotate (z) x z /  - - - - - - - - ->/  /  x T3 T1 T2 T3 T4 /  T1 T2>

2. Kairysis dešinysis dėklas 

 z z x /  /  /  y T4 Left Rotate (y) x T4 Right Rotate(z) y z /  - - - - - - - - ->/  - - - - - - - -> /  /  T1 x y T3 T1 T2 T3 T4 /  /  T2 T3 T1 T2>

3. Teisingas dešinysis atvejis 

 z y /  /  T1 y Left Rotate(z) z x /  - - - - - - - ->/  /  T2 x T1 T2 T3 T4 /  T3 T4>

4. Dešinysis kairysis dėklas 

 z z x /  /  /  T1 y Right Rotate (y) T1 x Left Rotate(z) z y /  - - - - - - - - ->/  - - - - - - - -> /  /  x T4 T2 y T1 T2 T3 T4 /  /  T2 T3 T3 T4>

Įterpimo prie AVL medžio iliustracija

nuimtas objektyvas1

avlinsert2-jpg

avlinsert3

avlinsert4

avlinsert5

Metodas:

Idėja yra naudoti rekursinį BST įterpimą, po įterpimo gauname nuorodas į visus protėvius po vieną iš apačios į viršų. Taigi, norint keliauti aukštyn, mums nereikia tėvų rodyklės. Pats rekursyvus kodas keliauja aukštyn ir aplanko visus naujai įterpto mazgo protėvius.

Norėdami įgyvendinti idėją, atlikite toliau nurodytus veiksmus:

  • Atlikite įprastą BST įterpimas.
  • Dabartinis mazgas turi būti vienas iš naujai įterpto mazgo protėvių. Atnaujinkite aukščio dabartinio mazgo.
  • Gaukite balanso koeficientą (kairiojo pomedžio aukštis – dešiniojo pomedžio aukštis) dabartinio mazgo.
  • Jei balanso koeficientas didesnis nei 1, tada dabartinis mazgas yra nesubalansuotas ir mes esame arba Kairė Kairė dėklas arba kairysis Dešinysis dėklas . Norėdami patikrinti, ar yra kairėje pusėje ar ne, palyginkite naujai įdėtą raktą su raktu kairioji pomedžio šaknis .
  • Jei balanso koeficientas mažesnis nei -1 , tada dabartinis mazgas yra nesubalansuotas ir mes esame dešiniosios dešinės arba dešinės-kairės raidėmis. Norėdami patikrinti, ar tai yra dešinioji raidė, ar ne, palyginkite naujai įdėtą raktą su raktu dešinėje pomedžio šaknyje.

Toliau pateikiamas pirmiau minėto metodo įgyvendinimas:

C++14




// C++ program to insert a node in AVL tree> #include> using> namespace> std;> > // An AVL tree node> class> Node> {> >public>:> >int> key;> >Node *left;> >Node *right;> >int> height;> };> > // A utility function to get the> // height of the tree> int> height(Node *N)> {> >if> (N == NULL)> >return> 0;> >return> N->aukštis;>> > // A utility function to get maximum> // of two integers> int> max(>int> a,>int> b)> {> >return> (a>b)? a : b;>> > /* Helper function that allocates a> >new node with the given key and> >NULL left and right pointers. */> Node* newNode(>int> key)> {> >Node* node =>new> Node();> >node->raktas = raktas;>> node->kairėje = ​​NULL;>> node->dešinė = NULL;>> node->aukštis = 1;>>>// added at leaf> >return>(node);> }> > // A utility function to right> // rotate subtree rooted with y> // See the diagram given above.> Node *rightRotate(Node *y)> {> >Node *x = y->kairėje;>> Node *T2 = x->teisė;>> >// Perform rotation> >x->dešinė = y;>> y->kairė = T2;>> >// Update heights> >y->aukštis = max(aukštis(y->kairė),> >height(y->dešinėje)) + 1;>> x->aukštis = max(aukštis(x->kairė),> >height(x->dešinėje)) + 1;>> >// Return new root> >return> x;> }> > // A utility function to left> // rotate subtree rooted with x> // See the diagram given above.> Node *leftRotate(Node *x)> {> >Node *y = x->teisė;>> Node *T2 = y->kairėje;>> >// Perform rotation> >y->kairėje = ​​x;>> x->dešinė = T2;>> >// Update heights> >x->aukštis = max(aukštis(x->kairė),> >height(x->dešinėje)) + 1;>> y->aukštis = max(aukštis(y->kairė),> >height(y->dešinėje)) + 1;>> >// Return new root> >return> y;> }> > // Get Balance factor of node N> int> getBalance(Node *N)> {> >if> (N == NULL)> >return> 0;> >return> height(N->kairėje) - aukštis(N->dešinė);>> > // Recursive function to insert a key> // in the subtree rooted with node and> // returns the new root of the subtree.> Node* insert(Node* node,>int> key)> {> >/* 1. Perform the normal BST insertion */> >if> (node == NULL)> >return>(newNode(key));> > >if> (key key)> >node->kairysis = įterpti(mazgas->kairysis, raktas);>> else> if> (key>mazgas->raktas)>> node->dešinė = įterpti(mazgas->dešinėn, raktas);>> else> // Equal keys are not allowed in BST> >return> node;> > >/* 2. Update height of this ancestor node */> >node->aukštis = 1 + max(aukštis(mazgas->kairė),> >height(node->teisė));>> >/* 3. Get the balance factor of this ancestor> >node to check whether this node became> >unbalanced */> >int> balance = getBalance(node);> > >// If this node becomes unbalanced, then> >// there are 4 cases> > >// Left Left Case> >if> (balance>1 && klavišas kairysis -> klavišas)> >return> rightRotate(node);> > >// Right Right Case> >if> (balance node->dešinysis-> klavišas)>> return> leftRotate(node);> > >// Left Right Case> >if> (balance>1 && klavišas> mazgas->kairysis->raktas)> >{> >node->left = leftPasukti(mazgas->kairė);>> return> rightRotate(node);> >}> > >// Right Left Case> >if> (balance <-1 && key right->raktas)>> {> >node->dešinėn = dešinėnPasukti(mazgas->dešinėn);>> return> leftRotate(node);> >}> > >/* return the (unchanged) node pointer */> >return> node;> }> > // A utility function to print preorder> // traversal of the tree.> // The function also prints height> // of every node> void> preOrder(Node *root)> {> >if>(root != NULL)> >{> >cout ' '; preOrder(root->kairėje); preOrder(root->right); } } // Tvarkyklės kodas int main() { Mazgas *root = NULL; /* Konstravimo medis pateiktas aukščiau esančiame paveikslėlyje */ šaknis = insert(root, 10); šaknis = įterpti(šaknis, 20); šaknis = įterpti(šaknis, 30); šaknis = įterpti(šaknis, 40); šaknis = įterpti(šaknis, 50); šaknis = įterpti(šaknis, 25); /* Pastatytas AVL medis būtų 30 / 20 40 / 10 25 50 */ cout<< 'Preorder traversal of the ' 'constructed AVL tree is '; preOrder(root); return 0; } // This code is contributed by // rathbhupendra> 

>

>

C




// C program to insert a node in AVL tree> #include> #include> > // An AVL tree node> struct> Node> {> >int> key;> >struct> Node *left;> >struct> Node *right;> >int> height;> };> > // A utility function to get the height of the tree> int> height(>struct> Node *N)> {> >if> (N == NULL)> >return> 0;> >return> N->aukštis;>> > // A utility function to get maximum of two integers> int> max(>int> a,>int> b)> {> >return> (a>b)? a : b;>> > /* Helper function that allocates a new node with the given key and> >NULL left and right pointers. */> struct> Node* newNode(>int> key)> {> >struct> Node* node = (>struct> Node*)> >malloc>(>sizeof>(>struct> Node));> >node->raktas = raktas;>> node->kairėje = ​​NULL;>> node->dešinė = NULL;>> node->aukštis = 1;>>>return>(node);> }> > // A utility function to right rotate subtree rooted with y> // See the diagram given above.> struct> Node *rightRotate(>struct> Node *y)> {> >struct> Node *x = y->kairėje;>> struct> Node *T2 = x->teisė;>> >// Perform rotation> >x->dešinė = y;>> y->kairė = T2;>> >// Update heights> >y->aukštis = max(aukštis(y->kairė),> >height(y->dešinėje)) + 1;>> x->aukštis = max(aukštis(x->kairė),> >height(x->dešinėje)) + 1;>> >// Return new root> >return> x;> }> > // A utility function to left rotate subtree rooted with x> // See the diagram given above.> struct> Node *leftRotate(>struct> Node *x)> {> >struct> Node *y = x->teisė;>> struct> Node *T2 = y->kairėje;>> >// Perform rotation> >y->kairėje = ​​x;>> x->dešinė = T2;>> >// Update heights> >x->aukštis = max(aukštis(x->kairė),> >height(x->dešinėje)) + 1;>> y->aukštis = max(aukštis(y->kairė),> >height(y->dešinėje)) + 1;>> >// Return new root> >return> y;> }> > // Get Balance factor of node N> int> getBalance(>struct> Node *N)> {> >if> (N == NULL)> >return> 0;> >return> height(N->kairėje) - aukštis(N->dešinė);>> > // Recursive function to insert a key in the subtree rooted> // with node and returns the new root of the subtree.> struct> Node* insert(>struct> Node* node,>int> key)> {> >/* 1. Perform the normal BST insertion */> >if> (node == NULL)> >return>(newNode(key));> > >if> (key key)> >node->kairysis = įterpti(mazgas->kairysis, raktas);>> else> if> (key>mazgas->raktas)>> node->dešinė = įterpti(mazgas->dešinėn, raktas);>> else> // Equal keys are not allowed in BST> >return> node;> > >/* 2. Update height of this ancestor node */> >node->aukštis = 1 + max(aukštis(mazgas->kairė),> >height(node->teisė));>> >/* 3. Get the balance factor of this ancestor> >node to check whether this node became> >unbalanced */> >int> balance = getBalance(node);> > >// If this node becomes unbalanced, then> >// there are 4 cases> > >// Left Left Case> >if> (balance>1 && klavišas kairysis -> klavišas)> >return> rightRotate(node);> > >// Right Right Case> >if> (balance node->dešinysis-> klavišas)>> return> leftRotate(node);> > >// Left Right Case> >if> (balance>1 && klavišas> mazgas->kairysis->raktas)> >{> >node->left = leftPasukti(mazgas->kairė);>> return> rightRotate(node);> >}> > >// Right Left Case> >if> (balance <-1 && key right->raktas)>> {> >node->dešinėn = dešinėnPasukti(mazgas->dešinėn);>> return> leftRotate(node);> >}> > >/* return the (unchanged) node pointer */> >return> node;> }> > // A utility function to print preorder traversal> // of the tree.> // The function also prints height of every node> void> preOrder(>struct> Node *root)> {> >if>(root != NULL)> >{> >printf>(>'%d '>, root->Raktas);>> preOrder(root->kairėje);>> preOrder(root->teisė);>> }> }> > /* Driver program to test above function*/> int> main()> {> >struct> Node *root = NULL;> > >/* Constructing tree given in the above figure */> >root = insert(root, 10);> >root = insert(root, 20);> >root = insert(root, 30);> >root = insert(root, 40);> >root = insert(root, 50);> >root = insert(root, 25);> > >/* The constructed AVL Tree would be> >30> >/> >20 40> >/> >10 25 50> >*/> > >printf>(>'Preorder traversal of the constructed AVL'> >' tree is '>);> >preOrder(root);> > >return> 0;> }> 

>

>

Java




// Java program for insertion in AVL Tree> class> Node {> >int> key, height;> >Node left, right;> > >Node(>int> d) {> >key = d;> >height =>1>;> >}> }> > class> AVLTree {> > >Node root;> > >// A utility function to get the height of the tree> >int> height(Node N) {> >if> (N ==>null>)> >return> 0>;> > >return> N.height;> >}> > >// A utility function to get maximum of two integers> >int> max(>int> a,>int> b) {> >return> (a>b)? a : b;>> }> > >// A utility function to right rotate subtree rooted with y> >// See the diagram given above.> >Node rightRotate(Node y) {> >Node x = y.left;> >Node T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height = max(height(y.left), height(y.right)) +>1>;> >x.height = max(height(x.left), height(x.right)) +>1>;> > >// Return new root> >return> x;> >}> > >// A utility function to left rotate subtree rooted with x> >// See the diagram given above.> >Node leftRotate(Node x) {> >Node y = x.right;> >Node T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height = max(height(x.left), height(x.right)) +>1>;> >y.height = max(height(y.left), height(y.right)) +>1>;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >int> getBalance(Node N) {> >if> (N ==>null>)> >return> 0>;> > >return> height(N.left) - height(N.right);> >}> > >Node insert(Node node,>int> key) {> > >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)> >return> (>new> Node(key));> > >if> (key node.left = insert(node.left, key); else if (key>mazgas.raktas) mazgas.dešinė = įterpti(mazgas.dešinė, raktas); else // Dubliuoti raktai neleidžiami grąžinti mazgą; /* 2. Atnaujinkite šio pirmtako mazgo aukštį */ mazgas.height = 1 + max(height(mazgas.kairėje), aukštis(mazgas.dešinė)); /* 3. Gaukite šio pirmtako mazgo balanso koeficientą, kad patikrintumėte, ar šis mazgas nebuvo išbalansuotas */ int balance = getBalance(mazgas); // Jei šis mazgas tampa nesubalansuotas, yra // 4 atvejai Left Left Case if (balansas> 1 && klavišas return rightRotate(node); // Right Right Case if (balance<-1 && key>mazgas.dešinė.raktas) return leftPasukti(mazgas); // Kairėn dešiniosios raidės if (balansas> 1 && klavišas> mazgas.kairysis.key) { node.left = leftPasukti(mazgas.kairėje); grįžti į dešinęPasukti(mazgas); } // Dešinė kairioji raidė if (balansas<-1 && key node.right = rightRotate(node.right); return leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node void preOrder(Node node) { if (node != null) { System.out.print(node.key + ' '); preOrder(node.left); preOrder(node.right); } } public static void main(String[] args) { AVLTree tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ System.out.println('Preorder traversal' + ' of constructed tree is : '); tree.preOrder(tree.root); } } // This code has been contributed by Mayank Jaiswal> 

>

>

Python3




# Python code to insert a node in AVL tree> > # Generic tree node class> class> TreeNode(>object>):> >def> __init__(>self>, val):> >self>.val>=> val> >self>.left>=> None> >self>.right>=> None> >self>.height>=> 1> > # AVL tree class which supports the> # Insert operation> class> AVL_Tree(>object>):> > ># Recursive function to insert key in> ># subtree rooted with node and returns> ># new root of subtree.> >def> insert(>self>, root, key):> > ># Step 1 - Perform normal BST> >if> not> root:> >return> TreeNode(key)> >elif> key root.left = self.insert(root.left, key) else: root.right = self.insert(root.right, key) # Step 2 - Update the height of the # ancestor node root.height = 1 + max(self.getHeight(root.left), self.getHeight(root.right)) # Step 3 - Get the balance factor balance = self.getBalance(root) # Step 4 - If the node is unbalanced, # then try out the 4 cases # Case 1 - Left Left if balance>1 ir raktas grąžina save.rightRotate(root) # 2 atvejis – dešinėn, jei balansas<-1 and key>root.right.val: return self.leftRotate(root) # 3 atvejis – kairėn dešinėn, jei balansas> 1 ir raktas> root.left.val: root.left = self.leftRotate(root.left) return self.rightRotate(root) ) # 4 atvejis – dešinė Kairė, jei balansas<-1 and key root.right = self.rightRotate(root.right) return self.leftRotate(root) return root def leftRotate(self, z): y = z.right T2 = y.left # Perform rotation y.left = z z.right = T2 # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right)) # Return the new root return y def rightRotate(self, z): y = z.left T3 = y.right # Perform rotation y.right = z z.left = T3 # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right)) # Return the new root return y def getHeight(self, root): if not root: return 0 return root.height def getBalance(self, root): if not root: return 0 return self.getHeight(root.left) - self.getHeight(root.right) def preOrder(self, root): if not root: return print('{0} '.format(root.val), end='') self.preOrder(root.left) self.preOrder(root.right) # Driver program to test above function myTree = AVL_Tree() root = None root = myTree.insert(root, 10) root = myTree.insert(root, 20) root = myTree.insert(root, 30) root = myTree.insert(root, 40) root = myTree.insert(root, 50) root = myTree.insert(root, 25) '''The constructed AVL Tree would be 30 / 20 40 / 10 25 50''' # Preorder Traversal print('Preorder traversal of the', 'constructed AVL tree is') myTree.preOrder(root) print() # This code is contributed by Ajitesh Pathak> 

>

>

C#




// C# program for insertion in AVL Tree> using> System;> > class> Node> {> >public> int> key, height;> >public> Node left, right;> > >public> Node(>int> d)> >{> >key = d;> >height = 1;> >}> }> > public> class> AVLTree> {> > >Node root;> > >// A utility function to get> >// the height of the tree> >int> height(Node N)> >{> >if> (N ==>null>)> >return> 0;> > >return> N.height;> >}> > >// A utility function to get> >// maximum of two integers> >int> max(>int> a,>int> b)> >{> >return> (a>b)? a : b;>> }> > >// A utility function to right> >// rotate subtree rooted with y> >// See the diagram given above.> >Node rightRotate(Node y)> >{> >Node x = y.left;> >Node T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height = max(height(y.left),> >height(y.right)) + 1;> >x.height = max(height(x.left),> >height(x.right)) + 1;> > >// Return new root> >return> x;> >}> > >// A utility function to left> >// rotate subtree rooted with x> >// See the diagram given above.> >Node leftRotate(Node x)> >{> >Node y = x.right;> >Node T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height = max(height(x.left),> >height(x.right)) + 1;> >y.height = max(height(y.left),> >height(y.right)) + 1;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >int> getBalance(Node N)> >{> >if> (N ==>null>)> >return> 0;> > >return> height(N.left) - height(N.right);> >}> > >Node insert(Node node,>int> key)> >{> > >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)> >return> (>new> Node(key));> > >if> (key node.left = insert(node.left, key); else if (key>mazgas.raktas) mazgas.dešinė = įterpti(mazgas.dešinė, raktas); else // Dubliuoti raktai neleidžiami grąžinti mazgą; /* 2. Atnaujinkite šio pirmtako mazgo aukštį */ mazgas.height = 1 + max(height(mazgas.kairėje), aukštis(mazgas.dešinė)); /* 3. Gaukite šio pirmtako mazgo balanso koeficientą, kad patikrintumėte, ar šis mazgas nebuvo išbalansuotas */ int balance = getBalance(mazgas); // Jei šis mazgas tampa nesubalansuotas, yra // 4 atvejai Left Left Case if (balansas> 1 && klavišas return rightRotate(node); // Right Right Case if (balance node.right.key) return leftRotate(node) ; // Left Right Case if (balance> 1 && key> node.left.key) { node.left = leftPasukti(mazgas.left) // Right Left Case if (balansas);<-1 && key < node.right.key) { node.right = rightRotate(node.right); return leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node void preOrder(Node node) { if (node != null) { Console.Write(node.key + ' '); preOrder(node.left); preOrder(node.right); } } // Driver code public static void Main(String[] args) { AVLTree tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ Console.Write('Preorder traversal' + ' of constructed tree is : '); tree.preOrder(tree.root); } } // This code has been contributed // by PrinciRaj1992> 

>

>

Javascript




> > >// JavaScript program for insertion in AVL Tree> >class Node {> >constructor(d) {> >this>.key = d;> >this>.height = 1;> >this>.left =>null>;> >this>.right =>null>;> >}> >}> > >class AVLTree {> >constructor() {> >this>.root =>null>;> >}> > >// A utility function to get> >// the height of the tree> >height(N) {> >if> (N ==>null>)>return> 0;> > >return> N.height;> >}> > >// A utility function to get> >// maximum of two integers> >max(a, b) {> >return> a>b ? a : b;>> }> > >// A utility function to right> >// rotate subtree rooted with y> >// See the diagram given above.> >rightRotate(y) {> >var> x = y.left;> >var> T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height =>this>.max(>this>.height(y.left),> >this>.height(y.right)) + 1;> >x.height =>this>.max(>this>.height(x.left),> >this>.height(x.right)) + 1;> > >// Return new root> >return> x;> >}> > >// A utility function to left> >// rotate subtree rooted with x> >// See the diagram given above.> >leftRotate(x) {> >var> y = x.right;> >var> T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height =>this>.max(>this>.height(x.left),> >this>.height(x.right)) + 1;> >y.height =>this>.max(>this>.height(y.left),> >this>.height(y.right)) + 1;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >getBalance(N) {> >if> (N ==>null>)>return> 0;> > >return> this>.height(N.left) ->this>.height(N.right);> >}> > >insert(node, key) {> >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)>return> new> Node(key);> > >if> (key node.left = this.insert(node.left, key); else if (key>mazgas.raktas) mazgas.dešinė = this.insert(mazgas.dešinė, raktas); // Dubliuoti raktai neleidžiami, kitaip grąžinamas mazgas; /* 2. Atnaujinkite šio pirmtako mazgo aukštį */ mazgas.height = 1 + this.max(this.height(mazgas.left), this.height(mazgas.dešinė)); /* 3. Gaukite šio pirmtako mazgo balanso koeficientą, kad patikrintumėte, ar šis mazgas nebuvo išbalansuotas */ var balance = this.getBalance(node); // Jei šis mazgas tampa nesubalansuotas, yra // 4 atvejai Left Left Case if (balansas> 1 && klavišas grąžina this.rightRotate(node); // Dešinė dešinė Case if (balance node.right.key) grąžina tai. leftRotate(mazgas); // Left Right Case if (balance> 1 && key> node.left.key) { node.left = this.leftRotate(node.left) return this.right(mazgas); Kairioji raidė, jei (balansas<-1 && key < node.right.key) { node.right = this.rightRotate(node.right); return this.leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node preOrder(node) { if (node != null) { document.write(node.key + ' '); this.preOrder(node.left); this.preOrder(node.right); } } } // Driver code var tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ document.write( 'Preorder traversal of the ' + 'constructed AVL tree is ' ); tree.preOrder(tree.root);> 

>

>

Išvestis 

Preorder traversal of the constructed AVL tree is 30 20 10 25 40 50>

Sudėtingumo analizė

Laiko sudėtingumas: O(log(n)), Įterpimui
Pagalbinė erdvė: O(1)

nelygus taškas

Sukimo operacijos (sukimas į kairę ir į dešinę) trunka pastoviai, nes ten pakeičiamos tik kelios rodyklės. Ūgiui atnaujinti ir balanso koeficientui gauti taip pat reikia pastovaus laiko. Taigi AVL intarpo laiko sudėtingumas išlieka toks pat kaip ir BST įdėklo, kuris yra O (h), kur h yra medžio aukštis. Kadangi AVL medis yra subalansuotas, aukštis yra O (Logn). Taigi AVL įterpimo laiko sudėtingumas yra O (Logn).

Palyginimas su raudonu juodu medžiu:

AVL medis ir kiti savaiminio balansavimo paieškos medžiai, tokie kaip raudona juoda, yra naudingi norint atlikti visas pagrindines operacijas per O (log n) laiką. AVL medžiai yra labiau subalansuoti, palyginti su raudonai juodais medžiais, tačiau įterpiant ir ištrinant jie gali sukelti daugiau apsisukimų. Taigi, jei jūsų programa apima daug dažnų įterpimų ir trynimų, pirmenybė turėtų būti teikiama raudonai juodiems medžiams. Ir jei įterpimai ir ištrynimai atliekami rečiau, o paieška atliekama dažniau, pirmenybė turėtų būti teikiama AVL medžiui, o ne Red Black Tree .

Toliau pateikiamas įrašas, skirtas ištrinti AVL medyje:
AVL medis | 2 rinkinys (ištrynimas)