Atsižvelgiant į a BST , užduotis yra ieškoti mazgo šiame BST .

Norėdami ieškoti vertės BST, laikykite ją surūšiuotu masyvu. Dabar galime lengvai atlikti paieškos operaciją BST naudodami Dvejetainės paieškos algoritmas .

Algoritmas ieškant rakto tam tikrame dvejetainiame paieškos medyje:

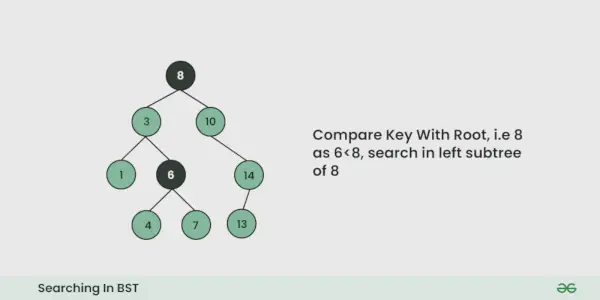
Tarkime, kad norime ieškoti numerio X, Mes pradedame nuo šaknų. Tada:

• Ieškomą reikšmę lyginame su šaknies reikšme.
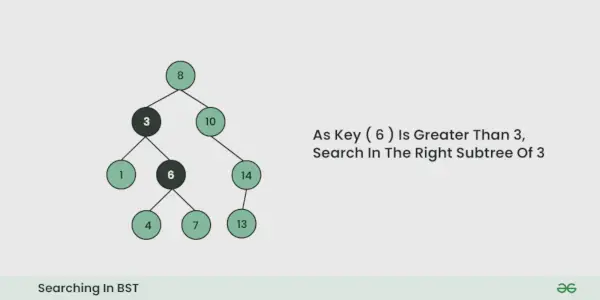
  • Jei jis lygus, mes baigiame paiešką, jei jis mažesnis, žinome, kad turime eiti į kairįjį pomedį, nes dvejetainiame paieškos medyje visi kairiojo pomedžio elementai yra mažesni, o visi dešiniojo pomedžio elementai yra didesni.
• Kartokite aukščiau aprašytą veiksmą, kol nebebus įmanoma pereiti
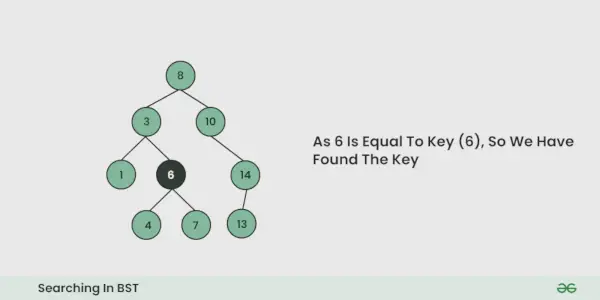
• Jei bet kurios iteracijos metu randamas raktas, grąžinkite True. Kitaip netiesa.

Paieškos BST iliustracija:

Norėdami geriau suprasti, žiūrėkite toliau pateiktą iliustraciją:

Programa paieškai įgyvendinti BST:

C++

>

>

C

intellij idėja vs užtemimas

>

>

Java

> 
    
   
 
     
  
 
    
 
     
     
    
 
 
 
 
 
 # Python3 function to search a given key in a given BST> class> Node:> ># Constructor to create a new node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # A utility function to insert> # a new node with the given key in BST> def> insert(node, key):> ># If the tree is empty, return a new node> >if> node>is> None>:> >return> Node(key)> ># Otherwise, recur down the tree> >if> key   node.left = insert(node.left, key)  elif key>node.key: node.right = insert(mazgas.dešinė, raktas) # Grąžinti (nepakeistą) mazgo rodyklės grąžinimo mazgą # Naudingumo funkcija, skirta ieškoti rakto BST def paieškoje (šaknis, raktas): # Pagrindiniai atvejai: šaknis yra Nulis arba raktas yra šaknyje, jei root yra None arba root.key == raktas: return root # Raktas yra didesnis nei root's key if root.key return search(root.right, key) # Raktas mažesnis nei root 's key return search(root.left, key) # Tvarkyklės kodas if __name__ == '__main__': root = Nėra root = įterpti(šaknis, 50) įterpti(šaknis, 30) įterpti(šaknis, 20) įterpti (šaknis, 40) įterpti(šaknis, 70) įterpti(šaknis, 60) įterpti(šaknis, 80) # Raktas raktas = 6 # Ieškant BST, jei paieška(šaknis, raktas) yra None: print(key, 'nerasta') else: print(raktas, 'rastas') raktas = 60 # Ieškoma BST, jei paieška (šaknis, raktas) yra Nėra: print(raktas, 'nerasta') kita: print(raktas, 'rasta')>
 
 
 
 
    
 
>
 
    
 
>
 
 
C#
    
 
     
  
 
    
 
     
     
    
 
 
 
 
 
 // C# function to search a given key in a given BST> using> System;> public> class> Node {> >public> int> key;> >public> Node left, right;> }> public> class> BinaryTree {> >// A utility function to create a new BST node> >public> Node NewNode(>int> item)> >{> >Node temp =>new> Node();> >temp.key = item;> >temp.left = temp.right =>null>;> >return> temp;> >}> >// A utility function to insert> >// a new node with given key in BST> >public> Node Insert(Node node,>int> key)> >{> >// If the tree is empty, return a new node> >if> (node ==>null>)> >return> NewNode(key);> >// Otherwise, recur down the tree> >if> (key   node.left = Insert(node.left, key);  else if (key>mazgas.raktas) node.right = Įterpti(mazgas.dešinė, raktas);  // Grąžinti (nepakeistą) mazgo rodyklę return node;  } // Naudingumo funkcija ieškoti rakto BST viešajame mazgo paieškoje (mazgo šaknis, int raktas) // Pagrindiniai atvejai: root yra nulis arba raktas yra šaknyje if (root == null // Tvarkyklės kodas public static void Pagrindinis () { Mazgas šaknis = null; , 40; bt.Insert(root, 60); bt.Search(root, key) == null) Console.WriteLine(key + ' not found'); else Console.WriteLine(key + ' key = 60); if (bt.Search(root, key) == null) Console.WriteLine(key + ' not found'); else Console.WriteLine(key + ' found' } }>'>);
 
 
 
 
    
 
> 
    
   
 
     
  
 
    
 
     
     
    
 
 
 
 
 
 // Javascript function to search a given key in a given BST> class Node {> >constructor(key) {> >this>.key = key;> >this>.left =>null>;> >this>.right =>null>;> >}> }> // A utility function to insert> // a new node with given key in BST> function> insert(node, key) {> >// If the tree is empty, return a new node> >if> (node ===>null>) {> >return> new> Node(key);> >}> >// Otherwise, recur down the tree> >if> (key   node.left = insert(node.left, key);  } else if (key>mazgas.raktas) { mazgas.dešinė = įterpti(mazgas.dešinė, raktas);  } // Grąžina (nepakeistą) mazgo rodyklės grąžinimo mazgą; } // Naudingumo funkcija, skirta ieškoti rakto BST funkcijos paieškoje (šaknis, raktas) { // Pagrindiniai atvejai: šaknis yra nulis arba raktas yra šaknyje if (root === null || root.key === raktas ) { grąžinti šaknį;  } // Raktas yra didesnis nei šakninis raktas if (root.key return search(root.right, key); } // Raktas yra mažesnis už root's key return search(root.left, key); } // Tvarkyklės kodas tegul root = įterpti(root, 30) įterpti(root, 70); 60); rasti');} else { console.log(key + ' found' } key = 60) // Ieškoma BST if (search(root, key) === null) { console.log(; klavišas + ' nerastas'); } else { console.log(key + ' found' }>'>);
 
 
 
 
    
 
> 
    
 6 not found 60 found>
 
    Laiko sudėtingumas:    O(h), kur h yra BST aukštis.  
    Pagalbinė erdvė:    O(h), kur h yra BST aukštis. Taip yra todėl, kad maksimalus vietos kiekis, reikalingas rekursijos kamino saugojimui, būtų    h    .
 
    Susijusios nuorodos:     
 
 
  Dvejetainės paieškos medžio įterpimo operacija  
 
 Dvejetainės paieškos medžio ištrynimo operacija