logo

TechCodeview

Ploto formulės

Ploto formulės įvairiems objektams yra formulės, kurios naudojamos įvairių objektų plotui rasti. Plotas yra erdvė, kurią užima bet kurios figūros riba. Įvairių geometrinių formų plotų formulės priklauso nuo įvairių parametrų, tokių kaip įvairių geometrinių formų matmenys, aukštis ir spindulys. Geometrinės formos yra dviejų tipų:

  • Dvimatės formos (dvimatės formos)
  • Trimatės formos (3-D formos)

Šiame straipsnyje mes išsamiai sužinosime apie įvairių 2-D ir 3-D formų plotų formules, tokias kaip stačiakampio plotas, kvadrato plotas, apskritimo plotas, kubo plotas ir kt.



Turinys

Kas yra Plotas?

Erdvė, kurią užima figūros riba, vadinama figūros plotu. Jis matuojamas kvadrato vienetu. SI vienetas plotui matuoti yra m2. Plotas naudojamas įvairiose matematinėse sąvokose, taip pat naudojamas realiame gyvenime, pavyzdžiui, norint rasti kambario plotą, ploto lentelę ir kt.

Kas yra ploto formulės?

Ploto formulės yra esminiai įrankiai, naudojami matematikoje, norint apskaičiuoti skirtingų dvimačių formų uždarytos erdvės kiekį. Šios formulės gali būti naudojamos geometriniam plotui rasti figūros, tokios kaip kvadratai, stačiakampiai, apskritimai, trikampiai, trapecijos ir elipsės. Naudodami šias formules galime tiksliai apskaičiuoti skirtingų formų plotą, leidžiantį išspręsti realaus pasaulio problemas ir atlikti svarbius skaičiavimus.



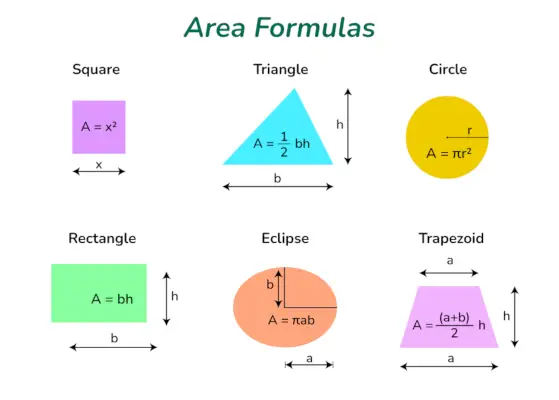
Plotas-Formulės

Ploto formulės

Kas yra 2D formos?

Formos, turinčios tik du matmenis, vadinamos 2-D formos . Jie nupiešti 2-D erdvėje ir priklauso nuo 2 parametrai, paprastai ilgis (l) ir plotis (b). Įvairios 2-D formos yra Stačiakampis, kvadratas, trikampis, apskritimai ir kt.

2D formų formulės sritis

2D formų ploto formulės yra formulės, kurios naudojamos norint pamėgti įvairių 2D formų plotus, pvz., trikampio plotą, kvadrato plotą, stačiakampio plotą, rombo plotą ir kt. Šios plotų formulės yra labai naudojamos matematikoje spręsti įvairius geometrinius uždavinius. Įvairios įvairių formų plotų formulės yra,



Stačiakampio ploto formulė

Stačiakampis yra dvimatė figūra kuris yra keturkampis, t.y. turi keturios pusės jo priešingos pusės yra lygiagrečios ir lygios. Visi stačiakampio kampai yra lygūs, o jų matas yra 90 laipsnių. Stačiakampio įstrižainės yra lygios ir yra statmenos viena kitai.

Stačiakampio ploto apskaičiavimo formulė yra su ilgiu ir l ir plotis b yra,

  • Stačiakampio plotas (A) = l×b kvadratiniai vienetai

Kvadrato ploto formulė

Kvadratas yra dvimatė figūra, kuri yra keturkampė, ty turi keturias kraštines, jos priešingos kraštinės yra lygiagrečios, o visos keturios kvadrato kraštinės yra lygios. Visi kvadrato kampai yra lygūs, o jų matas yra 90 laipsnių. Kvadrato įstrižainės yra lygios ir yra statmenos viena kitai.

Kvadrato su kraštine ploto apskaičiavimo formulė a yra,

  • Kvadrato plotas (A) = a 2 kv.vnt

Trikampio ploto formulė

Trikampis yra paprasčiausias daugiakampis, sudarytas sujungiant tris tiesias linijas. Kaip rodo pavadinimas, tai daugiakampis su trimis kampais. Visų trikampio kraštinių ilgių suma yra trikampio perimetras, o erdvė trikampio perimetro viduje yra trikampio plotas.

modifikavimo klavišai

Formulė trikampio su pagrindu plotui apskaičiuoti b yra ir aukštis h yra,

  • Trikampio plotas (A) = 1/2 × bh kv.vnt

Apskritimo ploto formulė

Apskritimas yra geometrinė figūra be tiesios linijos. Tai taško lokusas, kuris visada yra pastoviu atstumu nuo fiksuoto taško. Fiksuotas taškas vadinamas apskritimo centru, o fiksuotas atstumas yra apskritimo spindulys.

Apskaičiavimo formulė apskritimo plotas kai r yra apskritimo spindulys,

  • Apskritimo plotas (A) = πr 2 kv.vnt

Lygiagretainio ploto formulė

Lygiagretė yra dvimatė figūra kurioje priešingos kraštinės lygiagrečios ir lygios. Lygiagretainio su pagrindu ploto apskaičiavimo formulė b ir aukščio h yra,

  • Lygiagretainio plotas (A) = bh kv. vnt

Rombo ploto formulė

Rombas yra keturkampis, kurio visos keturios kraštinės yra lygios ir lygiagrečios, bet ne visi kampai yra lygūs. Rombo ploto su įstriža apskaičiavimo formulė d 1 ir d 2 yra,

  • Rombo plotas (A) = 1/2 × d 1 × d 2 kv.vnt

Trapecijos ploto formulė

Trapecija yra kitas pavadinimas trapecija . Tai keturkampis, kurio priešingos kraštinės yra lygiagrečios. Trapecijos su lygiagrečiomis kraštinėmis ploto apskaičiavimo formulė a ir b ir aukščio h yra,

  • Trapecijos plotas (A) = 1/2(a +b)h kv.vnt

Elipsės ploto formulė

Elipsė yra 2-D forma ir susideda iš kūginių dalių. Elipsės su ašimi as ploto apskaičiavimo formulė a ir b yra,

  • Elipsės plotas (A) = πab kv.vnt

Puslankio ploto formulė

Puslankis yra dvimatė figūra, kuri yra pusė apskritimo. Puslankio su spinduliu r ploto apskaičiavimo formulė yra

  • Puslankio plotas (A) = 1/4(πr 2 ) kv.vnt

Ploto formulių lentelė

Įvairių dvimačių figūrų plotų formulės įtrauktos į toliau pateiktą lentelę,

Figūros

Formulė

Kintamieji

Stačiakampis

Plotas = l×b
  • l yra ilgis
  • b yra plotis

Kvadratas

Plotas = a2

a yra kvadrato kraštinė

Trikampis

Plotas = 1/2 × bh
  • b yra pagrindas
  • h yra aukštis

Apskritimas

Plotas = πr2

r yra apskritimo spindulys

Trapecija

Plotas = 1/2×(a+b)h
  • a yra pirmoji bazė
  • b yra antrasis pagrindas

Rombas

Plotas = 1/2×d1×d2
  • d1yra viena įstrižainė
  • d2yra antroji įstrižainė

Lygiagretainis

Plotas = b × h
  • b yra pagrindas
  • h yra aukštis

Elipsė

Plotas = πab
  • a yra pagrindinės ašies spindulys
  • b yra mažosios ašies spindulys

Kas yra 3D formos?

3-D formos yra figūros, nubrėžtos 3-D erdvėse. Jie turi 3 matmenis, kurie yra jų parametrai. Šių formų plotas priklauso nuo 3D formų ilgio, pločio ir aukščio. Įvairios 3-D formos yra kubas, kubas, cilindras, kūgis, rutulys ir kt. 3D formų plotas yra dviejų kategorijų: išlenkto paviršiaus plotas (šoninis paviršiaus plotas) {CSA} ir bendras paviršiaus plotas (TSA). CSA yra visų 3D formų išlenkto paviršiaus plotas, o TSA yra visų 3D formų paviršių plotas.

3D formų formulės sritis

3-D formų plotas yra erdvė, kurią užima visi figūros veidai. Jis matuojamas vienetais2. SI ploto vienetas yra m2. The kubo plotas , stačiakampio plotas , cilindro plotas, kūgio plotas ir kiti yra 3D formų srityje. Toliau pateiktoje lentelėje parodytos įvairių 3-D figūrų formulės.

Formos sritis

Paviršiaus plotas

Parametrai

Kubo plotas

6a2

a yra krašto ilgis

Kuboido sritis

2 (lb + lh + bh)
  • l yra krašto ilgis
  • b yra krašto plotis
  • h yra krašto aukštis

Kūgio plotas

πr(r + l)
  • r = apskritimo pagrindo spindulys
  • l = nuožulnus aukštis

Cilindro plotas

2π(r + h)
  • r = apskritimo pagrindo spindulys
  • h = cilindro aukštis

Sferos sritis

4πr2

r yra sferos spindulys

Pusrutulio sritis

3πr2

r yra pusrutulio spindulys

Stačiakampės prizmės plotas

2 (wl + hl + hw)
  • l yra krašto ilgis
  • w yra krašto plotis
  • h yra krašto aukštis

Taip pat patikrinkite

  • Ploto ir perimetro formulės
  • Paviršiaus ploto formulės

Ploto formulių pavyzdžiai

1 pavyzdys: Raskite stačiakampio, kurio ilgis 5 cm ir plotis 2 cm, plotą.

Sprendimas:

faktorialas java

Atsižvelgiant į

  • Stačiakampio ilgis (l) = 5 cm
  • Stačiakampio plotis (b) = 2 cm

Stačiakampio (A) plotas = l × b

A = 5 cm × 2 cm
= 10 cm2

2 pavyzdys: Raskite kvadratinio parko plotą, kurio kraštinė yra 4 m.

Sprendimas:

Atsižvelgiant į

  • Kvadrato (a) kraštinė = 4 m

Kvadrato plotas = a2
= (4)2= 16 m2

Taigi aikštės parko plotas siekia 16 m2

3 pavyzdys: Raskite trikampės plokštės, kurios aukštis yra 6 cm, o pagrindas yra 6 cm, plotą.

Sprendimas:

Atsižvelgiant į

  • Trikampio aukštis (h) = 6 cm
  • Trikampio (b) pagrindas = 8 cm

Trikampio plotas (A) = 1/2 (b × h)

A = 1/2 (8 × 6)
= 48/2 = 24 cm2

np.random.rand

Trikampės plokštės plotas 24 cm2

4 pavyzdys: Raskite apskrito disko plotą, kurio spindulys yra 1,4 cm.

Sprendimas:

Atsižvelgiant į

  • Apskritimo spindulys (r) = 1,4 cm

Apskritimo plotas(A) = πr2

A = π(1,4)2
= 22/7 (1,4) (1,4) = (4,4) (1,4)
= 6,16 cm2

Apvalaus disko plotas 6,16 cm2

Sritys formulių DUK

Kas yra ploto formulės?

Ploto formulės yra formulės, naudojamos bet kurios figūros plotui rasti. Jis naudojamas norint nustatyti, kiek vietos užima figūra. Paprastai sritis vaizduojama raide „A“. ir matuojamas vienetais2, t.y. cm2, m2ir kt.

Kas yra aikštės formulė?

Kvadrato ploto formulė yra kvadrato užimamos erdvės skaičiavimo formulė. Formulė kvadrato plotui apskaičiuoti yra tokia:

Kvadrato plotas = (pusė) 2

Kas yra stačiakampio ploto formulė?

Stačiakampio ploto formulė yra formulė, skirta apskaičiuoti stačiakampio užimamą erdvę. Stačiakampio ploto apskaičiavimo formulė yra tokia:

Stačiakampio plotas = ilgis × plotis

Kas yra trikampio ploto formulė?

Trikampio ploto formulė yra formulė, skirta apskaičiuoti trikampio užimamą erdvę. Formulė trikampio plotui apskaičiuoti yra tokia:

Trikampio plotas = 1/2 (pagrindas × aukštis)

Kas yra apskritimo ploto formulė?

Apskritimo ploto formulė yra formulė, skirta apskaičiuoti apskritimo užimamą erdvę. Apskritimo ploto apskaičiavimo formulė yra tokia:

Apskritimo plotas = π(spindulys) 2

Kas yra keturkampio ploto formulė?

Keturkampio ploto apskaičiavimo formulė,

Keturkampio plotas = 1/2 × įstrižainė 1 × Įstrižainė 2

Kas yra trikampės prizmės ploto formulė?

Trikampės prizmės ploto formulė yra

Trikampės prizmės plotas = (pagrindo perimetras × prizmės ilgis) + 2 × pagrindo plotas

Kas yra daugiakampio ploto formulė?

Daugiakampio ploto apskaičiavimo formulė yra tokia:

Daugiakampio plotas = 1/2 × (perimetras × apotema)

Kas yra stačiojo trikampio ploto formulė?

Stačiojo kampo trikampio ploto formulė yra

Stačiojo trikampio plotas = 1/2 × statmenas × pagrindas

Kas yra Pentagono ploto formulė?

Pentagono ploto formulė yra

Pentagono plotas = 1/2 × perimetras × apotemas