Trapecija matematikoje: Trapecija yra daugiakampis su keturiomis kraštinėmis, t. y. jis yra keturkampis. Trapecija kilusi iš graikų kalbos žodžio trapeze, kuris reiškia stalą. Tai sudėtingas keturkampis. Trapecija yra specialus keturkampis, turintis tik vieną porą lygiagrečių kraštinių. Trapecija yra dvimatė forma, kuri atrodo kaip lentelė.
Trapecija turi keturias kraštines ir keturias viršūnes. Trapecijos formą matome kasdieniame gyvenime ir tai yra viena iš labiausiai paplitusių formų. Šiame straipsnyje mes sužinosime apie kas yra trapecija matematikoje, jos savybės, formulės, pavyzdžiai ir trapecijos tipai, kartu su kai kuriais išspręstais jos pavyzdžiais.
Turinys
- Kas yra trapecija matematikoje?
- Trapecijos tipai
- Netaisyklinga trapecija
- Trapecijos savybės
- Trapecijos formulė
- Trapecijos formulės sritis
- Trapecijos formulės perimetras
- Skirtumas tarp trapecijos ir trapecijos
- Trapecijos kampai
- Trapecijos įstrižainė
- Trapecijos pavyzdžiai
Kas yra trapecija matematikoje?
Trapecija yra uždaros formos dvimatis keturkampis, turintis porą lygiagrečių priešingų kraštinių. Lygiagrečios trapecijos kraštinės vadinamos bazėmis, o nelygiagrečios trapecijos kraštinės – kojomis. Trapecija turi keturias puses ir keturis kampus. A lygiagretainis dar vadinama trapecija su dviem lygiagrečiomis kraštinėmis.
Trapecijos apibrėžimas
Trapecija yra keturkampis (keturkampis daugiakampis), turintis bent vieną lygiagrečių kraštinių porą. Šios lygiagrečios kraštinės vadinamos trapecijos pagrindais, o kitos dvi kraštinės – kojelėmis, kurios nebūtinai yra lygiagrečios.
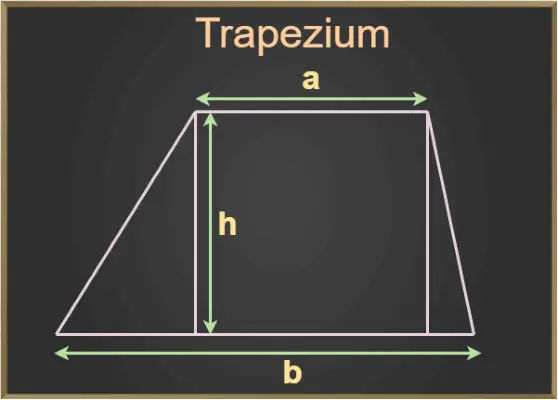
Aukščiau pateiktame paveikslėlyje a ir b yra trapecijos pagrindai, o h yra trapecijos aukštis.
Trapecijos forma
Trapecija yra a keturkampis y., daugiakampis su keturiomis kraštinėmis. Trapecija turi keturias puses su pora priešingų kraštų, lygiagrečių viena kitai. Trapecijos forma yra labai paplitusi, o kasdieniame gyvenime matome įvairių dalykų, panašių į trapeciją. Kai kurie mūsų pastebėti gyvenimiški trapecijos pavyzdžiai yra trapecijos formos stalai, plytelės, paveikslai ir kt.
Trapecijos tipai
Pagal šonus ir kampus trapecija yra trijų tipų:
- Scalene trapecija
- Lygiašonis trapecija
- Dešinė trapecija

Lygiašonis trapecija
Trapecija, kurios kojos yra vienodo ilgio, vadinamos lygiašone trapecija, t. y. lygiašone trapecija dvi nelygiagrečios kraštinės yra lygios.
Scalene trapecija
Trapecija, kurios visos kraštinės nėra lygios, vadinama skalenine trapecija. Skaleno trapecijoje nėra dviejų vienodų kampų.
Dešinė trapecija
Trapecija, turinti stačiojo kampo porą, greta viena kitos, vadinama stačia trapecija.
Netaisyklinga trapecija
Trapecija turi vieną porą lygiagrečių kraštinių, o kitos dvi kraštinės yra nelygiagrečios. Taisyklingoje trapecijoje kitos dvi nelygiagrečios kraštinės yra lygios, bet netaisyklingos trapecijos atveju dvi nelygiagrečios priešingos kraštinės yra nelygios.
Trapecijos savybės
Yra įvairių trapecijos savybių, kai kurios iš jų yra šios:
- Lygiagrečios pusės: Trapecija turi dvi lygiagrečias kraštines, kurios vadinamos bazėmis. Pavyzdys: AB ir CD pusės yra lygiagrečios viena kitai, parodyta paveikslėlyje.
- Nelygiagrečios pusės: Nelygiagrečios trapecijos kraštinės vadinamos kojomis, o trapecijos kojos nėra vienodo ilgio. Pavyzdys: Kraštinės AD ir BC yra nelygiagrečios trapecijos kraštinės.
- Aukštis arba aukštis virš jūros lygio: Statmenas atstumas tarp pagrindų vadinamas trapecijos aukščiu arba aukščiu. Aukščiau pateiktoje diagramoje h yra trapecijos aukštis.
- Kampų suma
- Gretimi vidiniai kampai trapecijoje sumuojami iki 180°. Pavyzdys: Yra dvi poros bendrų vidinių kampų. Viena pora yra ∠ A ir ∠ D, o kita pora yra ∠ B ir ∠ C. Kiekvienos bendrų vidinių kampų poros suma yra 180°.
- Visų trapecijos vidinių kampų suma visada yra 360°. Pavyzdys : Paveiksle ∠A+∠D yra 180°, o ∠B+∠C yra 180°. Todėl ∠A+∠D +∠B+∠C = 360°.
- Mediana: Trapecijos mediana yra linijos atkarpa, jungianti kojų vidurio taškus. Mediana lygiagreti pagrindams, o jos ilgis yra pagrindų ilgių vidurkis.
- Trapecija turi lygiai vieną porą priešingų lygiagrečių kraštinių.
Trapecijos formulė
Svarbios trapecijos formulės yra šios:
- Trapecijos sritis = ½ (lygiagrečių kraštinių suma) × (atstumas tarp lygiagrečių kraštų)
- Trapecijos perimetras = Visų keturių pusių suma
Trapecijos formulės sritis
Trapecija turi dvi lygiagrečias kraštines a ir b vienetus, o jos aukštis yra h.
Dabar trapecijos plotą galima apskaičiuoti suradus bazių vidurkį ir jo rezultatą padauginus iš aukščio. Vadinasi,
Trapecijos sritis = ((a +b)/2) × h
kur,
- a ir b yra trapecijos bazės
- h yra Aukštis
Lygiašonis trapecijos plotas
Tegu a ir b yra lygiagrečių trapecijos ABCD kraštinių ilgis, kur a ir b yra trapecijos pagrindai ir a>b.
Dabar, kadangi tai lygiašonė trapecija, c yra abiejų nelygiagrečių kraštinių ilgis, o h yra trapecijos aukštis.
Dabar AB = a, CD = b, BC = AD = c
Į Taisyklingas trikampis , AED
Statmens ilgis, h = √(c 2 – (a–b) 2 ) [naudojant Pitagoro teorema ]….(1)
Dabar
Plotas = ½ × lygiagrečių kraštinių suma × trapecijos aukštis
Plotas = ½ × (a+b) × h
Naudojant (1) lygtį
Lygiašonis trapecijos plotas = 1/2 × [√(c 2 – (a–b) 2 ) (a+b)]
Trapecijos formulės perimetras
Trapecijos perimetras gaunamas apskaičiuojant visų jos kraštinių sumą. Vadinasi,
Trapecijos perimetras = AB + BC + CD + AD
kur, AB, BC, CD ir REKLAMA yra Trapecijos pusės
Lygiašonės trapecijos perimetras
Jei lygiašonėje trapecijoje a ir b yra lygiagrečių kraštinių ilgiai, t. y. pagrindai, o c yra dviejų lygiagrečių kraštinių ilgis, tada perimetras apskaičiuojamas taip:
Perimetras = a + b + 2c
kur,
- a , b yra trapecijos bazės
- c yra lygi trapecijos pusė
Skirtumas tarp trapecijos ir trapecijos
Apskritai tiek trapecija, tiek trapecija yra vienodi, tačiau skirtumas yra jų kilmės šalyje.
- Trapecija yra britų kilmės, tai keturkampis daugiakampis ir dvimatė figūra, ji turi lygiai vieną porą lygiagrečių kraštinių, priešingų viena kitai. Indijoje mes vadovaujamės britų anglų kalba, todėl vartojamas žodis Trapezium.
- Trapecija yra amerikietiškos kilmės, tai taip pat yra keturkampis daugiakampis, kurio viena pora lygiagrečių vienas kitam priešingų kraštinių. Lygiagrečios kraštinės yra pagrindai, o dar dvi nelygiagrečios kraštinės vadinamos trapecijos kojelėmis.
Trapecijos kampai
Trapecija yra keturkampis, o visų keturkampių kampų suma yra 360 laipsnių. Taigi visų trapecijos vidinių kampų suma yra 360 laipsnių.
Bet kuriai taisyklingai trapecijai, t.y., trapecija, kurios nelygiagrečios kraštinės yra lygios besiribojantiems kampams, suformuotiems tarp lygiagrečios tiesės ir nelygiagrečios tiesės, yra lygi. Taigi šių dviejų kampų suma yra papildoma.
np.tai
Paimkime pavyzdį, patvirtinantį šią lygiašonės trapecijos ABCD sampratą, jei AB lygiagreti CD, o AD yra lygus CD, tada žinome, kad ∠A = ∠B ir ∠C = ∠D tada,
∠A + ∠B + ∠C + ∠D = 360°
Čia ∠A = ∠B ir ∠C = ∠D
∠A + ∠A + ∠C + ∠C = 360°
2 (∠A + ∠C) = 360°
(∠A + ∠C) = 180°
Panašiai (∠B + ∠D) = 180°
Trapecijos įstrižainė
Trapecija yra specialus keturkampio tipas; taigi, trapecija taip pat turi dvi įstrižaines. Skirtingai nuo kai kurių kitų keturkampių, tokių kaip stačiakampiai ar lygiagrečiai, trapecijos įstrižainės neturi vienodo ilgio. Trapecijos įstrižainės neturi vienodo ilgio, o įstrižainių ilgiai priklauso nuo pagrindų ilgių ir trapecijos kampų.
Pavyzdys: Lygiašonės trapecijos ABCD pagrindo kampas ∠A yra 80°, tada suraskite kitą kampą ∠C.
Žinome, kad lygiašonei trapecijai ABCD,
(∠A + ∠C) = 180°
Duota, ∠A = 80°
Dabar 80° + ∠C = 180°
∠C = 180–80
∠C = 100°
Taigi, būtinas kampas ∠C yra 100°
Trapecijos formulės – trapecijos plotas ir perimetras
Su trapecija susijusios formulės apibendrintos šioje lentelėje:
| Nuosavybė | Formulė |
|---|---|
| Plotas | 1/2 × ( a + b ) × h |
| Plotas (lygiašonė trapecija) | 1/2 × [√(c2– (a–b)2) (a+b)] |
| Perimetras | a + b + c + d |
| Perimetras (lygiašonė trapecija) | a + b + 2 c |
| Mediana | (a + b)/2 , |
Žmonės taip pat skaito:
- Rombas
- Trikampis
- Kokia yra trapecijos srities radimo formulė?
Trapecijos pavyzdžiai
1 pavyzdys: Raskite ketvirtąją trapecijos kraštinę, jei kitos trys kraštinės yra 8 cm, 12 cm ir 16 cm, o perimetras yra 40 cm.
Sprendimas:
Perimetras pateikiamas kaip visų jo kraštinių suma. Tegul ilgis o nežinomas yra „x“ vienetai.
Perimetras = 40
40 = 8 + 12 + 16 + x
x = 40 – (8 + 12 + 16)
= 4 cm
Taigi nežinomos kraštinės ilgis yra 4 cm
2 pavyzdys: Trapecijos lygiagrečios kraštinės yra 15 cm ir 11 cm ilgio, o nelygiagrečios – 5 cm ilgio. Apskaičiuokite perimetrą trapecija.
Sprendimas:
Tai lygiašonė trapecija, nes aiškiai paminėta, kad nelygiagrečios 5 cm ilgio kraštinės yra lygios.
Pagal lygiašonį trapeciją, jei dvi nelygiagrečios trapecijos kraštinės yra vienodo ilgio, tada ji vadinama lygiašone trapecija.
Atsižvelgiant į
- a = 15 cm
- b = 11 cm
- c = 5 cm
Perimetras = a + b + 2c
P = 15 + 11 + 2 (5)
P = 15 + 11 + 10
P = 36 cm
3 pavyzdys: Raskite trapecijos, kurios kraštinės yra 12 cm, 14 cm, 16 cm ir 18 cm, perimetrą.
Sprendimas:
P = visų pusių suma
P = 12 + 14 + 16 + 18
P = 60 cm
Vadinasi, trapecijos perimetras yra 60 cm
4 pavyzdys: Raskite trapecijos plotą, kurio lygiagrečių kraštinių suma yra 60 cm, o aukštis 10 cm.
Sprendimas:
Atsižvelgiant į
- Lygiagrečių kraštinių suma 60 cm
- aukštis, h = 10 cm
Trapecijos plotas, A = 1/2 × lygiagrečių kraštinių suma × atstumas tarp lygiagrečių kraštinių
Pakeičiant nurodytas vertybes,
A = 1/2 × 60 × 10
A = 30 × 10
A = 300 cm2
Todėl trapecijos plotas = 300 cm2
Praktikos uždaviniai dėl trapecijos matematikoje
1. Raskite trapecijos, kurios pagrindai 10 cm ir 15 cm, o aukštis 6 cm, plotą.
2. Trapecijos plotas yra 54 kvadratiniai metrai. Jei vienas iš pagrindų yra 12 metrų ilgio, o aukštis 6 metrai, suraskite kito pagrindo ilgį.
3. Apskaičiuokite trapecijos, kurios pagrindai 8 cm ir 14 cm, o nelygiagrečios kraštinės 5 cm ir 7 cm, perimetrą.
4. Nustatykite vidurio segmento ilgį trapecijoje, kur pagrindai yra 18 cm ir 30 cm.
5. Lygiašonės trapecijos kampai prie vieno pagrindo yra 45 laipsnių. Raskite kito pagrindo kampų matmenis. Tarkime, kad trapecija nėra teisinga trapecija.
Santrauka – Trapecija matematikoje
Trapecija yra keturkampis daugiakampis arba keturkampis, kuriam būdinga viena lygiagrečių kraštinių pora, vadinama bazėmis, o kitos dvi kraštinės, žinomos kaip kojos, nėra lygiagrečios. Įprasta kasdieniuose objektuose, pavyzdžiui, lentelėse, trapecija išsiskiria savo geometrinėmis savybėmis: jos aukštis, kuris yra statmenas atstumas tarp pagrindų, ir mediana, jungianti nelygiagrečių kraštų vidurio taškus ir lygiagreti pagrindams.
Trapecijos plotas apskaičiuojamas suvidurkinant pagrindų ilgius ir padauginus iš aukščio, o jos perimetras yra visų jos kraštinių suma. Skirtingos klasifikacijos, tokios kaip skalė, lygiašoniai ir dešinieji trapecijos, kurių kiekviena turi unikalių šoninių ir kampų savybių, trapecijos yra labai svarbios tiek praktikoje, tiek geometrinėje teorijoje.
DUK apie matematikos trapeciją
Kas yra trapecijos forma?
Trapecija yra keturkampis, kuriame tiesių pora visada yra lygiagreti. Jis primena stalo formą. Jo pavadinimas kilęs iš graikų kalbos žodžio trapeze, kuris reiškia stalą.
Kiek trapecijos tipų?
Yra dviejų tipų trapecijos,
- Įprasta trapecija: Kurioje kitos poros tiesių yra lygios.
- Netaisyklinga trapecija: Kurioje kitos poros linijų nėra lygios.
Kiek lygiagrečių kraštinių turi trapecija?
Žinome, kad trapecija yra keturkampis su viena lygiagrečių kraštinių pora. Taigi trapecija turi porą lygiagrečių linijų (kraštinių).
Ar trapeciją galima laikyti keturkampiu?
A turi keturias kraštines, keturias viršūnes ir keturis kampus. Taigi ją galima laikyti keturkampiu, visų keturių vidinių trapecijos kampų suma yra 360 laipsnių.
Ar aikštę galima vadinti trapecija?
Trapecija yra keturkampis, kuriame yra tik viena lygiagrečių kraštinių pora, o kitos dvi kraštinės yra nelygiagrečios. Tačiau kvadrato atveju jis turi dvi lygiagrečių kraštinių poras, todėl jo negalima laikyti trapecija.
Ar trapecijos įstrižainės visada lygios?
Trapecijos įstrižainės gali būti nevienodos. Taisyklingo daugiakampio atveju įstrižainės yra lygios, bet netaisyklingo daugiakampio atveju tai nėra tiesa.
Kokios yra trapecijos savybės?
5 trapecijos savybės yra:
- Trapecijoje pagrindai yra lygiagrečiai vienas kitam.
- Trapecija turi papildomų gretimų kampų.
- Tik viena priešingų kraštinių pora yra lygiagreti.
- Visų trapecijos vidinių kampų suma visada yra 360°.
- Linija, jungianti nelygiagrečių kraštinių vidurio tašką, visada yra lygiagreti pagrindams.
