Vienetinis apskritimas yra apskritimas, kurio spindulys yra 1. Vienetinio apskritimo centras yra ašies pradžioje (0,0). The perimetras Vieneto apskritimo plotas yra 2π vienetai, o vieneto apskritimo plotas yra π vienetai2. Jis turi visas Circle savybes. Vieneto apskritimas turi x lygtį2+ ir2= 1. Šis vienetų ratas padeda apibrėžti įvairias trigonometrines sąvokas.
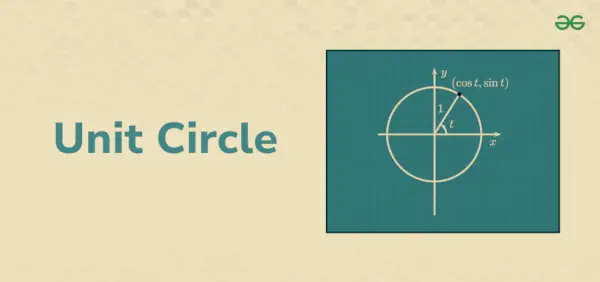
Vieneto ratas
Vieneto ratas dažnai žymimas kaip S1apibendrinimas į aukštesnius matmenis yra vienetinė sfera. Supraskime daugiau apie vieneto ratą, formulę ir išspręstus pavyzdžius.
Kas yra vieneto ratas?
Vienetas Apskritimas yra apskritimas, kurio spindulys yra vienas (1) vienetas. Mes naudojame Dekarto plokštumą, norėdami nubrėžti vienetinį apskritimą, o vienetinis apskritimas yra 2 laipsnių daugianomas su dviem kintamaisiais. Vieneto apskritimas turi įvairių pritaikymų trigonometrijoje ir algebroje ir dažniausiai naudojamas skirtingų trigonometrinių santykių, tokių kaip sin x, cos x, tan x ir kt., reikšmėms rasti.
Vieneto apskritimo apibrėžimas
Matematikoje vienetinį apskritimą apibrėžiame kaip fiksuoto taško, esančio vieno vieneto atstumu nuo apskritimo centro, lokusą. Vienetinio apskritimo spindulys yra vieno vieneto, taigi ir vieneto apskritimo pavadinimas.
Vienetinio apskritimo lygtis
Žinome, kad bet kurio apskritimo, kurio centras (h, k) ir spindulys „r“, lygtis yra
(x – h) 2 + (y – k) 2 = r 2
Vienetinio apskritimo atveju žinome, kad r yra 1 vienetas, taigi vienetinio apskritimo lygtis yra
(x – h) 2 + (y – k) 2 = 1
Vienetinio apskritimo formulė
Jei vienetinio apskritimo centras yra pradžia, ty (h, k) = (0, 0), tada vienetinio apskritimo lygtis yra
x 2 + ir 2 = 1
Vienetinis apskritimas pavaizduotas toliau pateiktame paveikslėlyje, kurio centrinė koordinatė h, k, o kai apskritimas yra pradžioje, h ir k reikšmės yra nulis, o spindulys AP yra lygus 1 vienetui.
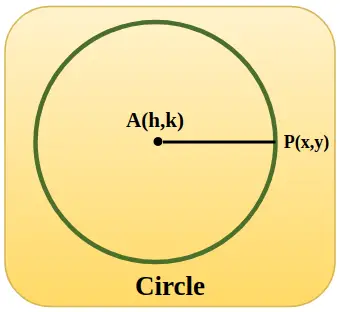
Trigonometrinės funkcijos naudojant vienetų apskritimą
Pitagoro teoremos taikymas vienetiniame apskritime gali būti geriau panaudotas trigonometrinėms funkcijoms suprasti. Tam mes laikome statųjį trikampį, kuris yra vienetinio apskritimo viduje Dekarto koordinačių plokštumoje. Jei pastebėsime, šio apskritimo spindulys žymi stačiakampio trikampio hipotenuzą.
Apskritimo spindulys sudaro vektorių. Dėl to susidaro kampas, tarkime, θ su teigiama x ašimi. Tarkime, kad x yra atitinkamai stačiojo trikampio bazės ilgis, o y yra aukščio ilgis. Be to, spindulio vektoriaus galinių taškų koordinatės yra atitinkamai (x, y).
Stačiakampis trikampis turi atitinkamai kraštines 1, x ir y. Dabar trigonometrinį santykį galima apskaičiuoti taip:
gimp kaip panaikinti pasirinkimą
sin θ = Aukštis/Hipotenuzė = y/1
cos θ = bazė/hipotenūza = x/1
Dabar
- sin θ = y
- cos θ = x
- tan θ = sin θ /cos θ = y/x
Pakeitę θ reikšmes, galime gauti pagrindines visų trigonometrinių funkcijų reikšmes. Panašiai randamos trigonometrinių funkcijų reikšmės skirtingomis reikšmėmis.
Vieneto ratas su Sin Cos ir Tan
Bet kuris vienetinio apskritimo taškas su koordinatėmis (x, y) vaizduojamas naudojant trigonometrines tapatybes kaip, (cosθ, sinθ). Spindulio kampų koordinatės rodo θ reikšmių kosinusą ir sinusą tam tikrai θ reikšmei ir spindulio linijai. Turime cos θ = x, o sin θ = y. Kiekviename kvadrante yra keturios apskritimo dalys, sudarytos 90°, 180°, 270° ir 360° kampu. Spindulio reikšmės yra atitinkamai nuo -1 iki 1. Be to, sin θ ir cos θ reikšmės yra atitinkamai tarp 1 ir -1.
Vieneto apskritimas ir trigonometrinės tapatybės
Kotangento, sekanto ir kosekanto vienetinio apskritimo trigonometrines tapatybes galima apskaičiuoti naudojant sin, cos ir tan tapatybes. Galiausiai gauname stačiakampį trikampį, kurio kraštinės yra atitinkamai 1, x ir y. Apskaičiuojant vieneto apskritimo tapatybes galima išreikšti taip,
- sin θ = y/1
- cos θ = x/1
- tan θ = y/x
- sek θ = 1/x
- cosec θ = 1/m
- vaikiška lovelė θ = x/y
Vieneto apskritimo diagrama
Vienetinė apskritimo diagrama yra diagrama, kurioje yra įvairių kampų trigonometrinės funkcijos sinuso ir kosinuso reikšmės. Žemiau pridedama to paties vieneto apskritimo diagrama,
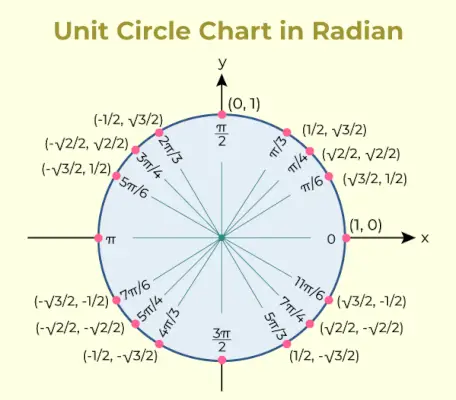
Vienetų apskritimo lentelė
Vienetinio apskritimo lentelėje naudojami trigonometriniai santykiai naudojami vienetinio apskritimo taškų, atitinkančių bendruosius kampus, koordinatėms išvardyti.
| Kampai | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| be | 0 | 1/2 | 1/√ (2) | √3/2 | 1 |
| cos | 1 | √3/2 | 1/√ (2) | 1/2 | 0 |
| taip | 0 | 1/√ (3) | 1 string.valueof java | √(3) | Neapibrėžtas |
| csc | Neapibrėžtas | 2 | √(2) | 23) | 1 |
| sek | 1 | 23) | √(2) | 2 | Neapibrėžtas |
| vaikiška lovelė | Neapibrėžtas | √(3) „Java“ masyvo sąrašo rūšiavimas | 1 | 1/√ (3) | 0 |
Vieneto apskritimo Pitagoro tapatybės
Yra trys Pitagoro tapatybės ir visos jos lengvai įrodomos naudojant vieneto apskritimo koncepciją, kurią sudaro trys Pitagoro tapatybės,
- be2θ + cos2θ = 1
- 1 + taip2θ = sek2i
- 1 + vaikiška lovelė2θ = kosek2i
Vieneto apskritimo kompleksinė plokštuma
Sudėtingi skaičiai ir sudėtinga plokštuma yra lengvai paaiškinami naudojant vienetinio apskritimo sąvoką. Vienetinio apskritimo lygtis sudėtingoje formoje yra
|z| = 1
ARBA
x 2 + ir 2 = 1
Eulerio formoje kompleksinis skaičius vaizduojamas kaip
z = e tai = cos t + i (sin t)
Skaityti daugiau
Išspręsti vieneto apskritimo pavyzdžiai
1 klausimas: įrodykite, kad taškas Q yra vienetiniame apskritime, Q = [1/√(6), √4/√6]
Sprendimas:
Atsižvelgiant į
- Q = [1/√(6), √4/√6]
x = 1/√(6), y = √4/√6
Vieneto apskritimo lygtis yra
x2+ ir2= 1
LHS = (1/√(6))2+ (√4/√6)2
LHS = 1/6 + 4/6 = 5/6 ≠ 1
LHS ≠ RHS
Taigi taškas Q[1/√(6), √4/√6] nėra vienetiniame apskritime.
2 klausimas: apskaičiuokite 30 O naudojant vienetinio apskritimo sin ir cos reikšmes.
Sprendimas:
tan 30° naudojant sin ir cos vertes,
įdegis 30° = (sin 30°)/ (cos 30°)
- be 30° = 1/2
- cos 30° = √(3)/2
įdegis 30° = 1/2/√(3)/2
įdegis 30° = 1/√(3)
3 klausimas: patikrinkite, ar taškas P [1/2, √(3)/2] yra vienetiniame apskritime.
Sprendimas:
Atsižvelgiant į
P = [1/2, √(3)/2]
- x = 1/2
- y = √(3)/2
Vieneto apskritimo lygtis yra
- x2+ ir2= 1
LHS
= (1/2)2+ (√(3)/2)2
= 1/4 + 3/4
= (1 + 3)/4 = 4/4
= 1
= RHS
Praktiniai klausimai apie vienetų ratą
Q1. Patikrinkite, ar taškai A (1/2, 3/2) yra vienetiniame apskritime.
Q2. Patikrinkite, ar taškai A (2, 1/2) yra vienetiniame apskritime.
sesija pasibaigė
Q3. Raskite cos 240° vertę
4 klausimas. Raskite įdegio 320° vertę
Q5. Raskite sin 160° reikšmę
Vieneto ratas – DUK
Kas yra vieneto ratas?
Vienetinis apskritimas apibrėžiamas kaip taško vieta, esanti vienu vienetu atstumu nuo fiksuoto taško. Jo centras yra (0,0), o jo spindulio reikšmė yra 1.
Kaip patikrinti, ar taškas yra ant vieneto apskritimo?
Bet kuris taškas, esantis 2D plokštumoje, kurio forma yra (x, y), įtraukiamas į vienetinę apskritimo lygtį x2+ ir2= 1, kad patikrintumėte, ar jis yra ant apskritimo, ar ne.
Kokia yra vieneto apskritimo formulė?
Vienetinio apskritimo formulė yra formulė, naudojama vienetiniam apskritimui pavaizduoti algebriškai. Vieneto apskritimo formulė pateikiama taip,
x 2 + ir 2 = 1
Kodėl jis vadinamas vieneto ratu?
Vienetinis apskritimas vadinamas vienetiniu apskritimu, nes jo spindulys yra vienas (1) vienetas.
