TRIGONOMETRIJOS LENTELĖ

Trigonometrijos lentelė yra standartinė lentelė, padedanti rasti trigonometrinių santykių reikšmes standartiniams kampams, pvz., 0°, 30°, 45°, 60° ir 90°. Tai susideda iš visų šešių trigonometrinių santykių: sinuso, kosinuso, tangento, kosekanto, sekanto ir kotangento.

Išsamiai sužinokime apie trigonometrijos lentelę.

Turinys

Trigonometrijos lentelė
Trigonometrinių funkcijų lentelė
Trigonometrinių santykių išmokimo triukas
Kaip įsiminti trigonometrinę lentelę
Kaip sukurti trigubo lentelę
Trigonometrinės formulės
Trigonometrinių tapatybių lentelė
Trigonometrinių lentelių pavyzdžiai

Trigonometrinė lentelė yra visų šešių trigonometrinių funkcijų reikšmių išdėstymas jų bendriems kampams lentelės pavidalu.

Trigonometrijos lentelė

Pastaba – Trigonometrija – matematikos šaka, nagrinėjanti stačiakampių trikampių kampų ir kraštinių ryšius.

Trigonometrinių funkcijų lentelė

Trigonometrija turi 6 pagrindines trigonometrines funkcijas, kurios yra sinusas, kosinusas, tangentas, kosekantas, sekantas ir kotangentas. Dabar pažvelkime į trigonometrines funkcijas.

Bet kurio stačiakampio trikampio su statmena (P), baze (B) ir hipotenuse (H) šešios trigonometrinės funkcijos yra tokios:

Trigonometrinių funkcijų lentelė
Funkcija	Apibrėžimas	Atstovavimas	Ryšys su stačiojo trikampio kraštinėmis
Jo	Statmens ir hipotenuzės santykis	be i	Priešinga pusė / hipotenuzė
Kosinusas	Bazės ir hipotenuzės santykis	cos i	Gretima pusė / hipotenuzė
Tangentas	Kampo sinuso ir kosinuso santykis	taip i	Priešinga pusė / gretima pusė
Kosekantas	Nuodėmės θ atvirkštinė vertė	csc i arba cosec i	Hipotenuzė / priešinga pusė
Sekantas	cos θ atvirkštinė vertė	sek i	Hipotenuzė / gretima pusė
Kotangentas	Tan θ atvirkštinė vertė	vaikiška lovelė i	Gretima pusė / priešinga pusė

Pastaba – Trigonometrija yra matematikos šaka, nagrinėjanti trikampių, ypač stačiakampių trikampių, kampų ir kraštinių santykius. Tai apima sinuso, kosinuso, liestinės ir kitų trigonometrinių funkcijų tyrimą ir taikymą įvairių sričių problemoms spręsti.
Pete'o Davidsono pilietybė

Patikrinti : Trigonometrija: formulės, lentelė, tapatybės ir santykiai

Trigonometrinių santykių išmokimo triukas

Išstudijuokite toliau pateiktą lentelę, kad lengvai įsimentumėte trigonometrinius santykius.

Kai kurie žmonės turi garbanotus juodus plaukus, kad sukurtų grožį

sin θ (kai kurie) = statmena (žmonės) / hipotenuzė (turi)

cos θ (garbanoti) = bazė (juoda) / hipotenuzė (plaukai)

tan θ (iki) = statmena (gamyba) / bazė (grožis)

Kaip įsiminti trigonometrinę lentelę

Trigonometrijos lentelę gana lengva prisiminti, jei žinote visas trigonometrijos formules. Taip pat yra triukas, vadinamas vienos rankos triukas įsiminti trigonometrijos lentelę.

Kaip įsiminti trigonometrinę lentelę

1 žingsnis: Aukščiau esančiame paveikslėlyje sinusinės lentelės pirštus suskaičiuokite kairėje pusėje standartiniam kampui.

2 žingsnis: Padalinkite pirštų skaičių kairėje pusėje (apskaičiuokite 1 žingsnyje) iš 4

3 veiksmas: Raskite kvadratinę šaknį iš vertės, apskaičiuotos 2 veiksme.

Patikrinti: Trigonometrijos formulės – visų trigonometrinių tapatybių ir formulių sąrašas

Kaip sukurti trigubo lentelę

Norėdami sukurti standartinių kampų trigonometrinę lentelę, atlikite šiuos veiksmus.

java if else teiginys

1 veiksmas: sukurkite lentelę

Sukurkite lentelę ir išvardinkite visus kampus, pvz 0°, 30°, 45°, 60° ir 90°, viršutinėje eilėje. Pirmame stulpelyje įveskite visas trigonometrines funkcijas sin, cos, tan, cosec, sec ir cot.

2 veiksmas: įvertinkite visų nuodėmės funkcijos kampų vertę.

Norėdami rasti nuodėmės funkcijos reikšmes, padalinkite 0, 1, 2, 3 ir 4 iš 4 ir paimkite kiekvienos reikšmės šaknį atitinkamai kaip

Nes vertė sin 0° = √(0/4) = 0
Panašiai,
sin 30° = √(1/4) = 1/2
sin 45° = √(2/4) = 1/√2
sin 60° = √(3/4) = √3/2
sin 90° = √(4/4) = 1

be 0°	be 30°	be 45°	be 60°	be 90°
0	1/2	1/√2	√3/2	1

3 veiksmas: Įvertinkite visų cos funkcijos kampų reikšmę

Funkcijos cos reikšmė yra priešinga sin funkcijos vertei, ty cos 0° = sin 90°, cos 30° = sin 60° ir cos 45° = sin 45°, taigi

cos 0°	už 30°	cos 45°	cos 60°	cos 90°
1	√3/2	1/√2	1/2	0

4 veiksmas: įvertinkite visų įdegio funkcijos kampų vertę

Tan funkcijos reikšmė lygi sin funkcijai, padalytai iš cos funkcijos, t.y. tan x = sin x / cos x. Visų įdegio funkcijos kampų vertė apskaičiuojama taip:

tan 0° = sin 0° / cos 0° = 0/1 = 0, panašiai

taigi 0°	taigi 30°	taigi 45°	taigi 60°	taigi 90°
0	1/√3	1	√3	Neapibrėžtas

5 veiksmas: įvertinkite visų cosec funkcijos kampų vertę

Funkcijos cosec reikšmė lygi nuodėmės funkcijos atvirkštinei vertei. Cosec 0° reikšmė gaunama imant sin 0° grįžtamąją vertę

cosec 0° = 1 / sin 0° = 1 / 0 = Neapibrėžta. Panašiai,

cosec 0°	cosec 30°	cosec 45°	cosec 60°	cosec 90°
Neapibrėžtas	2	√2	23	1

6 veiksmas: įvertinkite visų sekundės funkcijos kampų vertę

Funkcijos sec reikšmė lygi cos funkcijos atvirkštinei dydžiui. Sec 0° reikšmė gaunama imant cos 0° grįžtamąją vertę

sek. 0° = 1 / cos 0° = 1 / 1 = 1. Panašiai,

sek. 0°	sek 30°	sek. 45°	sek. 60°	sek. 90°
1	23	√2	2	Neapibrėžtas

7 veiksmas: įvertinkite visų lovytės funkcijos kampų vertę

Vaikiškos lovelės funkcijos reikšmė lygi įdegio funkcijos atvirkštinei dydžiui. Vaikiškos lovelės 0° reikšmė gaunama imant įdegio 0° atvirkštinę vertę

vaikiška lovelė 0° = 1 /įdegis 0° = 1 / 0 = neapibrėžta. Panašiai,

lovelė 0°	lova 30°	lova 45°	lova 60°	lova 90°
Neapibrėžtas	√3	1	1/√3	0

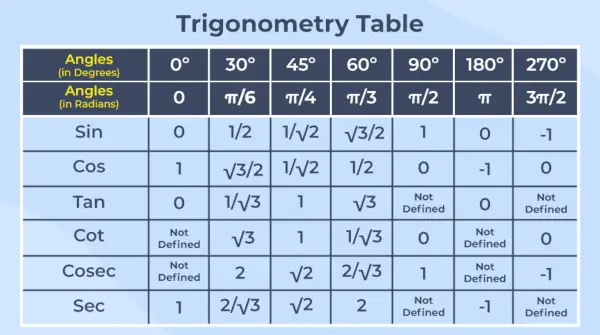
Tokiu būdu galime sukurti tokią trigonometrinių santykių lentelę:

Laipsnių ir radianų trigonometrinė lentelė
Kampas (laipsniais)	Kampas (radianais)	Be	Cos	Taigi	Cosec	Sec	Vaikiška lovelė
0°	0	0	1	0	Neapibrėžtas	1	Neapibrėžtas
30°	p/6	1/2	√3/2	1/√3	2	23	√3
45°	p/4	√2/2	√2/2	1	√2	√2	1
60°	p/3	√3/2	1/2	√3	23	2	1/√3
90°	p/2	1	0	Neapibrėžtas	1	Neapibrėžtas	0

Trigonometrinės formulės

Sužinokime apie kai kurias trigonometrijos formules, susijusias su papildomais ir papildomais kampais.

Papildomi kampai: Kampų pora, kurių suma lygi 90°

Papildomi kampai: Kampų pora, kurių suma lygi 180°

Patikrinti: Trigonometriniai santykiai

Papildomų kampų trigo tapatybės

Papildomų kampų tapatybės pagrįstos dviejų kampų, kurių suma siekia 90 laipsnių (arba π/2 radianų), trigonometrinių funkcijų ryšiu. Tai žinomi kaip bendros funkcijos tapatybės .

Trigonometrinė funkcija	Tapatybė
Jo	sin(90°− i )=cos i
Kosinusas	cos(90°− i )=be i
Tangentas	įdegis (90°− i )=lovytė i
Kotangentas	lovelė (90°− i )=taip i
Sekantas	sek(90°− i )=csc i
Kosekantas	cosec(90°− i )=sek i

Papildomų kampų suaktyvinimo tapatybės

Papildomų kampų tapatybės yra susijusios su dviejų kampų, kurių suma siekia 180 laipsnių (arba π radianų), trigonometrinėmis funkcijomis.

Trigonometrinė funkcija	Tapatybė
Jo	sin(180°− i )=be i
Kosinusas	cos(180°− i )=−cos i
Tangentas	įdegis (180°− i )=−deg i
Kotangentas	lovelė (180°− i )=−lovytė i
Sekantas	sek(180°− i )=−sek i
Kosekantas	cosec(180°− i )=cosec i

Trigonometrinių tapatybių lentelė

Trigonometrinės tapatybės yra tapatybės, kurios labai naudojamos sprendžiant trigonometrines problemas. Yra įvairių trigonometrinių tapatybių, tačiau trys pagrindinės trigonometrinės tapatybės yra:

Trigonometrinių tapatybių lentelė
Trigonometrinis tapatumas	Formulė
Pitagoro tapatybė	be²θ + cos²θ = 1
Sekanto-tangento tapatybė	sek²θ – taip²θ = 1
Kosekanto-kotangento tapatybė	cosec²θ – vaikiška lovelė²θ = 1

Taip pat patikrinkite:

Trigonometriniai santykiai

Atvirkštinės trigonometrinės tapatybės

Aukštis ir atstumai

Trigonometrinių lentelių pavyzdžiai

Išspręskime keletą trigonometrinės lentelės klausimų.

1 pavyzdys: Jei sin θ = 4/5, tada raskite visas trigonometrines reikšmes.

Pašalinkite pirmąjį simbolį „Excel“.

Sprendimas:

Štai mes turime,

sin θ = 4/5

kaip, sin θ = statmena / hipotenūza

taigi mes turime statmeną (P) = 4 ir hipotenuzą (H) = 5

Taigi pagal Pitagoro teoremą H ² = P ² +B ²

Sužinokime bazės (B) reikšmę

5²= B²+ 4²
25 = B²+ 16
25–16 = B²
B²= 9
B = 3

Dabar mes turime,
Bourne-gain apvalkalas

Sin θ = statmena/hipotenuzė
= AB/AC = 4/5

Kosinusas θ = bazė/hipotenuzė
= BC/AC = 3/5

Liestinė θ = statmena / bazė
= AB/BC = 4/3

Kosekantas θ = hipotenuzė / statmena
= AC/AB = 5/4

Sekantas θ = hipotenuzė / bazė
= AC/BC = 5/3

Kotangentė θ = bazė / statmena
= BC/AB = 3/4

2 pavyzdys: Raskite cos 45° + 2 sin 60° – tan 60° reikšmę.

Sprendimas:

Iš trigonometrijos lentelės

cos 45° = 1/√2, sin 60° = √3/2 ir tan 60° = √3

Taigi,

cos 45° + 2 sin 60° – tan 60° = 1/√2 + 2(√3/2) – √3
= 1/√2

3 pavyzdys: Raskite cos 75° reikšmę.

Sprendimas:

Mes tai žinome,

cos 75° = cos (45° + 30°) {as, cos (A + B) = cos A cos B – sin A sin B}
= cos 45° cos 30° – sin 45° sin 30°
= 1/√2 × √3/2 – 1/√2 × 1/2
= (√3 – 1)/2√2

cos 75°= (√3 – 1)/2√2.
hrithik roshan

Išvada – trigonometrijos lentelė

Trigonometrijos lentelė pateikia išsamią trigonometrinių funkcijų sinuso, kosinuso, liestinės, kosekanto, sekanto ir kotangento nuorodą kartu su atitinkamomis įvairių kampų reikšmėmis. aš t tarnauja kaip vertingas sprendimo įrankis trigonometrines lygtis, analizuoti geometrinius ryšius ir suprasti periodinių reiškinių elgesį. Ar viduje matematikos, fizikos, inžinerijos ar kitose srityse, trigonometrijos lentelė padeda atlikti skaičiavimus, spręsti problemas ir vizualizuoti, padeda giliau suprasti trigonometrines sąvokas ir jų taikymą realaus pasaulio scenarijuose.