į Kosinuso funkcija arba cos Trumpai tariant, funkcija yra viena iš šešių Trigonometrinės funkcijos trigonometrijos pagrindas. Trigonometrijoje kosinusas pateikiamas kaip stačiakampio trikampio pagrindo ir hipotenuzės santykis. Kosinuso funkcija pavaizduota kaip Cos x, kur x yra kampas, kuriam apskaičiuojamas kosinuso santykis. Kalbant apie funkciją, galime pasakyti, kad x yra kosinuso funkcijos įvestis arba sritis.

Jis plačiai naudojamas įvairiuose dalykuose, tokiuose kaip fizika, geometrija ir inžinerija, be kita ko, paprastai panaudojant periodiškumą. Pavyzdžiui, jis naudojamas garso bangų banginiam pobūdžiui apibrėžti, elektros srauto per plokščią paviršių skaičiavimams ir kt. Šiame straipsnyje mes išsamiai sužinome, kas yra kosinuso funkcija, domenas ir diapazonas kosinuso funkcijos, periodo ir kosinuso funkcijos grafiko.

Turinys

• Kas yra kosinuso funkcija?
• Cos vieneto rate
• Kosinuso funkcijos grafikas
• Atvirkštinė kosinuso funkcija
• Kosinuso funkcija skaičiavime
• Cos funkcijų tapatybės

Kas yra kosinuso funkcija?

Kosinuso funkcija yra trigonometrinė funkcija, kuri iš esmės yra periodinė. Kosinuso funkcija išreiškiama kaip cos x, kur x yra vienas iš stačiakampio trikampio smailiųjų kampų. Kosinuso funkcija nustato bazės ir hipotenuzės santykį, esant tam tikrai x reikšmei. Kosinuso funkcija sutrumpinta kaip cos(x) arba cos(θ), kur x yra kampas radianais, o teta θ yra kampas laipsnių apskritai. Kosinuso funkciją galima apibrėžti naudojant vienetinį apskritimą, ty vieneto spindulio apskritimą, kaip matysime vėliau šiame straipsnyje. Jis yra periodinio pobūdžio ir kartoja savo reikšmes po kiekvieno kampų pasukimo. Dekarto plokštumoje jis gali būti vadinamas hipotenuzės vektoriniu komponentu, lygiagrečiu x ašiai.

Kosinuso funkcijos apibrėžimas

Kosinuso funkcija apibrėžiama stačiakampiame trikampyje kaip kraštinės, esančios greta atitinkamo kampo, ilgio ir hipotenuzės ilgio santykis. Matematiškai kosinuso funkcija pateikiama kaip

Cos x = Cos θ = pagrindo ilgis / hipotenuzos ilgis = b/h = OB/OA

kur x yra kampas radianais, o θ yra lygiavertis kampas laipsniais.

Cos funkcijos domenas ir diapazonas

Žinome, kad funkcijai domenas yra leistinos įvesties reikšmės, o diapazonas yra tos konkrečios įvesties ar domeno vertės išvesties vertė. Taigi galime daryti prielaidą, kad funkcija veikia kaip procesorius, kuris priima įvestį, apdoroja jį ir suteikia tam tikrą išvestį. Cos funkcijos domenas ir diapazonas aptariami toliau:

• Kosinuso funkcijos sritis: R y., visų realiųjų skaičių aibė.
• Kosinuso funkcijos diapazonas: [-1, 1], t. y. išvestis kinta tarp visų realiųjų skaičių nuo -1 iki 1.

Kosinuso funkcijos laikotarpis

The funkcija yra periodinio pobūdžio, t.y. kartojasi po 2π arba 360°. Kitaip tariant, tai kartojasi po kiekvieno pilno apsisukimo. Vadinasi, kosinuso funkcijos periodas yra pilnas sukimasis arba kampas 360° (arba 2π).

Kosinuso funkcijos atvirkštinė vertė

Kosinuso funkcijos grįžtamasis dydis yra žinomas kaip sekantas funkcija arba sek trumpiau tariant. Matematiškai kosinuso funkcijos atvirkštinė vertė pateikiama kaip

tat pilna forma

sek(θ) = 1/cos(θ)

Pagal taisykles Abipusiai , jei Cos x padauginsime iš Sec x, sandauga visada bus 1.

Kosinuso funkcijos grafikas

Kosinuso funkcijos grafikas panašus į sinuso funkcijos grafiką su esminiu skirtumu, kad esant x = 0 sin funkcijos grafikas eina nuo pradžios, o esant x = 0, kosinuso funkcijos grafikas eina iš (0, 1) ties y ašimis. Toliau pateikiamas kosinuso funkcijos reikšmės grafikas, ty y = cos x

Aukščiau aptartos savybės gali būti matomos grafike kaip funkcijos periodiškumas.

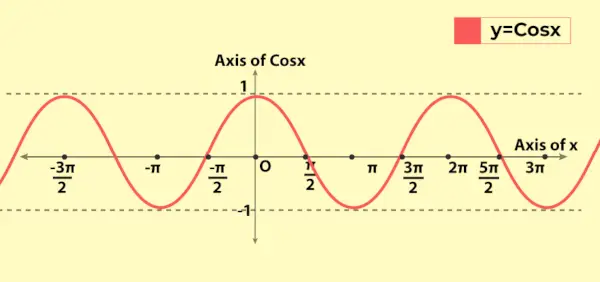
Kosinuso funkcijos kitimas grafike

Kadangi kosinuso funkcijos diapazonas yra [-1, 1], todėl grafike jis kinta nuo -1 iki 1. Jis parodo savo periodiškumą, nes grafikas kartojasi po kiekvieno ilgio 2π x ašyje. Tai rodo, kad kosinuso funkcijos periodas yra 2π (arba 360°).

Cos vieneto rate

Kosinuso funkciją galima apibrėžti naudojant vienetinį apskritimą. Supraskime, kaip galime apibrėžti kosinuso funkciją vieneto apskritimo atžvilgiu.

Apsvarstykite tiesės atkarpą OA, besisukančią apie tašką O, kur O yra stačiakampės plokštumos pradžia. Taigi, OA sukimasis apibūdina vienetinį apskritimą (vienetinio spindulio apskritimą), kurio centras yra O pradžioje, o taškas A visada yra ant šio apskritimo. Jei nuleisime statmeną nuo A ant x ašies ir susikirtimo tašką vadiname B, o θ yra kampas, kurį OA sudaro teigiama x ašies kryptimi, tada cos(θ) = hipotenuzės projekcija x -ašys = OB/|OA| = OB (nes |OA| = 1 vienetas).

Atkreipkite dėmesį, kad kryptis OB yra svarbi, kaip matyti toliau pateiktuose paveikslėliuose. Žalias segmentas žymi ilgį / dydį, o rodyklė nurodo cos(θ) kryptį (+ve arba -ve).

Atkreipkite dėmesį, kad cos (θ) reikšmė yra teigiama θ, priklausančiai pirmajam ir ketvirtajam kvadrantui, o neigiama θ, priklausančiam antrajam ir trečiajam kvadrantui.

Atvirkštinė kosinuso funkcija

Atvirkštinė kosinuso funkcija, žinoma kaip lanko-kosinusas funkcija ir sutrumpinta kaip arccos (x) arba cos ^-1 (x) apibrėžiamas taip

cos(x) = y

⇒ cos ^-1 (y) = x

Atvirkštinės kosinuso funkcijos sritis ir diapazonas

Atvirkštinės kosinuso funkcijos domenas ir diapazonas yra paminėti toliau:

• Atvirkštinės kosinuso funkcijos sritis: Visi realieji skaičiai diapazone [-1, 1]
• Atvirkštinės kosinuso funkcijos diapazonas: Visi realieji skaičiai diapazone [0, π]

Hiperbolinio kosinuso funkcija

Hiperbolinės funkcijos yra analoginės trigonometrinės funkcijos atitikmenys, kurių algebrinė išraiška yra eksponentinės funkcijos terminais. Hiperbolinio kosinuso funkcija sutrumpinta kaip cosh (x) kur x yra hiperbolinis kampas yra hiperbolinės geometrijos sąvoka. Panašiai kaip (cos(x), sin(x)) reiškia tašką vienetiniame apskritime, (cosh(x), sinh(x)) reiškia tašką vienetinėje hiperbolėje, ty xy = 1, kur sinh(x) reiškia hiperbolę sinuso funkcija. Hiperbolinės cos funkcijos algebrinė plėtra pateikta kaip

cosh(x) = (e ^x + ir ^-x )/2

Išsamesnė informacija apie hiperbolines funkcijas nepatenka į šio straipsnio taikymo sritį, tačiau galite pasiskaityti Šis straipsnis .

Kosinuso funkcija skaičiavime

Matematikos skaičiavimo šaka nagrinėja diferenciacija ir integracija tam tikros funkcijos. Funkcijos diferencijavimas yra funkcijos pokyčio greitis nepriklausomo kintamojo atžvilgiu, o integracija yra atvirkštinis diferenciacijos procesas, kurio tikslas yra rasti funkcijos, kurios išvestinė yra, integralą.

Kosinuso funkcijos išvestinė

The išvestinė kosinuso funkcija yra lygi sinuso funkcijos neigiamai. Matematiškai

d(cos(x))/dx = -sin(x)

Kosinuso funkcijos integravimas

The neapibrėžtas integralas kosinuso funkcija yra lygi sinuso funkcijai. matematiškai –

∫cos(x)dx = sin(x) + C, kur C yra integravimo konstanta.

Sinuso ir kosinuso funkcijos

Šioje diagramoje parodytas pagrindinis skirtumas tarp sinuso ir kosinuso funkcijų:

Skirtumas tarp sinuso ir kosinuso funkcijų

Šioje lentelėje pateikiami skirtumai tarp sinuso ir kosinuso funkcijų –

Cos verčių lentelė

Toliau pateiktoje lentelėje pateiktos kosinuso funkcijos reikšmės kai kuriems bendriems kampams pirmajame Dekarto plokštumos kvadrante –

Naudodami šias reikšmes galime lengvai apskaičiuoti kitų įprastų kampų, pvz., 15°, 75°, 195°, -15° ir tt, vertes, naudodamiesi formulėmis cos (x + y) ir cos (x – y), aprašytas vėliau. straipsnis.

Patikrinti, Trigonometrinė lentelė

Cos funkcijų tapatybės

Žemiau paminėtos pagrindinės trigonometrinės tapatybės, susijusios su kosinuso funkcija:

• be²(x) + cos²(x) = 1
• cos(x + y) = cos(x)cos(y) – sin(x)sin(y)
• cos(x – y) = cos(x)cos(y) + sin(x)sin(y)
• cos(-x) = cos(x)
• cos(x) = 1/sek(x)
• cos 2x = cos²x – nuodėmė²x = 1 – 2sin²x = 2cos²x – 1 = (1 – įdegis²x/1 + įdegis²x)
• cos 3x = 4cos³x – 3cos x

susiję straipsniai

• Trigonometrinių funkcijų diferenciacija
• Atvirkštinės trigonometrinės funkcijos
• Atvirkštinės trigubos išvestinės priemonės

Išspręsti kosinuso funkcijos pavyzdžiai

Štai keletas išspręstų pavyzdžių, padėsiančių geriau suprasti kosinuso funkcijos sąvoką.

1 pavyzdys: Kokios yra didžiausios ir minimalios kosinuso funkcijos reikšmės?

Sprendimas:

Maksimali kosinuso funkcijos reikšmė yra 1, kai kampas yra 0° ir 180°, o mažiausia funkcijos reikšmė yra -1, kai kampas 180°.

2 pavyzdys. Kokiu kampu (-iais) diapazone [0, 360] yra kosinuso funkcijos reikšmė 0?

Sprendimas:

Kosinuso funkcijos reikšmė 0 kampuose 90° ir 270°.

3 pavyzdys: Kuriems kvadrantams kosinuso funkcijos reikšmė yra neigiama?

Sprendimas:

Kosinuso funkcija yra neigiama II^ndir III^rdkvadrantai.

4 pavyzdys: Apskaičiuokite cos reikšmę (45°).

Sprendimas:

gauti masyvo ilgį c

Pagal anksčiau pateiktą 4 tapatybę cos(-x) = cos(x).

Todėl cos(-45°) = cos(45°) = 1/√2

5 pavyzdys: Apskaičiuokite cos(15°) reikšmę.

Sprendimas:

Naudojant aukščiau pateiktą 3 tapatybę –

cos(15degree) = cos(45degree – 30degree) ewline = cos(45degree)cos(30degree) + sin(45degree)sin(45degree) ewline = frac{1}{sqrt2} imesfrac{sqrt3}{2} + frac{1}{sqrt2} imes frac{1}{2} ewline = frac{sqrt3 + 1}{2sqrt2}

6 pavyzdys: kas yra cos ^-1 (1/2) diapazone [0,π]?

Sprendimas:

Tegul cos^-1(1/2) = y.

Todėl cos(y) = 1/2 ⇒ y = π/3 aukščiau pateiktame diapazone.

Taigi atsakymas yra π/3.

7 pavyzdys: kokia yra cos(-15°) reikšmė?

Sprendimas:

Naudojant anksčiau pateiktą 3 tapatybę –

cos(-15degree) ewline = cos(30degree – 45degree) ewline = cos(30degree)cos(45degree) + sin(30degree)sin(45degree) ewline = frac{sqrt3}{2} imesfrac{1}{sqrt{2}} + frac{1}{2} imesfrac{1}{sqrt2} ewline = frac{sqrt3 + 1}{2sqrt2} .

Arba taip pat galime naudoti tapatybę cos(-x) = cos(x) ir naudoti cos(15°) reikšmę, apskaičiuotą 5 pavyzdyje.

8 pavyzdys: Apskaičiuokite plotą po kosinuso funkcijos grafiku nuo x = 0 iki x = π/2.

Sprendimas:

Duotą plotą galima apskaičiuoti sprendžiant šį apibrėžtąjį integralą –

int_0^{frac{pi}{2}}cos(x)dx ewline = sin(frac{pi}{2}) – sin(0) ewline = 1 – 0 ewline = 1

Todėl atsakymas yra 1 kvadrato vienetas.

9 pavyzdys: jei cos(x) = π/3, raskite cos(3x) reikšmę (dešimtaine forma, dviejų skaitmenų po kablelio tikslumu).

Sprendimas:

Naudojant tapatybę – cos(3x) = 4cos³(x) – 3cos (x) –

cos(3x) = 4⨉(π/3)³-3⨉(π/3) ≅ 4,59 – π = 1,45

10 pavyzdys: Raskite cos(120°) reikšmę.

Sprendimas:

Cos tapatybės naudojimas (2x)

cos(120°) = cos(2⨉60°) = 1 – 2 sin²(60°) = 1–2⨉ (√3/2)²= 1 – 3/2 = -1/2

Praktiniai klausimai: Cos funkcijos

Q1. Kokia formulė apskaičiuojama stačiakampio trikampio kampo cos?

Q2. Kokia yra geometrinė cos interpretacija Dekarto plokštumoje?

Q3. Apskaičiuokite cos(120°) reikšmę.

4 klausimas. Raskite cos vertę ^-1 (√3/2) diapazone [π, 2π].

Q5. Jei stulpas meta ant žemės tokio pat ilgio šešėlį, suraskite saulės kampą žemės atžvilgiu, jei saulė yra rytų kryptimi.

Santrauka – kosinuso funkcija

Kosinuso funkcija, žymima kaip cos(x), yra pagrindinė trigonometrinė funkcija, apibrėžiama kaip stačiakampio trikampio pagrindo ir hipotenuzos santykis ir dėl savo periodiškumo būtina įvairiose srityse, pvz., fizikos, inžinerijos ir geometrijos. , kuris yra svarbus modeliuojant bangų elgesį. Jis turi visų realiųjų skaičių domeną ir diapazoną nuo -1 iki 1, kartodamas savo ciklą kas 2 Pi radianų arba 360 laipsnių kampu, matyti iš jo bangos grafiko, kuris prasideda nuo (0,1). Kalbant apie skaičiavimą, cos(x) išvestinė yra − sin( x ), o jo integralas duoda sin( x )+ C , su C kaip integracijos konstanta. Ši funkcija taip pat taikoma hiperbolinėms formoms, tokioms kaip cosh (x), pagerinant jos taikymą įvairiuose matematiniuose kontekstuose ir sprendimuose, įskaitant bangų skaičiavimus ir virpesius fizinėse sistemose.

Kosinuso funkcija: DUK

1. Kas yra kosinuso funkcija?

Kosinuso funkcija yra viena iš pagrindinių trigonometrinių funkcijų. Jis apibrėžiamas stačiakampiame trikampyje kaip kraštinės, esančios greta atitinkamo kampo, ilgio ir hipotenuzės ilgio santykis.

2. Ar trigonometrijoje Cos ir Cosinus yra vienodi?

Taip. cos yra kosinuso funkcijos santrumpa / trumpoji forma.

3. Kas yra Cos funkcijos diapazonas?

Cos arba kosinuso funkcijos diapazonas yra visi realieji skaičiai nuo -1 iki 1, ty [-1,1].

4. Kas yra Cos funkcijos domenas?

Cos arba kosinuso funkcijos sritis yra visų realiųjų skaičių ser, ty R .

5. Kokia yra didžiausia kosinuso funkcijos reikšmė?

Didžiausia kosinuso funkcijos reikšmė yra 1, kai visi kampai atitinka 0° arba 360°.

6. Kokia yra minimali kosinuso funkcijos reikšmė?

Mažiausia kosinuso funkcijos reikšmė yra -1 visiems kampams, atitinkantiems 180°.

7. Kaip rasti Cos(-x) reikšmę?

Cos(-x) reikšmę galima apskaičiuoti apskaičiuojant cos(x) reikšmę, nes egzistuoja tokia tapatybė: cos(-x) = cos(x).

8. Kaip pavaizduoti kosinuso funkciją?

Norėdami nubrėžti kosinuso funkcijos grafiką Dekarto plokštumoje, žr., kad x ašis reiškia kampus radianais (arba laipsniais), o y ašį - kaip kosinuso funkcijos reikšmes atitinkamam kampui x ašyje. Dabar

• 1 žingsnis: Paimkite x ašies poaibį, kuriam norite nubraižyti grafiką.
• 2 žingsnis: Padalinkite x ašį šiame diapazone į vienodo atstumo taškus (t. y. tarp visų potaškių yra vienoda erdvė). Atkreipkite dėmesį, kuo didesnis padalijimų skaičius, tuo didesnis gaunamo grafiko tikslumas.
• 3 veiksmas: Kiekviename iš šių popunktių x pažymėkite tašką (x, cos (x)) grafike.
• 4 veiksmas: Sujunkite visus pažymėtus taškus, kad gautumėte kosinuso funkcijos grafiką (jūsų pasirinktam x ašies poaibiui).

9. Kaip rasti kosinuso funkcijos periodą?

Kosinuso funkcijos laikotarpis reiškia minimalų reikšmių diapazoną, po kurio funkcija pradeda kartotis. Žinome, kad kosinuso funkcija kartojasi po kiekvieno pilno sukimosi, o tai reiškia 2π radianus. Todėl kosinuso funkcijos periodas yra 2π radianai arba 360°.

10. Kas yra kosinuso funkcijos amplitudė?

Kosinuso funkcijos amplitudė reiškia maksimalų funkcijos vertės poslinkį nuo vidutinės padėties, ty x ašies. Kosinuso funkcijos amplitudė yra 1, nes didžiausias poslinkis yra 1 (vertėms -1 ir 1 atitinkamai 180 ir 0 laipsnių kampu. Atkreipkite dėmesį, kad kosinuso funkcijos diapazonas yra [-amplitudė, amplitudė].