Ši pamoka yra pradedantiesiems skirtas vadovas mokymosi duomenų struktūros ir algoritmai naudojant Python. Šiame straipsnyje aptarsime integruotas duomenų struktūras, pvz., sąrašus, eilutes, žodynus ir kt., ir kai kurias vartotojo nustatytas duomenų struktūras, pvz. susietus sąrašus , medžiai , grafikus ir tt, o taip pat paieškos ir rūšiavimo algoritmai, naudojant gerus ir gerai paaiškintus pavyzdžius bei praktinius klausimus.

Sąrašai

Python sąrašai yra sutvarkyti duomenų rinkiniai, kaip ir masyvai kitomis programavimo kalbomis. Sąraše leidžiami įvairių tipų elementai. Python List įgyvendinimas yra panašus į Vectors C++ arba ArrayList JAVA. Brangi operacija yra elemento įterpimas arba ištrynimas iš sąrašo pradžios, nes visus elementus reikia perkelti. Įterpimas ir ištrynimas sąrašo pabaigoje taip pat gali kainuoti, jei iš anksto paskirta atmintis užsipildo.

Pavyzdys: Python sąrašo kūrimas

List = [1, 2, 3, 'GFG', 2.3] print(List)>

[1, 2, 3, 'GFG', 2.3]>

Sąrašo elementus galima pasiekti naudojant priskirtą indeksą. Python sąrašo pradžios indekse seka yra 0, o pabaigos indeksas (jei yra N elementų) N-1.

Pavyzdys: Python sąrašo operacijos

# Creating a List with # the use of multiple values List = ['Geeks', 'For', 'Geeks'] print('
List containing multiple values: ') print(List) # Creating a Multi-Dimensional List # (By Nesting a list inside a List) List2 = [['Geeks', 'For'], ['Geeks']] print('
Multi-Dimensional List: ') print(List2) # accessing a element from the # list using index number print('Accessing element from the list') print(List[0]) print(List[2]) # accessing a element using # negative indexing print('Accessing element using negative indexing') # print the last element of list print(List[-1]) # print the third last element of list print(List[-3])>

List containing multiple values: ['Geeks', 'For', 'Geeks'] Multi-Dimensional List: [['Geeks', 'For'], ['Geeks']] Accessing element from the list Geeks Geeks Accessing element using negative indexing Geeks Geeks>

Tuple

Python eilės yra panašūs į sąrašus, bet tuples yra nekintamas gamtoje, t. y. vieną kartą sukūrus, jo keisti negalima. Kaip ir sąraše, sekcijoje taip pat gali būti įvairių tipų elementų.

„Python“ programoje eilutės sukuriamos pateikiant reikšmių seką, atskirtą „kableliais“, naudojant skliaustus duomenų sekos grupavimui arba be jų.

Pastaba: Norint sukurti vieno elemento eilutę, turi būti kablelis. Pavyzdžiui, (8,) sukurs seką, kurios elementas yra 8.

Pavyzdys: Python Tuple operacijos

# Creating a Tuple with # the use of Strings Tuple = ('Geeks', 'For') print('
Tuple with the use of String: ') print(Tuple) # Creating a Tuple with # the use of list list1 = [1, 2, 4, 5, 6] print('
Tuple using List: ') Tuple = tuple(list1) # Accessing element using indexing print('First element of tuple') print(Tuple[0]) # Accessing element from last # negative indexing print('
Last element of tuple') print(Tuple[-1]) print('
Third last element of tuple') print(Tuple[-3])>

Tuple with the use of String: ('Geeks', 'For') Tuple using List: First element of tuple 1 Last element of tuple 6 Third last element of tuple 4>

Nustatyti

Python rinkinys yra kintamas duomenų rinkinys, neleidžiantis dubliuotis. Rinkiniai iš esmės naudojami narystės testavimui ir pasikartojančių įrašų pašalinimui. Čia naudojama duomenų struktūra yra maišos apdorojimas, populiarus metodas, skirtas vidutiniškai įterpti, ištrinti ir pereiti O(1).

Jei toje pačioje indekso pozicijoje yra kelios reikšmės, tada vertė pridedama prie tos indekso pozicijos, kad būtų sudarytas susietasis sąrašas. „CPython Sets“ yra įdiegtas naudojant žodyną su netikrais kintamaisiais, kur pagrindiniai elementai nustatomi labiau optimizuodami laiko sudėtingumą.

Nustatyti įgyvendinimą:

Rinkiniai su daugybe operacijų vienoje maišos lentelėje:

Pavyzdys: Python rinkinio operacijos

# Creating a Set with # a mixed type of values # (Having numbers and strings) Set = set([1, 2, 'Geeks', 4, 'For', 6, 'Geeks']) print('
Set with the use of Mixed Values') print(Set) # Accessing element using # for loop print('
Elements of set: ') for i in Set: print(i, end =' ') print() # Checking the element # using in keyword print('Geeks' in Set)>

Set with the use of Mixed Values {1, 2, 4, 6, 'For', 'Geeks'} Elements of set: 1 2 4 6 For Geeks True>

Užšaldyti rinkiniai

Užšaldyti rinkiniai Python yra nekintantys objektai, kurie palaiko tik metodus ir operatorius, kurie sukuria rezultatą nepaveikdami fiksuoto rinkinio ar rinkinių, kuriems jie taikomi. Nors rinkinio elementus galima bet kada keisti, fiksuoto rinkinio elementai po sukūrimo išlieka tokie patys.

Pavyzdys: Python Frozen rinkinys

# Same as {'a', 'b','c'} normal_set = set(['a', 'b','c']) print('Normal Set') print(normal_set) # A frozen set frozen_set = frozenset(['e', 'f', 'g']) print('
Frozen Set') print(frozen_set) # Uncommenting below line would cause error as # we are trying to add element to a frozen set # frozen_set.add('h')>

Normal Set {'a', 'b', 'c'} Frozen Set frozenset({'f', 'g', 'e'})>

Styga

Python stygos yra nekintantis baitų masyvas, vaizduojantis Unikodo simbolius. Python neturi simbolių duomenų tipo, vienas simbolis yra tiesiog eilutė, kurios ilgis yra 1.

Pastaba: Kadangi eilutės yra nekintamos, pakeitus eilutę bus sukurta nauja kopija.

Pavyzdys: Python stygų operacijos

String = 'Welcome to GeeksForGeeks' print('Creating String: ') print(String) # Printing First character print('
First character of String is: ') print(String[0]) # Printing Last character print('
Last character of String is: ') print(String[-1])>

Creating String: Welcome to GeeksForGeeks First character of String is: W Last character of String is: s>

Žodynas

Python žodynas yra netvarkingas duomenų rinkinys, kuriame saugomi duomenys raktų:reikšmių poros formatu. Tai kaip maišos lentelės bet kuria kita kalba, kurios laiko sudėtingumas yra O(1). Python žodyno indeksavimas atliekamas raktų pagalba. Jie yra bet kokio tipo maišos, t. y. objektai, kurie niekada negali keistis, pvz., eilutės, skaičiai, eilės ir tt Galime sukurti žodyną naudodami riestinius skliaustus ({}) arba žodyno supratimą.

Pavyzdys: Python žodyno operacijos

# Creating a Dictionary Dict = {'Name': 'Geeks', 1: [1, 2, 3, 4]} print('Creating Dictionary: ') print(Dict) # accessing a element using key print('Accessing a element using key:') print(Dict['Name']) # accessing a element using get() # method print('Accessing a element using get:') print(Dict.get(1)) # creation using Dictionary comprehension myDict = {x: x**2 for x in [1,2,3,4,5]} print(myDict)>

Creating Dictionary: {'Name': 'Geeks', 1: [1, 2, 3, 4]} Accessing a element using key: Geeks Accessing a element using get: [1, 2, 3, 4] {1: 1, 2: 4, 3: 9, 4: 16, 5: 25}>

Matrica

Matrica yra 2D masyvas, kuriame kiekvienas elementas yra griežtai tokio paties dydžio. Norėdami sukurti matricą, naudosime NumPy paketas .

Pavyzdys: Python NumPy matricos operacijos

import numpy as np a = np.array([[1,2,3,4],[4,55,1,2], [8,3,20,19],[11,2,22,21]]) m = np.reshape(a,(4, 4)) print(m) # Accessing element print('
Accessing Elements') print(a[1]) print(a[2][0]) # Adding Element m = np.append(m,[[1, 15,13,11]],0) print('
Adding Element') print(m) # Deleting Element m = np.delete(m,[1],0) print('
Deleting Element') print(m)>

Išvestis

[[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]] Accessing Elements [ 4 55 1 2] 8 Adding Element [[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] Deleting Element [[ 1 2 3 4]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]]>

Bytearray

Python Bytearray suteikia kintamą sveikųjų skaičių seką diapazone 0 <= x < 256.

Pavyzdys: Python Bytearray operacijos

# Creating bytearray a = bytearray((12, 8, 25, 2)) print('Creating Bytearray:') print(a) # accessing elements print('
Accessing Elements:', a[1]) # modifying elements a[1] = 3 print('
After Modifying:') print(a) # Appending elements a.append(30) print('
After Adding Elements:') print(a)>

Creating Bytearray: bytearray(b'x0cx08x19x02') Accessing Elements: 8 After Modifying: bytearray(b'x0cx03x19x02') After Adding Elements: bytearray(b'x0cx03x19x02x1e')>

Susietas sąrašas

A susietas sąrašas yra linijinė duomenų struktūra, kurios elementai nėra saugomi gretimose atminties vietose. Elementai susietame sąraše yra susieti naudojant nuorodas, kaip parodyta toliau pateiktame paveikslėlyje:

Susietą sąrašą rodo žymeklis į pirmąjį susieto sąrašo mazgą. Pirmasis mazgas vadinamas galva. Jei susietas sąrašas tuščias, tada antraštės reikšmė yra NULL. Kiekvienas sąrašo mazgas susideda iš mažiausiai dviejų dalių:

• Duomenys
• Rodyklė (arba nuoroda) į kitą mazgą

Pavyzdys: susieto sąrašo apibrėžimas Python

# Node class class Node: # Function to initialize the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize # next as null # Linked List class class LinkedList: # Function to initialize the Linked # List object def __init__(self): self.head = None>

Sukurkime paprastą susietą sąrašą su 3 mazgais.

# A simple Python program to introduce a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3)  '''  Three nodes have been created.  We have references to these three blocks as head,  second and third  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | None | | 2 | None | | 3 | None |  +----+------+ +----+------+ +----+------+  ''' llist.head.next = second; # Link first node with second  '''  Now next of first Node refers to second. So they  both are linked.  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | o-------->| 2 | null | | 3 | null |  +----+------+ +----+------+ +----+------+ ''' antras.kitas = trečias ; # Susiekite antrąjį mazgą su trečiuoju mazgu ''' Dabar kitas antrojo mazgas reiškia trečiąjį. Taigi visi trys mazgai yra susieti.  liste.galva antras trečdalis | | |  | | |  +----+------+ +----+------+ +----+------+ | 1 | o-------->| 2 | o-------->| 3 | null |  +----+------+ +----+------+ +----+------+ '''>

Susieto sąrašo peržiūra

Ankstesnėje programoje sukūrėme paprastą susietą sąrašą su trimis mazgais. Pereikime sukurtą sąrašą ir atspausdinkime kiekvieno mazgo duomenis. Norėdami pereiti, parašykite bendros paskirties funkciją printList(), kuri spausdina bet kurį nurodytą sąrašą.

# A simple Python program for traversal of a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # This function prints contents of linked list # starting from head def printList(self): temp = self.head while (temp): print (temp.data) temp = temp.next # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3) llist.head.next = second; # Link first node with second second.next = third; # Link second node with the third node llist.printList()>

1 2 3>

Daugiau straipsnių nuorodų sąraše

• Susieto sąrašo įterpimas
• Susieto sąrašo ištrynimas (duoto rakto ištrynimas)
• Susieto sąrašo ištrynimas (rakto ištrynimas nurodytoje padėtyje)
• Raskite susieto sąrašo ilgį (iteratyvus ir rekursyvus)
• Ieškoti elemento susietajame sąraše (iteratyvus ir rekursyvus)
• N-asis mazgas nuo susieto sąrašo pabaigos
• Apverskite susietą sąrašą

A krūva yra linijinė duomenų struktūra, kurioje elementai saugomi paskutinio įvedimo/pirmo išvežimo (LIFO) arba pirmojo įvedimo/paskutinės išvežimo (FILO) būdu. Į krūvą naujas elementas pridedamas viename gale, o elementas pašalinamas tik iš to galo. Įterpimo ir ištrynimo operacijos dažnai vadinamos push ir pop.

stack = [] # append() function to push # element in the stack stack.append('g') stack.append('f') stack.append('g') print('Initial stack') print(stack) # pop() function to pop # element from stack in # LIFO order print('
Elements popped from stack:') print(stack.pop()) print(stack.pop()) print(stack.pop()) print('
Stack after elements are popped:') print(stack) # uncommenting print(stack.pop()) # will cause an IndexError # as the stack is now empty>

Initial stack ['g', 'f', 'g'] Elements popped from stack: g f g Stack after elements are popped: []>

Kaip krūva, eilė yra linijinė duomenų struktūra, kurioje elementai saugomi FIFO (First In First Out) būdu. Esant eilei, pirmiausia pašalinamas mažiausiai neseniai pridėtas elementas. Geras eilės pavyzdys yra bet kokia vartotojų eilė prie išteklių, kur pirmasis aptarnaujamas vartotojas, kuris buvo pirmasis.

datos formatas.formatas

# Initializing a queue queue = [] # Adding elements to the queue queue.append('g') queue.append('f') queue.append('g') print('Initial queue') print(queue) # Removing elements from the queue print('
Elements dequeued from queue') print(queue.pop(0)) print(queue.pop(0)) print(queue.pop(0)) print('
Queue after removing elements') print(queue) # Uncommenting print(queue.pop(0)) # will raise and IndexError # as the queue is now empty>

Initial queue ['g', 'f', 'g'] Elements dequeued from queue g f g Queue after removing elements []>

Prioritetinės eilės yra abstrakčios duomenų struktūros, kuriose kiekvienas eilės duomenims/reikšmei suteikiamas tam tikras prioritetas. Pavyzdžiui, oro linijose bagažas, pavadintas Verslo arba Pirmos klasės, atkeliauja anksčiau nei kiti. Prioritetinė eilė yra eilės plėtinys su šiomis savybėmis.

• Aukšto prioriteto elementas ištraukiamas prieš elementą, kurio prioritetas žemas.
• Jei du elementai turi tą patį prioritetą, jie pateikiami pagal eilę.

# A simple implementation of Priority Queue # using Queue. class PriorityQueue(object): def __init__(self): self.queue = [] def __str__(self): return ' '.join([str(i) for i in self.queue]) # for checking if the queue is empty def isEmpty(self): return len(self.queue) == 0 # for inserting an element in the queue def insert(self, data): self.queue.append(data) # for popping an element based on Priority def delete(self): try: max = 0 for i in range(len(self.queue)): if self.queue[i]>self.queue[max]: max = i item = self.queue[max] del self.queue[max] grąžinti elementą, išskyrus IndexError: print() exit() if __name__ == '__main__': myQueue = PriorityQueue( ) myQueue.insert(12) myQueue.insert(1) myQueue.insert(14) myQueue.insert(7) print(myQueue), o ne myQueue.isEmpty(): print(myQueue.delete())>

12 1 14 7 14 12 7 1>

Krūva

heapq modulis Python pateikia krūvos duomenų struktūrą, kuri daugiausia naudojama prioritetinei eilei atstovauti. Šios duomenų struktūros savybė yra ta, kad ji visada pateikia mažiausią elementą (min. krūvą), kai elementas iššokamas. Kai elementai stumiami arba iššokami, krūvos struktūra išlaikoma. Elementas heap[0] kiekvieną kartą taip pat grąžina mažiausią elementą. Tai palaiko mažiausio elemento ištraukimą ir įterpimą per O (log n) laikus.

Paprastai krūvos gali būti dviejų tipų:

• Didžiausia krūva: „Max-Heap“ šakniniame mazge esantis raktas turi būti didžiausias tarp visų jo antrinių raktų. Ta pati savybė turi būti rekursyviai teisinga visiems to dvejetainio medžio submedžiams.
• Min-Heap: „Min-Heap“ šakniniame mazge esantis raktas turi būti minimalus tarp visų antrinių raktų. Ta pati savybė turi būti rekursyviai teisinga visiems to dvejetainio medžio submedžiams.

# importing 'heapq' to implement heap queue import heapq # initializing list li = [5, 7, 9, 1, 3] # using heapify to convert list into heap heapq.heapify(li) # printing created heap print ('The created heap is : ',end='') print (list(li)) # using heappush() to push elements into heap # pushes 4 heapq.heappush(li,4) # printing modified heap print ('The modified heap after push is : ',end='') print (list(li)) # using heappop() to pop smallest element print ('The popped and smallest element is : ',end='') print (heapq.heappop(li))>

The created heap is : [1, 3, 9, 7, 5] The modified heap after push is : [1, 3, 4, 7, 5, 9] The popped and smallest element is : 1>

Daugiau straipsnių apie Heap

• Dvejetainė krūva
• K-asis didžiausias masyvo elementas
• K'th mažiausias / didžiausias nerūšiuoto masyvo elementas
• Rūšiuoti beveik surūšiuotą masyvą
• K-asis didžiausios sumos gretimas pogrupis
• Mažiausia dviejų skaičių suma, sudaryta iš masyvo skaitmenų

Medis yra hierarchinė duomenų struktūra, kuri atrodo taip, kaip paveikslėlyje žemiau –

 tree  ----  j <-- root  /   f k  /   a h z <-- leaves>

Viršutinis medžio mazgas vadinamas šakniu, o apatiniai mazgai arba mazgai be vaikų vadinami lapų mazgais. Mazgai, esantys tiesiai po mazgu, vadinami jo vaikais, o mazgai, esantys tiesiai virš kažko, vadinami pirminiais.

A dvejetainis medis yra medis, kurio elementai gali turėti beveik du vaikus. Kadangi kiekvienas dvejetainio medžio elementas gali turėti tik 2 vaikus, paprastai juos pavadiname kairiuoju ir dešiniuoju vaikais. Dvejetainio medžio mazgą sudaro šios dalys.

• Duomenys
• Rodyklė į kairį vaiką
• Nukreipkite į tinkamą vaiką

Pavyzdys: Mazgo klasės apibrėžimas

# A Python class that represents an individual node # in a Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key>

Dabar „Python“ sukurkime medį su 4 mazgais. Tarkime, kad medžio struktūra atrodo taip:

 tree  ----  1 <-- root  /   2 3   /  4>

Pavyzdys: duomenų įtraukimas į medį

# Python program to introduce Binary Tree # A class that represents an individual node in a # Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key # create root root = Node(1) ''' following is the tree after above statement  1  /   None None''' root.left = Node(2); root.right = Node(3); ''' 2 and 3 become left and right children of 1  1  /   2 3  /  /  None None None None''' root.left.left = Node(4); '''4 becomes left child of 2  1  /   2 3  /  /  4 None None None /  None None'''>

Medžių perėjimas

Medžius galima pervažiuoti įvairiais būdais. Toliau pateikiami dažniausiai naudojami medžių kirtimo būdai. Panagrinėkime žemiau esantį medį -

 tree  ----  1 <-- root  /   2 3   /  4 5>

Pirmosios kelionės gyliu:

• Eilė (kairė, šaknis, dešinė): 4 2 5 1 3
• Išankstinis užsakymas (šaknis, kairė, dešinė): 1 2 4 5 3
• Postorder (kairėje, dešinėje, šaknyje): 4 5 2 3 1

Algoritmo eilės tvarka (medis)

• Pereikite kairįjį pomedį, t. y. iškvieskite Inorder(left-submedis)
• Aplankykite šaknį.
• Pereikite dešinįjį pomedį, t. y. iškvieskite Inorder (dešinė-submedis)

Algoritmo išankstinis užsakymas (medis)

• Aplankykite šaknį.
• Pereikite kairįjį pomedį, t. y. iškvieskite išankstinį užsakymą (left-submedis)
• Pereikite dešinįjį pomedį, t. y. iškvieskite išankstinį užsakymą (dešinė-submedis)

Algoritmas Pašto orderis (medis)

• Pereikite kairįjį pomedį, t. y. iškvieskite Postorder(left-submedis)
• Pereikite dešinįjį pomedį, t. y. iškvieskite Postorder (dešinysis pomedis)
• Aplankykite šaknį.

# Python program to for tree traversals # A class that represents an individual node in a # Binary Tree class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A function to do inorder tree traversal def printInorder(root): if root: # First recur on left child printInorder(root.left) # then print the data of node print(root.val), # now recur on right child printInorder(root.right) # A function to do postorder tree traversal def printPostorder(root): if root: # First recur on left child printPostorder(root.left) # the recur on right child printPostorder(root.right) # now print the data of node print(root.val), # A function to do preorder tree traversal def printPreorder(root): if root: # First print the data of node print(root.val), # Then recur on left child printPreorder(root.left) # Finally recur on right child printPreorder(root.right) # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print('Preorder traversal of binary tree is') printPreorder(root) print('
Inorder traversal of binary tree is') printInorder(root) print('
Postorder traversal of binary tree is') printPostorder(root)>

Preorder traversal of binary tree is 1 2 4 5 3 Inorder traversal of binary tree is 4 2 5 1 3 Postorder traversal of binary tree is 4 5 2 3 1>

Laiko sudėtingumas – O(n)

Pirmojo arba lygio užsakymo praėjimas

Lygio užsakymo perėjimas medžio yra pločio pirmas medžio apvažiavimas. Aukščiau pateikto medžio lygio eilės tvarka yra 1 2 3 4 5.

Kiekviename mazge pirmiausia aplankomas mazgas, o tada jo antriniai mazgai įtraukiami į FIFO eilę. Žemiau yra to paties algoritmas -

• Sukurkite tuščią eilę q
• temp_node = root /*pradėti nuo šaknies*/
• Ciklas, kol temp_node nėra NULL
  • spausdinti temp_node->data.
  • Į eilę įrašykite temp_node vaikus (pirma kairėje, tada dešinėje) į q
  • Nuimkite mazgą iš q

# Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self ,key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # Spausdinkite eilės priekį ir # pašalinkite jį iš eilės print (queue[0].data) node = queue.pop(0) # Į eilę palikti antrinį, jei node.left nėra Nėra: queue.append(node.left ) # Įrašykite dešinįjį antrinį eilę, jei node.right nėra Nėra: queue.append(node.right) # Tvarkyklės programa, skirta patikrinti aukščiau pateiktą funkciją root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Mazgas(4) root.left.right = Mazgas(5) print ('Lygio tvarka Dvejetainio medžio apžiūra yra -') printLevelOrder(root)>

Level Order Traversal of binary tree is - 1 2 3 4 5>

Laiko sudėtingumas: O(n)

Daugiau straipsnių apie dvejetainį medį

• Įterpimas į dvejetainį medį
• Ištrynimas dvejetainiame medyje
• Inorder Tree Traversation be rekursijos
• Inorder Tree Traversal be rekursijos ir be krūvos!
• Spausdinti Postorder traversal iš nurodytų Inorder ir Preorder traversals
• Raskite BST postorder traversal iš išankstinio užsakymo perėjimo

Dvejetainis paieškos medis yra mazgu pagrįsta dvejetainio medžio duomenų struktūra, turinti šias savybes:

# A utility function to search a given key in BST def search(root,key): # Base Cases: root is null or key is present at root if root is None or root.val == key: return root # Key is greater than root's key if root.val < key: return search(root.right,key) # Key is smaller than root's key return search(root.left,key)>

# Python program to demonstrate # insert operation in binary search tree # A utility class that represents # an individual node in a BST class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A utility function to insert # a new node with the given key def insert(root, key): if root is None: return Node(key) else: if root.val == key: return root elif root.val < key: root.right = insert(root.right, key) else: root.left = insert(root.left, key) return root # A utility function to do inorder tree traversal def inorder(root): if root: inorder(root.left) print(root.val) inorder(root.right) # Driver program to test the above functions # Let us create the following BST # 50 # /  # 30 70 # /  /  # 20 40 60 80 r = Node(50) r = insert(r, 30) r = insert(r, 20) r = insert(r, 40) r = insert(r, 70) r = insert(r, 60) r = insert(r, 80) # Print inorder traversal of the BST inorder(r)>

20 30 40 50 60 70 80>

A grafiką yra netiesinė duomenų struktūra, susidedanti iš mazgų ir briaunų. Mazgai kartais taip pat vadinami viršūnėmis, o kraštai yra linijos arba lankai, jungiantys bet kuriuos du grafiko mazgus. Formaliau grafiką galima apibrėžti kaip grafiką, susidedantį iš baigtinės viršūnių (arba mazgų) rinkinio ir briaunų, jungiančių mazgų porą, rinkinio.

# A simple representation of graph using Adjacency Matrix class Graph: def __init__(self,numvertex): self.adjMatrix = [[-1]*numvertex for x in range(numvertex)] self.numvertex = numvertex self.vertices = {} self.verticeslist =[0]*numvertex def set_vertex(self,vtx,id): if 0<=vtx<=self.numvertex: self.vertices[id] = vtx self.verticeslist[vtx] = id def set_edge(self,frm,to,cost=0): frm = self.vertices[frm] to = self.vertices[to] self.adjMatrix[frm][to] = cost # for directed graph do not add this self.adjMatrix[to][frm] = cost def get_vertex(self): return self.verticeslist def get_edges(self): edges=[] for i in range (self.numvertex): for j in range (self.numvertex): if (self.adjMatrix[i][j]!=-1): edges.append((self.verticeslist[i],self.verticeslist[j],self.adjMatrix[i][j])) return edges def get_matrix(self): return self.adjMatrix G =Graph(6) G.set_vertex(0,'a') G.set_vertex(1,'b') G.set_vertex(2,'c') G.set_vertex(3,'d') G.set_vertex(4,'e') G.set_vertex(5,'f') G.set_edge('a','e',10) G.set_edge('a','c',20) G.set_edge('c','b',30) G.set_edge('b','e',40) G.set_edge('e','d',50) G.set_edge('f','e',60) print('Vertices of Graph') print(G.get_vertex()) print('Edges of Graph') print(G.get_edges()) print('Adjacency Matrix of Graph') print(G.get_matrix())>

Grafo viršūnės

[„a“, „b“, „c“, „d“, „e“, „f“]

Grafo kraštai

pagrindinis metodas java

[('a', 'c', 20), ('a', 'e', 10), ('b', 'c', 30), ('b', 'e', 40), ( „c“, „a“, 20), („c“, „b“, 30), („d“, „e“, 50), („e“, „a“, 10), („e“ ', 'b', 40), ('e', 'd', 50), ('e', 'f', 60), ('f', 'e', ​​60)]

Grafo gretimų matrica

[[-1, -1, 20, -1, 10, -1], [-1, -1, 30, -1, 40, -1], [20, 30, -1, -1, -1 , -1], [-1, -1, -1, -1, 50, -1], [10, 40, -1, 50, -1, 60], [-1, -1, -1, -1, 60, -1]]

Gretimų sąrašas

Naudojamas sąrašų masyvas. Masyvo dydis lygus viršūnių skaičiui. Tegul masyvas yra masyvas []. Įvesties masyvas [i] reiškia viršūnių, esančių greta i-osios viršūnės, sąrašą. Šis vaizdas taip pat gali būti naudojamas svertiniam grafikui pavaizduoti. Kraštų svoriai gali būti pavaizduoti kaip porų sąrašai. Toliau pateikiamas aukščiau esančios diagramos gretimų vietų sąrašo vaizdas.

# A class to represent the adjacency list of the node class AdjNode: def __init__(self, data): self.vertex = data self.next = None # A class to represent a graph. A graph # is the list of the adjacency lists. # Size of the array will be the no. of the # vertices 'V' class Graph: def __init__(self, vertices): self.V = vertices self.graph = [None] * self.V # Function to add an edge in an undirected graph def add_edge(self, src, dest): # Adding the node to the source node node = AdjNode(dest) node.next = self.graph[src] self.graph[src] = node # Adding the source node to the destination as # it is the undirected graph node = AdjNode(src) node.next = self.graph[dest] self.graph[dest] = node # Function to print the graph def print_graph(self): for i in range(self.V): print('Adjacency list of vertex {}
 head'.format(i), end='') temp = self.graph[i] while temp: print(' ->{}'.format(temp.vertex), end='') temp = temp.next print(' 
') # Tvarkyklės programa aukščiau nurodytai grafiko klasei if __name__ == '__main__' : V = 5 graph = Graph(V) graph.add_edge(0, 1) graph.add_dge(0, 4) graph.add_dge(1, 2) graph.add_dge(1, 3) graph.add_dge(1, 4) graph.add_edge(2, 3) graph.add_edge(3, 4) graph.print_graph()>

Adjacency list of vertex 0 head ->4 -> 1 viršūnių gretimų sąrašas 1 galva -> 4 -> 3 -> 2 -> 0 gretimų viršūnių sąrašas 2 galva -> 3 -> 1 gretimų viršūnių sąrašas 3 galva -> 4 -> 2 -> 1 gretimų viršūnių sąrašas viršūnių sąrašas 4 galva -> 3 -> 1 -> 0>> 
Grafiko perėjimas
Breadth-First Search arba BFS
 
    Breadth-First Traversal  nes grafikas yra panašus į medžio pločio apėjimą. Vienintelis dalykas yra tas, kad skirtingai nei medžiuose, diagramose gali būti ciklai, todėl galime vėl patekti į tą patį mazgą. Kad mazgas nebūtų apdorotas daugiau nei vieną kartą, naudojame loginį aplankytą masyvą. Paprastumo dėlei daroma prielaida, kad visos viršūnės pasiekiamos iš pradinės viršūnės.
 
Pavyzdžiui, sekančiame grafe pradedame ėjimą nuo 2 viršūnės. Kai pasiekiame viršūnę 0, ieškome visų gretimų jos viršūnių. 2 taip pat yra gretima viršūnė, lygi 0. Jei nepažymėsime aplankytų viršūnių, tada 2 bus apdorojamas dar kartą ir tai taps nesibaigiančiu procesu. Šios grafikos skersmuo pirmas plotis yra 2, 0, 3, 1.
 
  
Python3 
# Python3 Program to print BFS traversal # from a given source vertex. BFS(int s) # traverses vertices reachable from s. from collections import defaultdict # This class represents a directed graph # using adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self,u,v): self.graph[u].append(v) # Function to print a BFS of graph def BFS(self, s): # Mark all the vertices as not visited visited = [False] * (max(self.graph) + 1) # Create a queue for BFS queue = [] # Mark the source node as # visited and enqueue it queue.append(s) visited[s] = True while queue: # Dequeue a vertex from # queue and print it s = queue.pop(0) print (s, end = ' ') # Get all adjacent vertices of the # dequeued vertex s. If a adjacent # has not been visited, then mark it # visited and enqueue it for i in self.graph[s]: if visited[i] == False: queue.append(i) visited[i] = True # Driver code # Create a graph given in # the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print ('Following is Breadth First Traversal' ' (starting from vertex 2)') g.BFS(2)>
   
  Išvestis  Laiko sudėtingumas: O(V+E), kur V – grafo viršūnių skaičius, o E – grafo briaunų skaičius.
 
Pirmoji gilumo paieška arba DFS
  Pirmasis gylis  nes grafikas yra panašus į medžio gylio pirmąjį apėjimą. Vienintelis dalykas čia yra tas, kad skirtingai nei medžiai, diagramose gali būti ciklai, mazgas gali būti aplankytas du kartus. Kad mazgas nebūtų apdorotas daugiau nei vieną kartą, naudokite loginį aplankytą masyvą.
 
    Algoritmas:    
 
Sukurkite rekursinę funkciją, kuri paima mazgo ir aplankyto masyvo indeksą.
Pažymėkite dabartinį mazgą kaip aplankytą ir atspausdinkite mazgą.
Pereikite visus gretimus ir nepažymėtus mazgus ir iškvieskite rekursinę funkciją su gretimo mazgo indeksu.
Python3 
# Python3 program to print DFS traversal # from a given graph from collections import defaultdict # This class represents a directed graph using # adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self, u, v): self.graph[u].append(v) # A function used by DFS def DFSUtil(self, v, visited): # Mark the current node as visited # and print it visited.add(v) print(v, end=' ') # Recur for all the vertices # adjacent to this vertex for neighbour in self.graph[v]: if neighbour not in visited: self.DFSUtil(neighbour, visited) # The function to do DFS traversal. It uses # recursive DFSUtil() def DFS(self, v): # Create a set to store visited vertices visited = set() # Call the recursive helper function # to print DFS traversal self.DFSUtil(v, visited) # Driver code # Create a graph given # in the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print('Following is DFS from (starting from vertex 2)') g.DFS(2)>
   
  Išvestis  
Following is DFS from (starting from vertex 2) 2 0 1 3>
 
Daugiau straipsnių apie grafiką
 Grafikų vaizdavimas naudojant rinkinį ir maišą 
 Grafike raskite motinos viršūnę 
 Iteratyvus gylis pirmoji paieška 
 Suskaičiuokite mazgų skaičių tam tikrame medžio lygyje naudodami BFS 
 Suskaičiuokite visus galimus kelius tarp dviejų viršūnių 
 Procesas, kurio metu funkcija išsikviečia save tiesiogiai arba netiesiogiai, vadinamas rekursija, o atitinkama funkcija vadinama a  rekursinė funkcija . Naudojant rekursinius algoritmus, tam tikras problemas galima išspręsti gana lengvai. Tokių problemų pavyzdžiai yra Hanojaus bokštai (TOH), Inorder/Preorder/Postorder Tree Traversals, DFS of Graph ir kt. 
  
Kokia yra bazinė rekursijos sąlyga?
Rekursyvinėje programoje pateikiamas bazinio atvejo sprendimas ir didesnės problemos sprendimas išreiškiamas mažesniais uždaviniais.
 
def fact(n):  # base case  if (n <= 1)   return 1  else   return n*fact(n-1)>
Aukščiau pateiktame pavyzdyje nustatytas bazinis atvejis, kai n <= 1, ir didesnė skaičiaus reikšmė gali būti išspręsta konvertuojant į mažesnę, kol pasiekiama bazinė raidė.
 
Kaip atmintis paskirstoma skirtingiems funkcijų iškvietimams rekursijos metu?
Kai kuri nors funkcija iškviečiama iš main(), atmintis jai priskiriama krūvoje. Rekursyvinė funkcija iškviečia save, iškviestos funkcijos atmintis paskirstoma virš atminties, skirtos iškvietimo funkcijai, ir kiekvienam funkcijos iškvietimui sukuriama skirtinga vietinių kintamųjų kopija. Pasiekus bazinį atvejį, funkcija grąžina savo reikšmę funkcijai, kuri ją iškviečia, atmintis atimama ir procesas tęsiasi.
 
Paimkime pavyzdį, kaip veikia rekursija, paimdami paprastą funkciją.
Python3 
# A Python 3 program to # demonstrate working of # recursion def printFun(test): if (test < 1): return else: print(test, end=' ') printFun(test-1) # statement 2 print(test, end=' ') return # Driver Code test = 3 printFun(test)>
   
  Išvestis  
3 2 1 1 2 3>
 
Atminties krūva parodyta žemiau esančioje diagramoje.
 
 
 
Daugiau straipsnių apie Rekursiją 
 
 Rekursija  
    Rekursija Python  
 Praktiniai klausimai apie rekursiją | 1 rinkinys 
 Praktiniai klausimai apie rekursiją | 2 rinkinys 
 Praktiniai klausimai apie rekursiją | 3 rinkinys 
 Praktiniai klausimai apie rekursiją | 4 rinkinys 
 Praktiniai klausimai apie rekursiją | 5 rinkinys 
 Praktiniai klausimai apie rekursiją | 6 rinkinys 
 Praktiniai klausimai apie rekursiją | 7 rinkinys 
     >>> Daugiau     
 
    Dinaminis programavimas    
  Dinaminis programavimas  daugiausia yra optimizavimas naudojant paprastą rekursiją. Visur, kur matome rekursyvų sprendimą, kuriame kartojasi tie patys įvesties iškvietimai, galime jį optimizuoti naudodami dinaminį programavimą. Idėja yra tiesiog saugoti subproblemų rezultatus, kad vėliau nereikėtų jų skaičiuoti iš naujo. Šis paprastas optimizavimas sumažina laiko sudėtingumą nuo eksponentinės iki daugianario. Pavyzdžiui, jei Fibonačio skaičiams rašome paprastą rekursinį sprendimą, gauname eksponentinį laiko sudėtingumą, o jei jį optimizuojame išsaugodami subproblemų sprendimus, laiko sudėtingumas sumažėja iki tiesinio.
 
 
 
Lentelių sudarymas prieš atmintį
Yra du skirtingi būdai išsaugoti reikšmes, kad antrinės problemos reikšmes būtų galima panaudoti pakartotinai. Čia bus aptariami du dinaminio programavimo (DP) problemos sprendimo modeliai:
 
    Lentelė:    Iki dugno
    Atmintinė:    Iš viršaus į apačią
Lentelė
Kaip rodo pats pavadinimas, pradėti nuo apačios ir kaupti atsakymus į viršų. Pakalbėkime apie valstybės perėjimą.
 
Apibūdinkime mūsų DP problemos būseną dp[x], o dp[0] kaip bazinę būseną ir dp[n] kaip paskirties būseną. Taigi, turime rasti paskirties būsenos reikšmę, ty dp[n].
 
Jei pradėsime perėjimą nuo savo bazinės būsenos, t. y. dp[0], ir vadovausimės savo būsenos perėjimo ryšiu, kad pasiektume paskirties būseną dp[n], tai vadiname metodu „iš apačios į viršų“, nes visiškai aišku, kad perėjimą pradėjome nuo apatinę bazinę būseną ir pasiekė aukščiausią norimą būseną.
 
Kodėl mes tai vadiname lentelių metodu?
 
Norėdami tai sužinoti, pirmiausia parašykite kodą, kad apskaičiuotumėte skaičiaus faktorialą, naudodami metodą iš apačios į viršų. Vėlgi, kaip bendra DP sprendimo procedūra, pirmiausia apibrėžiame būseną. Šiuo atveju būseną apibrėžiame kaip dp[x], kur dp[x] yra x faktorialas.
 
Dabar visiškai akivaizdu, kad dp[x+1] = dp[x] * (x+1)
 
# Tabulated version to find factorial x. dp = [0]*MAXN # base case dp[0] = 1; for i in range(n+1):  dp[i] = dp[i-1] * i>
Atmintinė
Dar kartą apibūdinkime tai būsenos perėjimo požiūriu. Jei mums reikia rasti kokios nors būsenos reikšmę, pasakykite dp[n] ir vietoj to, kad pradėtume nuo bazinės būsenos, ty dp[0], atsakymo klausiame būsenų, kurios po būsenos perėjimo gali pasiekti paskirties būseną dp[n] santykis, tada tai yra DP mada iš viršaus į apačią.
 
Čia mes pradedame kelionę nuo aukščiausios paskirties būsenos ir apskaičiuojame jos atsakymą, skaičiuodami būsenų, kurios gali pasiekti paskirties būseną, vertes, kol pasiekiame žemiausią bazinę būseną.
 
Dar kartą parašykime faktorinės problemos kodą iš viršaus į apačią
 
# Memoized version to find factorial x. # To speed up we store the values # of calculated states # initialized to -1 dp[0]*MAXN # return fact x! def solve(x):  if (x==0)  return 1  if (dp[x]!=-1)  return dp[x]  return (dp[x] = x * solve(x-1))>
 
 
Daugiau straipsnių apie dinaminį programavimą
 Optimali pagrindo savybė 
 Sutampančių subproblemų savybė 
  Fibonačio skaičiai  
 Poaibis, kurio suma dalijasi iš m 
 Didžiausia suma didėjanti seka 
 Ilgiausia bendroji poeilutė 
      >>> Daugiau      
 
Paieškos algoritmai
Linijinė paieška
Pradėkite nuo kairiojo arr[] elemento ir po vieną palyginkite x su kiekvienu arr[] elementu
Jei x atitinka elementą, grąžinkite indeksą.
Jei x nesutampa su jokiu elementu, grąžinkite -1.
 
  
Python3 
# Python3 code to linearly search x in arr[]. # If x is present then return its location, # otherwise return -1 def search(arr, n, x): for i in range(0, n): if (arr[i] == x): return i return -1 # Driver Code arr = [2, 3, 4, 10, 40] x = 10 n = len(arr) # Function call result = search(arr, n, x) if(result == -1): print('Element is not present in array') else: print('Element is present at index', result)>
   
  Išvestis  
Element is present at index 3>
 
Aukščiau pateikto algoritmo laiko sudėtingumas yra O(n).
 
Norėdami gauti daugiau informacijos, žr Linijinė paieška .
 
Dvejetainė paieška
Ieškokite surūšiuotame masyve pakartotinai padalydami paieškos intervalą per pusę. Pradėkite nuo intervalo, apimančio visą masyvą. Jei paieškos klavišo reikšmė yra mažesnė už elementą intervalo viduryje, susiaurinkite intervalą iki apatinės pusės. Kitu atveju susiaurinkite iki viršutinės pusės. Pakartotinai tikrinkite, kol bus rasta reikšmė arba intervalas bus tuščias.
 
  
Python3 
# Python3 Program for recursive binary search. # Returns index of x in arr if present, else -1 def binarySearch (arr, l, r, x): # Check base case if r>= l: mid = l + (r - l) // 2 # Jei elementas yra pačiame viduryje if arr[mid] == x: return mid # Jei elementas yra mažesnis už vidurį, tada jis # gali būti tik kairiajame pogrupyje elif arr[mid]> x: return binarySearch(arr, l, mid-1, x) # Kitu atveju elementas gali būti tik # dešiniajame poskyryje else: return binarySearch(arr, mid + 1, r, x ) else: # Elemento nėra masyve return -1 # Tvarkyklės kodas arr = [ 2, 3, 4, 10, 40 ] x = 10 # Funkcijos iškvietimo rezultatas = binarySearch(arr, 0, len(arr)-1 , x) if rezultatas != -1: print ('Elementas yra indekse % d' % rezultatas) else: print ('Elemento nėra masyve')>
   
  Išvestis  
Element is present at index 3>
 
Aukščiau pateikto algoritmo laiko sudėtingumas yra O(log(n)).
 
Norėdami gauti daugiau informacijos, žr  Dvejetainė paieška  .
 
Rūšiavimo algoritmai
Pasirinkimas Rūšiuoti
The  atrankos rūšiavimas  algoritmas surūšiuoja masyvą, pakartotinai surasdamas minimalų elementą (atsižvelgiant į didėjančią tvarką) iš nerūšiuotos dalies ir įtraukdamas jį į pradžią. Kiekvienoje atrankos rūšiavimo iteracijoje minimalus elementas (atsižvelgiant į didėjančią tvarką) iš nerūšiuoto pogrupio parenkamas ir perkeliamas į surūšiuotą porūšį.
 
Pasirinkimo rūšiavimo schema:
 
  
Python3 
# Python program for implementation of Selection # Sort import sys A = [64, 25, 12, 22, 11] # Traverse through all array elements for i in range(len(A)): # Find the minimum element in remaining # unsorted array min_idx = i for j in range(i+1, len(A)): if A[min_idx]>A[j]: min_idx = j # Sukeiskite rastą minimalų elementą # pirmuoju elementu A[i], A[min_idx] = A[min_idx], A[i] # Tvarkyklės kodas, kurį norite išbandyti virš spausdinimo ('Sorted array ') i diapazone (len(A)): print('%d' %A[i]),>
   
  Išvestis  
Sorted array 11 12 22 25 64>
 
    Laiko sudėtingumas:    O (n2), nes yra dvi įdėtos kilpos.
 
    Pagalbinė erdvė:    O(1)
 
Burbulų rūšiavimas
  Burbulų rūšiavimas  yra paprasčiausias rūšiavimo algoritmas, kuris veikia pakartotinai keičiant gretimus elementus, jei jie yra neteisinga tvarka.
 
    Iliustracija :    
 
  
Python3 
# Python program for implementation of Bubble Sort def bubbleSort(arr): n = len(arr) # Traverse through all array elements for i in range(n): # Last i elements are already in place for j in range(0, n-i-1): # traverse the array from 0 to n-i-1 # Swap if the element found is greater # than the next element if arr[j]>arr[j+1] : arr[j], arr[j+1] = arr[j+1], arr[j] # Vairuotojo kodas, kurį reikia patikrinti aukščiau arr = [64, 34, 25, 12, 22, 11 , 90] bubbleSort(arr) print ('Rūšiuotas masyvas yra:') for i diapazone(len(arr)): print ('%d' %arr[i]),>
   
  Išvestis  
Sorted array is: 11 12 22 25 34 64 90>
 
    Laiko sudėtingumas:    O (n2)
išankstinio užsakymo pervežimas
 
Įterpimo rūšiavimas
Norėdami rūšiuoti n dydžio masyvą didėjančia tvarka, naudodami  įterpimo rūšiavimas  :
 
Per masyvą kartokite nuo arr[1] iki arr[n].
Palyginkite dabartinį elementą (raktą) su jo pirmtaku.
Jei pagrindinis elementas yra mažesnis nei jo pirmtakas, palyginkite jį su ankstesniais elementais. Perkelkite didesnius elementus viena pozicija aukštyn, kad būtų vietos pakeistam elementui.
    Iliustracija:    
 
  
Python3 
# Python program for implementation of Insertion Sort # Function to do insertion sort def insertionSort(arr): # Traverse through 1 to len(arr) for i in range(1, len(arr)): key = arr[i] # Move elements of arr[0..i-1], that are # greater than key, to one position ahead # of their current position j = i-1 while j>= 0 ir raktas< arr[j] : arr[j + 1] = arr[j] j -= 1 arr[j + 1] = key # Driver code to test above arr = [12, 11, 13, 5, 6] insertionSort(arr) for i in range(len(arr)): print ('% d' % arr[i])>
   
  Išvestis  
 5 6 11 12 13>
 
    Laiko sudėtingumas:    O (n2))
 
Sujungti Rūšiuoti
Kaip „QuickSort“,  Sujungti Rūšiuoti  yra „Skaldyk ir valdyk“ algoritmas. Jis padalija įvesties masyvą į dvi dalis, vadinasi dviem pusėms, o tada sujungia dvi surūšiuotas puses. Funkcija merge() naudojama dviejų dalių sujungimui. Sujungimas (arr, l, m, r) yra pagrindinis procesas, kuriame daroma prielaida, kad arr[l..m] ir arr[m+1..r] yra surūšiuoti ir sujungia du surūšiuotus pomasyvius į vieną.
 
MergeSort(arr[], l, r) If r>l 1. Raskite vidurinį tašką, kad padalintumėte masyvą į dvi dalis: vidurinė m = l+ (r-l)/2 2. Skambinti mergeSort pirmajai pusei: Skambinti mergeSort(arr, l, m) 3. Skambinti mergeRūšiuoti antrąją pusę: Skambinti mergeSort(arr, m+1, r) 4. Sujunkite dvi dalis, surūšiuotas 2 ir 3 veiksme: iškvieskite merge(arr, l, m, r)>
 
  
Python3 
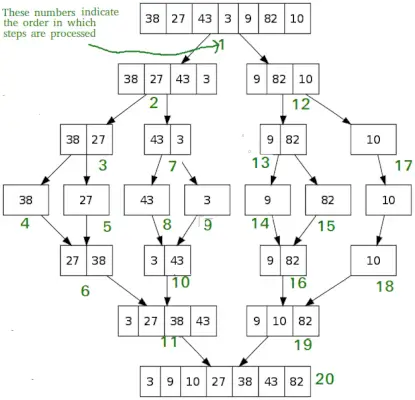
# Python program for implementation of MergeSort def mergeSort(arr): if len(arr)>1: # Masyvo vidurio radimas mid = len(arr)//2 # Masyvo elementų L = arr[:mid] # padalijimas į 2 dalis R = arr[mid:] # Pirmosios pusės rūšiavimas mergeSort(L) # Antrosios pusės rūšiavimas mergeSort(R) i = j = k = 0 # Nukopijuokite duomenis į laikinuosius masyvus L[] ir R[], kol i< len(L) and j < len(R): if L[i] < R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 # Checking if any element was left while i < len(L): arr[k] = L[i] i += 1 k += 1 while j < len(R): arr[k] = R[j] j += 1 k += 1 # Code to print the list def printList(arr): for i in range(len(arr)): print(arr[i], end=' ') print() # Driver Code if __name__ == '__main__': arr = [12, 11, 13, 5, 6, 7] print('Given array is', end='
') printList(arr) mergeSort(arr) print('Sorted array is: ', end='
') printList(arr)>
   
  Išvestis  
Given array is 12 11 13 5 6 7 Sorted array is: 5 6 7 11 12 13>
 
    Laiko sudėtingumas:    O(n(logn))
 
Greitas rūšiavimas
Kaip sujungti rūšiavimą,  Greitas rūšiavimas  yra „Skaldyk ir valdyk“ algoritmas. Jis pasirenka elementą kaip sukimosi tašką ir padalija nurodytą masyvą aplink pasirinktą sukimąsi. Yra daug skirtingų „quickSort“ versijų, kurios parenkamos įvairiais būdais.
 
Pirmąjį elementą visada pasirinkite kaip sukimąsi.
 
Visada pasirinkite paskutinį elementą kaip sukimąsi (įgyvendinta toliau)
Pasirinkite atsitiktinį elementą kaip suvestinę.
Pasirinkite medianą kaip sukimąsi.
Pagrindinis greitojo rūšiavimo procesas yra partition (). Skyrių tikslas yra, jei masyvo masyvas ir masyvo elementas x kaip sukimosi taškas, įdėkite x į teisingą vietą surūšiuotame masyve ir visus mažesnius elementus (mažesnius nei x) sudėkite prieš x, o visus didesnius elementus (didesnius nei x) įdėkite po jo. x. Visa tai turėtų būti daroma tiesiniu laiku.
 
/* low -->Pradinis indeksas, aukštas --> Pabaigos indeksas */ quickSort(arr[], žemas, aukštas) { if (žemas { /* pi yra skaidymo indeksas, arr[pi] dabar yra tinkamoje vietoje */ pi = skaidinys(arr, žemas, aukštas);
 
 
    Padalijimo algoritmas    
 
Gali būti daug būdų, kaip skaidyti, sekti  pseudo kodas  taiko CLRS knygoje pateiktą metodą. Logika paprasta, pradedame nuo kairiojo elemento ir stebime mažesnių (arba lygių) elementų indeksą kaip i. Važiuodami, jei randame mažesnį elementą, esamą elementą sukeičiame su arr[i]. Kitu atveju ignoruosime esamą elementą.
  
# Python3 implementation of QuickSort # This Function handles sorting part of quick sort # start and end points to first and last element of # an array respectively def partition(start, end, array): # Initializing pivot's index to start pivot_index = start pivot = array[pivot_index] # This loop runs till start pointer crosses # end pointer, and when it does we swap the # pivot with element on end pointer while start < end: # Increment the start pointer till it finds an # element greater than pivot while start < len(array) and array[start] <= pivot: start += 1 # Decrement the end pointer till it finds an # element less than pivot while array[end]>Pivot: end -= 1 # Jei pradžia ir pabaiga nesusikerta, # sukeiskite pradžios ir pabaigos skaičius if(pradžia< end): array[start], array[end] = array[end], array[start] # Swap pivot element with element on end pointer. # This puts pivot on its correct sorted place. array[end], array[pivot_index] = array[pivot_index], array[end] # Returning end pointer to divide the array into 2 return end # The main function that implements QuickSort def quick_sort(start, end, array): if (start < end): # p is partitioning index, array[p] # is at right place p = partition(start, end, array) # Sort elements before partition # and after partition quick_sort(start, p - 1, array) quick_sort(p + 1, end, array) # Driver code array = [ 10, 7, 8, 9, 1, 5 ] quick_sort(0, len(array) - 1, array) print(f'Sorted array: {array}')>
   
  Išvestis  
Sorted array: [1, 5, 7, 8, 9, 10]>
 
    Laiko sudėtingumas:    O(n(logn))
 
„ShellSort“.
 „ShellSort“. daugiausia yra įterpimo rūšiavimo variantas. Įterpimo rūšiavimo metu elementus perkeliame tik viena pozicija į priekį. Kai elementą reikia pastumti toli į priekį, vyksta daug judesių. ShellSort idėja yra leisti keistis tolimais daiktais. „ShellSort“ masyvą surūšiuojame pagal didelę h reikšmę. Mes nuolat mažiname h reikšmę, kol ji tampa 1. Masyvas yra surūšiuotas h, jei visi kiekvieno h posąraščiaithelementas surūšiuotas.
Python3 
# Python3 program for implementation of Shell Sort def shellSort(arr): gap = len(arr) // 2 # initialize the gap while gap>0: i = 0 j = tarpas # patikrinkite masyvą iš kairės į dešinę # iki paskutinio galimo j indekso, kol j< len(arr): if arr[i]>arr[j]: arr[i],arr[j] = arr[j],arr[i] i += 1 j += 1 # dabar žiūrime atgal iš i-ojo indekso į kairę # keičiame reikšmes, kurios nėra tinkama tvarka. k = i, o k - tarpas> -1: jei arr[k - tarpas]> arr[k]: arr[k-tarpas],arr[k] = arr[k],arr[k-tarpas] k -= 1 tarpas //= 2 # tvarkyklė kodui patikrinti arr2 = [12, 34, 54, 2, 3] print('input array:',arr2) shellSort(arr2) print('sorted array', arr2)>>  
  Išvestis      Laiko sudėtingumas:    O (n2).