DVEJETAINĖ KRŪVA – TECHCODEVIEW.COM - IT PROBLEMOS IR SPRENDIMAI

A Dvejetainė krūva yra pilnas dvejetainis medis kuris naudojamas duomenims efektyviai saugoti, kad pagal jo struktūrą būtų gautas maksimalus arba minimalus elementas.

Dvejetainė krūva yra arba minimali krūva, arba didžiausia krūva. Minimalioje dvejetainėje krūvoje raktas šaknyje turi būti minimalus tarp visų dvejetainėje krūvoje esančių raktų. Ta pati savybė turi rekursyviai galioti visiems dvejetainio medžio mazgams. Max Binary Heap yra panašus į MinHeap.

Min Heap pavyzdžiai:

10 10
/ /
20 100 15 30
/ / /
30 40 50 100 40

Kaip vaizduojama dvejetainė krūva?

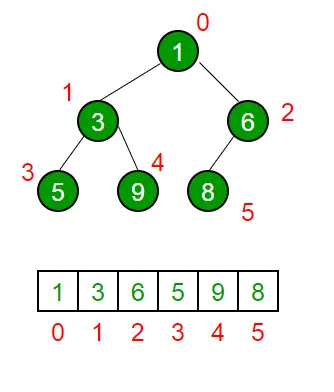
Dvejetainė krūva yra a Pilnas dvejetainis medis . Dvejetainė krūva paprastai vaizduojama kaip masyvas.

Šakninis elementas bus Arr[0].
Žemiau esančioje lentelėje rodomi kitų i mazgų indeksai^thmazgas, ty Arr[i]:

Arr[(i-1)/2]	Grąžina pirminį mazgą
Arr[(2*i)+1]	Grąžina kairįjį antrinį mazgą
Arr[(2*i)+2]	Grąžina tinkamą antrinį mazgą

Perėjimo metodas naudojamas masyvo atvaizdavimui pasiekti Lygio tvarka . Prašau kreiptis į Dvejetainės krūvos masyvas dėl detalių.

Dvejetainis krūvos medis

Operacijos su kaupu:

Žemiau pateikiamos kai kurios standartinės operacijos su minimaliu krūvu:

getMin(): Tai grąžina pagrindinį Min Heap elementą. Laikas Šios operacijos sudėtingumas yra O(1) . Didžiausio krūvos atveju taip būtų getMax () .
ekstraktasMin() : Pašalina minimalų elementą iš MinHeap. Šios operacijos sudėtingumo laikas yra O(log N) nes ši operacija turi išlaikyti krūvos nuosavybę (skambinant kupinti () ) pašalinus šaknį.
MažinimoKey() : Sumažina rakto vertę. Šios operacijos laiko sudėtingumas yra O(log N) . Jei sumažėjusi mazgo rakto reikšmė yra didesnė už pirminį mazgo raktą, nieko daryti nereikia. Priešingu atveju turime važiuoti aukštyn, kad pataisytume pažeistą krūvos ypatybę.
Įdėti() : Naujo rakto įdėjimas užtrunka O(log N) laikas. Medžio gale pridedame naują raktą. Jei naujasis raktas yra didesnis nei jo pirminis raktas, mums nieko daryti nereikia. Priešingu atveju turime važiuoti aukštyn, kad pataisytume pažeistą krūvos ypatybę.
Ištrinti() : Taip pat reikia ištrinti raktą O(log N) laikas. Raktą, kurį reikia ištrinti, pakeičiame į minimalų begalinį skambindami MažinimoKey() . Po dropKey() minus begalinė reikšmė turi pasiekti šaknį, todėl mes iškviečiame ekstraktasMin() norėdami išimti raktą.

Žemiau pateikiamas pagrindinių krūvos operacijų įgyvendinimas.

C++

// A C++ program to demonstrate common Binary Heap Operations> #include> #include> using> namespace> std;> > // Prototype of a utility function to swap two integers> void> swap(>int> *x,>int> *y);> > // A class for Min Heap> class> MinHeap> {> >int> *harr;>// pointer to array of elements in heap> >int> capacity;>// maximum possible size of min heap> >int> heap_size;>// Current number of elements in min heap> public>:> >// Constructor> >MinHeap(>int> capacity);> > >// to heapify a subtree with the root at given index> >void> MinHeapify(>int> i);> > >int> parent(>int> i) {>return> (i-1)/2; }> > >// to get index of left child of node at index i> >int> left(>int> i) {>return> (2*i + 1); }> > >// to get index of right child of node at index i> >int> right(>int> i) {>return> (2*i + 2); }> > >// to extract the root which is the minimum element> >int> extractMin();> > >// Decreases key value of key at index i to new_val> >void> decreaseKey(>int> i,>int> new_val);> > >// Returns the minimum key (key at root) from min heap> >int> getMin() {>return> harr[0]; }> > >// Deletes a key stored at index i> >void> deleteKey(>int> i);> > >// Inserts a new key 'k'> >void> insertKey(>int> k);> };> > // Constructor: Builds a heap from a given array a[] of given size> MinHeap::MinHeap(>int> cap)> {> >heap_size = 0;> >capacity = cap;> >harr =>new> int>[cap];> }> > // Inserts a new key 'k'> void> MinHeap::insertKey(>int> k)> {> >if> (heap_size == capacity)> >{> >cout <<>

'
Overflow: Could not insertKey
'>

;> >return>;> >}> > >// First insert the new key at the end> >heap_size++;> >int> i = heap_size - 1;> >harr[i] = k;> > >// Fix the min heap property if it is violated> >while> (i != 0 && harr[parent(i)]>harr[i])>> {> >swap(&harr[i], &harr[parent(i)]);> >i = parent(i);> >}> }> > // Decreases value of key at index 'i' to new_val. It is assumed that> // new_val is smaller than harr[i].> void> MinHeap::decreaseKey(>int> i,>int> new_val)> {> >harr[i] = new_val;> >while> (i != 0 && harr[parent(i)]>harr[i])>> {> >swap(&harr[i], &harr[parent(i)]);> >i = parent(i);> >}> }> > // Method to remove minimum element (or root) from min heap> int> MinHeap::extractMin()> {> >if> (heap_size <= 0)> >return> INT_MAX;> >if> (heap_size == 1)> >{> >heap_size--;> >return> harr[0];> >}> > >// Store the minimum value, and remove it from heap> >int> root = harr[0];> >harr[0] = harr[heap_size-1];> >heap_size--;> >MinHeapify(0);> > >return> root;> }> > > // This function deletes key at index i. It first reduced value to minus> // infinite, then calls extractMin()> void> MinHeap::deleteKey(>int> i)> {> >decreaseKey(i, INT_MIN);> >extractMin();> }> > // A recursive method to heapify a subtree with the root at given index> // This method assumes that the subtrees are already heapified> void> MinHeap::MinHeapify(>int> i)> {> >int> l = left(i);> >int> r = right(i);> >int> smallest = i;> >if>

(l   smallest = l;   if (r   smallest = r;   if (smallest != i)   {   swap(&harr[i], &harr[smallest]);   MinHeapify(smallest);   }  }    // A utility function to swap two elements  void swap(int *x, int *y)  {   int temp = *x;   *x = *y;   *y = temp;  }    // Driver program to test above functions  int main()  {   MinHeap h(11);   h.insertKey(3);   h.insertKey(2);   h.deleteKey(1);   h.insertKey(15);   h.insertKey(5);   h.insertKey(4);   h.insertKey(45);   cout << h.extractMin() << ' ';   cout << h.getMin() << ' ';   h.decreaseKey(2, 1);   cout << h.getMin();   return 0;  }>

ką tai reiškia xd

Java

// Java program for the above approach> import> java.util.*;> > // A class for Min Heap> class> MinHeap {> > >// To store array of elements in heap> >private> int>[] heapArray;> > >// max size of the heap> >private> int> capacity;> > >// Current number of elements in the heap> >private> int> current_heap_size;> > >// Constructor> >public> MinHeap(>int> n) {> >capacity = n;> >heapArray =>new> int>[capacity];> >current_heap_size =>0>;> >}> > >// Swapping using reference> >private> void> swap(>int>[] arr,>int> a,>int> b) {> >int> temp = arr[a];> >arr[a] = arr[b];> >arr[b] = temp;> >}> > > >// Get the Parent index for the given index> >private> int> parent(>int> key) {> >return> (key ->1>) />2>;> >}> > >// Get the Left Child index for the given index> >private> int> left(>int> key) {> >return> 2> * key +>1>;> >}> > >// Get the Right Child index for the given index> >private> int> right(>int> key) {> >return> 2> * key +>2>;> >}> > > >// Inserts a new key> >public> boolean> insertKey(>int> key) {> >if> (current_heap_size == capacity) {> > >// heap is full> >return> false>;> >}> > >// First insert the new key at the end> >int> i = current_heap_size;> >heapArray[i] = key;> >current_heap_size++;> > >// Fix the min heap property if it is violated> >while> (i !=>0>

&& heapArray[i]   swap(heapArray, i, parent(i));   i = parent(i);   }   return true;   }     // Decreases value of given key to new_val.   // It is assumed that new_val is smaller   // than heapArray[key].   public void decreaseKey(int key, int new_val) {   heapArray[key] = new_val;     while (key != 0 && heapArray[key]   swap(heapArray, key, parent(key));   key = parent(key);   }   }     // Returns the minimum key (key at   // root) from min heap   public int getMin() {   return heapArray[0];   }       // Method to remove minimum element   // (or root) from min heap   public int extractMin() {   if (current_heap_size <= 0) {   return Integer.MAX_VALUE;   }     if (current_heap_size == 1) {   current_heap_size--;   return heapArray[0];   }     // Store the minimum value,   // and remove it from heap   int root = heapArray[0];     heapArray[0] = heapArray[current_heap_size - 1];   current_heap_size--;   MinHeapify(0);     return root;   }     // This function deletes key at the   // given index. It first reduced value   // to minus infinite, then calls extractMin()   public void deleteKey(int key) {   decreaseKey(key, Integer.MIN_VALUE);   extractMin();   }     // A recursive method to heapify a subtree   // with the root at given index   // This method assumes that the subtrees   // are already heapified   private void MinHeapify(int key) {   int l = left(key);   int r = right(key);     int smallest = key;   if (l   smallest = l;   }   if (r   smallest = r;   }     if (smallest != key) {   swap(heapArray, key, smallest);   MinHeapify(smallest);   }   }     // Increases value of given key to new_val.   // It is assumed that new_val is greater   // than heapArray[key].   // Heapify from the given key   public void increaseKey(int key, int new_val) {   heapArray[key] = new_val;   MinHeapify(key);   }     // Changes value on a key   public void changeValueOnAKey(int key, int new_val) {   if (heapArray[key] == new_val) {   return;   }   if (heapArray[key]   increaseKey(key, new_val);   } else {   decreaseKey(key, new_val);   }   }  }    // Driver Code  class MinHeapTest {   public static void main(String[] args) {   MinHeap h = new MinHeap(11);   h.insertKey(3);   h.insertKey(2);   h.deleteKey(1);   h.insertKey(15);   h.insertKey(5);   h.insertKey(4);   h.insertKey(45);   System.out.print(h.extractMin() + ' ');   System.out.print(h.getMin() + ' ');     h.decreaseKey(2, 1);   System.out.print(h.getMin());   }  }    // This code is contributed by rishabmalhdijo>

Python

# A Python program to demonstrate common binary heap operations> > # Import the heap functions from python library> from> heapq>import> heappush, heappop, heapify> > # heappop - pop and return the smallest element from heap> # heappush - push the value item onto the heap, maintaining> # heap invarient> # heapify - transform list into heap, in place, in linear time> > # A class for Min Heap> class> MinHeap:> > ># Constructor to initialize a heap> >def> __init__(>self>):> >self>.heap>=> []> > >def> parent(>self>, i):> >return> (i>->1>)>/>2> > ># Inserts a new key 'k'> >def> insertKey(>self>, k):> >heappush(>self>.heap, k)> > ># Decrease value of key at index 'i' to new_val> ># It is assumed that new_val is smaller than heap[i]> >def> decreaseKey(>self>, i, new_val):> >self>.heap[i]>=> new_val> >while>(i !>=> 0> and> self>.heap[>self>.parent(i)]>>>.heap[i]):> ># Swap heap[i] with heap[parent(i)]> >self>.heap[i] ,>self>.heap[>self>.parent(i)]>=> (> >self>.heap[>self>.parent(i)],>self>.heap[i])> > ># Method to remove minimum element from min heap> >def> extractMin(>self>):> >return> heappop(>self>.heap)> > ># This function deletes key at index i. It first reduces> ># value to minus infinite and then calls extractMin()> >def> deleteKey(>self>, i):> >self>.decreaseKey(i,>float>(>'-inf'>))> >self>.extractMin()> > ># Get the minimum element from the heap> >def> getMin(>self>):> >return> self>.heap[>0>]> > # Driver pgoratm to test above function> heapObj>=> MinHeap()> heapObj.insertKey(>3>)> heapObj.insertKey(>2>)> heapObj.deleteKey(>1>)> heapObj.insertKey(>15>)> heapObj.insertKey(>5>)> heapObj.insertKey(>4>)> heapObj.insertKey(>45>)> > print> heapObj.extractMin(),> print> heapObj.getMin(),> heapObj.decreaseKey(>2>,>1>)> print> heapObj.getMin()> > # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

paveldėjimas c++

C#

// C# program to demonstrate common> // Binary Heap Operations - Min Heap> using> System;> > // A class for Min Heap> class> MinHeap{> > // To store array of elements in heap> public> int>[] heapArray{>get>;>set>; }> > // max size of the heap> public> int> capacity{>get>;>set>; }> > // Current number of elements in the heap> public> int> current_heap_size{>get>;>set>; }> > // Constructor> public> MinHeap(>int> n)> {> >capacity = n;> >heapArray =>new> int>[capacity];> >current_heap_size = 0;> }> > // Swapping using reference> public> static> void> Swap(>ref> T lhs,>ref> T rhs)> {> >T temp = lhs;> >lhs = rhs;> >rhs = temp;> }> > // Get the Parent index for the given index> public> int> Parent(>int> key)> {> >return> (key - 1) / 2;> }> > // Get the Left Child index for the given index> public> int> Left(>int> key)> {> >return> 2 * key + 1;> }> > // Get the Right Child index for the given index> public> int> Right(>int> key)> {> >return> 2 * key + 2;> }> > // Inserts a new key> public> bool> insertKey(>int> key)> {> >if> (current_heap_size == capacity)> >{> > >// heap is full> >return> false>;> >}> > >// First insert the new key at the end> >int> i = current_heap_size;> >heapArray[i] = key;> >current_heap_size++;> > >// Fix the min heap property if it is violated> >while> (i != 0 && heapArray[i] <> >heapArray[Parent(i)])> >{> >Swap(>ref> heapArray[i],> >ref> heapArray[Parent(i)]);> >i = Parent(i);> >}> >return> true>;> }> > // Decreases value of given key to new_val.> // It is assumed that new_val is smaller> // than heapArray[key].> public> void> decreaseKey(>int> key,>int> new_val)> {> >heapArray[key] = new_val;> > >while> (key != 0 && heapArray[key] <> >heapArray[Parent(key)])> >{> >Swap(>ref> heapArray[key],> >ref> heapArray[Parent(key)]);> >key = Parent(key);> >}> }> > // Returns the minimum key (key at> // root) from min heap> public> int> getMin()> {> >return> heapArray[0];> }> > // Method to remove minimum element> // (or root) from min heap> public> int> extractMin()> {> >if> (current_heap_size <= 0)> >{> >return> int>.MaxValue;> >}> > >if> (current_heap_size == 1)> >{> >current_heap_size--;> >return> heapArray[0];> >}> > >// Store the minimum value,> >// and remove it from heap> >int> root = heapArray[0];> > >heapArray[0] = heapArray[current_heap_size - 1];> >current_heap_size--;> >MinHeapify(0);> > >return> root;> }> > // This function deletes key at the> // given index. It first reduced value> // to minus infinite, then calls extractMin()> public> void> deleteKey(>int> key)> {> >decreaseKey(key,>int>.MinValue);> >extractMin();> }> > // A recursive method to heapify a subtree> // with the root at given index> // This method assumes that the subtrees> // are already heapified> public> void> MinHeapify(>int> key)> {> >int> l = Left(key);> >int> r = Right(key);> > >int> smallest = key;> >if>

(l   heapArray[l]   {   smallest = l;   }   if (r   heapArray[r]   {   smallest = r;   }     if (smallest != key)   {   Swap(ref heapArray[key],   ref heapArray[smallest]);   MinHeapify(smallest);   }  }    // Increases value of given key to new_val.  // It is assumed that new_val is greater  // than heapArray[key].  // Heapify from the given key  public void increaseKey(int key, int new_val)  {   heapArray[key] = new_val;   MinHeapify(key);  }    // Changes value on a key  public void changeValueOnAKey(int key, int new_val)  {   if (heapArray[key] == new_val)   {   return;   }   if (heapArray[key]   {   increaseKey(key, new_val);   } else  {   decreaseKey(key, new_val);   }  }  }    static class MinHeapTest{    // Driver code  public static void Main(string[] args)  {   MinHeap h = new MinHeap(11);   h.insertKey(3);   h.insertKey(2);   h.deleteKey(1);   h.insertKey(15);   h.insertKey(5);   h.insertKey(4);   h.insertKey(45);     Console.Write(h.extractMin() + ' ');   Console.Write(h.getMin() + ' ');     h.decreaseKey(2, 1);   Console.Write(h.getMin());  }  }    // This code is contributed by  // Dinesh Clinton Albert(dineshclinton)>

Javascript

Java funkcijos

// A class for Min Heap> class MinHeap> {> >// Constructor: Builds a heap from a given array a[] of given size> >constructor()> >{> >this>.arr = [];> >}> > >left(i) {> >return> 2*i + 1;> >}> > >right(i) {> >return> 2*i + 2;> >}> > >parent(i){> >return> Math.floor((i - 1)/2)> >}> > >getMin()> >{> >return> this>.arr[0]> >}> > >insert(k)> >{> >let arr =>this>.arr;> >arr.push(k);> > >// Fix the min heap property if it is violated> >let i = arr.length - 1;> >while> (i>0 && arr[>this>.parent(i)]>arr[i])>> {> >let p =>this>.parent(i);> >[arr[i], arr[p]] = [arr[p], arr[i]];> >i = p;> >}> >}> > >// Decreases value of key at index 'i' to new_val.> >// It is assumed that new_val is smaller than arr[i].> >decreaseKey(i, new_val)> >{> >let arr =>this>.arr;> >arr[i] = new_val;> > >while> (i !== 0 && arr[>this>.parent(i)]>arr[i])>> {> >let p =>this>.parent(i);> >[arr[i], arr[p]] = [arr[p], arr[i]];> >i = p;> >}> >}> > >// Method to remove minimum element (or root) from min heap> >extractMin()> >{> >let arr =>this>.arr;> >if> (arr.length == 1) {> >return> arr.pop();> >}> > >// Store the minimum value, and remove it from heap> >let res = arr[0];> >arr[0] = arr[arr.length-1];> >arr.pop();> >this>.MinHeapify(0);> >return> res;> >}> > > >// This function deletes key at index i. It first reduced value to minus> >// infinite, then calls extractMin()> >deleteKey(i)> >{> >this>.decreaseKey(i,>this>.arr[0] - 1);> >this>.extractMin();> >}> > >// A recursive method to heapify a subtree with the root at given index> >// This method assumes that the subtrees are already heapified> >MinHeapify(i)> >{> >let arr =>this>.arr;> >let n = arr.length;> >if> (n === 1) {> >return>;> >}> >let l =>this>.left(i);> >let r =>this>.right(i);> >let smallest = i;> >if>

(l   smallest = l;   if (r   smallest = r;   if (smallest !== i)   {   [arr[i], arr[smallest]] = [arr[smallest], arr[i]]   this.MinHeapify(smallest);   }   }  }    let h = new MinHeap();   h.insert(3);   h.insert(2);   h.deleteKey(1);   h.insert(15);   h.insert(5);   h.insert(4);   h.insert(45);     console.log(h.extractMin() + ' ');   console.log(h.getMin() + ' ');     h.decreaseKey(2, 1);   console.log(h.extractMin());>

Išvestis

2 4 1>

Krūvų pritaikymas:

Krūvos rūšiavimas : Krūvos rūšiavimas naudoja dvejetainę krūvą, kad surūšiuotų masyvą O(nLogn) laiku.
Prioritetinė eilė: Prioritetinės eilės gali būti efektyviai įdiegtos naudojant dvejetainę krūvą, nes palaiko įterpimo(), trynimo() ir extractmax(), mažėjimoKey() operacijas per O(log N) laiką. Dvejetainė krūva ir Fibonačio krūva yra dvejetainės krūvos variantai. Šie variantai taip pat efektyviai jungiasi.
Grafikų algoritmai: prioritetinės eilės ypač naudojamos grafikų algoritmuose, pvz Dijkstros trumpiausias kelias ir Prim minimalus besitęsiantis medis .
Daugelį problemų galima efektyviai išspręsti naudojant Heaps. Pavyzdžiui, žr. a) K-asis didžiausias masyvo elementas . b) Rūšiuoti beveik surūšiuotą masyvą/ c) Sujungti K rūšiuotus masyvus .

Susijusios nuorodos:

Kodavimo praktika „Heap“.
Visi straipsniai apie Heap
PriorityQueue: dvejetainės krūvos diegimas Java bibliotekoje