Mes žinome a medis yra nelinijinė duomenų struktūra. Vaikų skaičius neribojamas. AKas yra pilnas dvejetainis medis?

Išbaigtas dvejetainis medis yra specialus dvejetainio medžio tipas, kuriame visi medžio lygiai yra užpildyti visiškai, išskyrus žemiausio lygio mazgus, kurie užpildomi kiek įmanoma iš kairės.

Pilnas dvejetainis medis

Kai kurie visiško dvejetainio medžio terminai:

• Šaknis – Mazgas, kuriame nėra krašto iš pirminio. Pavyzdys - mazgas A
• Vaikas – Mazgas, turintis kažkokį įeinantį kraštą, vadinamas vaiku. Pavyzdys – mazgai B, F yra atitinkamai A ir C vaikai.
• Sesuo – Mazgai, turintys tą patį tėvą, yra broliai ir seserys. Pavyzdys – D, E yra broliai ir seserys, nes turi tą patį tėvą B.
• Mazgo laipsnis – konkretaus tėvo vaikų skaičius. Pavyzdys – A laipsnis yra 2, o C laipsnis yra 1. D laipsnis yra 0.
• Vidiniai / išoriniai mazgai – Lapų mazgai yra išoriniai mazgai, o ne lapų mazgai yra vidiniai.
• Lygis – Suskaičiuokite mazgus kelyje, kad pasiektumėte paskirties mazgą. Pavyzdys – mazgo D lygis yra 2, nes mazgai A ir B sudaro kelią.
• Aukštis – Kraštų skaičius, kad būtų pasiektas paskirties mazgas, šaknis yra 0 aukštyje. Pavyzdys – E mazgo aukštis yra 2, nes jis turi dvi briaunas nuo šaknies.

Viso dvejetainio medžio savybės:

• Sakoma, kad pilnas dvejetainis medis yra tinkamas dvinaris medis, kuriame visi lapai yra vienodo gylio.
• Visame dvejetainiame medyje mazgų skaičius gylyje d yra 2 ^d .
• Pilname dvejetainiame medyje su n mazgų aukštis medžio yra log(n+1) .
• Visi lygiai išskyrus paskutinį lygį yra visiškai pilni.

Tobulas dvejetainis medis prieš pilną dvejetainį medį:

Dvejetainis medis, kurio aukštis „h“, turintis didžiausią mazgų skaičių, yra a puikus dvejetainis medis.
Tam tikram aukščiui h , maksimalus mazgų skaičius yra 2 ^h+1 -1 .

A užbaigti h aukščio dvejetainis medis yra puikus dvinaris medis iki aukščio h-1 , o paskutiniame lygyje elementai saugomi iš kairės į dešinę.

1 pavyzdys:

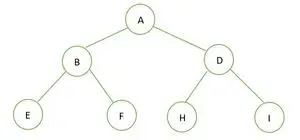
Dvejetainis medis

Pateikto dvejetainio medžio aukštis yra 2, o didžiausias mazgų skaičius tame medyje yra n= 2^h+1-1 = 2²⁺¹-1 = 2³-1 = 7 .
Taigi galime daryti išvadą, kad taip tobulas dvejetainis medis .
Dabar pilnas dvejetainis medis yra pilnas iki aukščio h-1 t.y.; 1, o paskutinio lygio elementai saugomi iš kairės į dešinę. Vadinasi, tai taip pat pilnas dvejetainis medis. Čia yra elementų vaizdavimas, kai jie saugomi masyve

Elementas saugomas masyve lygiu pagal lygį

Masyve visi elementai saugomi nuolat.

2 pavyzdys:

tyčia tyčia

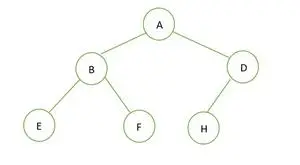
Dvejetainis medis

Pateikto dvejetainio medžio aukštis yra 2, o maksimalus mazgų skaičius, kuris turėtų būti ten, yra 2^h+1– 1 = 2²⁺¹– 1 = 2³– 1 = 7 .
Bet mazgų skaičius medyje yra 6 . Vadinasi, yra nėra tobulas dvejetainis medis .
Dabar pilnas dvejetainis medis yra pilnas iki aukščio h-1 t.y.; 1 , o paskutinis lygio elementas išsaugomas iš kairės į dešinę. Taigi tai yra a pilnas dvejetainis medis . Išsaugokite elementą masyve ir jis bus panašus;

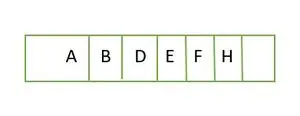
Elementas saugomas masyve lygiu pagal lygį

3 pavyzdys:

oi

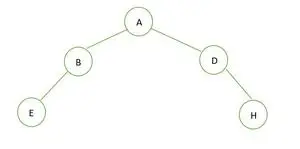
Dvejetainis medis

Dvejetainio medžio aukštis yra 2, o maksimalus mazgų skaičius, kuris jame gali būti, yra 7, tačiau yra tik 5 mazgai, todėl jis yra nėra tobulas dvejetainis medis .
Viso dvejetainio medžio atveju matome, kad paskutiniame lygyje elementai nepildomi iš kairės į dešinę. Taip ir yra nėra pilnas dvejetainis medis .

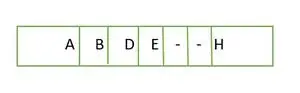
Elementas saugomas masyve lygiu pagal lygį

Masyvo elementai nėra ištisiniai.

Visas dvejetainis medis ir pilnas dvejetainis medis:

Visame dvejetainiame medyje kiekvienas mazgas turi arba 2 vaikus, arba 0 vaikų.

1 pavyzdys:

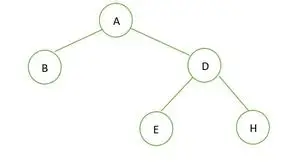
Dvejetainis medis

Pateiktame dvejetainiame medyje nėra 1 laipsnio mazgo, 2 arba 0 vaikų kiekvienam mazgui, todėl jis yra pilnas dvejetainis medis .

Viso dvejetainio medžio elementai saugomi lygiais po lygių, o ne iš kairiosios pusės paskutiniame lygyje. Taigi tai yra nėra pilnas dvejetainis medis . Masyvo vaizdavimas yra toks:

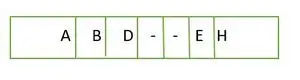
Elementas saugomas masyve lygiu pagal lygį

2 pavyzdys:

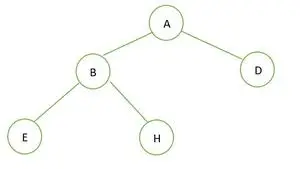
Dvejetainis medis

Pateiktame dvejetainiame medyje nėra mazgo, kurio laipsnis būtų 1. Kiekvienas mazgas turi 2 arba 0 laipsnį. Taigi jis yra pilnas dvejetainis medis .

Viso dvejetainio medžio elementai saugomi lygiu pagal lygį ir užpildomi iš kairiosios paskutinio lygio pusės. Taigi šis a pilnas dvejetainis medis . Žemiau pateikiamas medžio masyvo vaizdas:

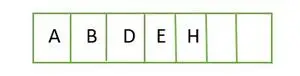
Elementas saugomas masyve lygiu pagal lygį

3 pavyzdys:

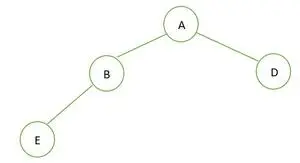
Dvejetainis medis

Pateiktame dvejetainiame medyje mazgas B turi 1 laipsnį, kuris pažeidžia viso dvejetainio medžio savybę, todėl jis yra ne pilnas dvejetainis medis

eilutėje java

Viso dvejetainio medžio elementai saugomi lygiu pagal lygį ir užpildomi iš kairiosios paskutinio lygio pusės. Taigi tai yra a pilnas dvejetainis medis . Dvejetainio medžio masyvo atvaizdavimas yra toks:

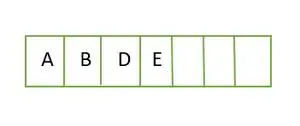
Elementas saugomas masyve lygiu pagal lygį

4 pavyzdys:

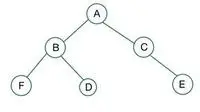
dvejetainis medis

Pateiktame dvejetainio medžio mazgas C turi 1 laipsnį, kuris pažeidžia viso dvejetainio medžio savybę, todėl jis yra ne pilnas dvejetainis medis

Viso dvejetainio medžio elementai saugomi lygiu pagal lygį ir užpildomi iš kairiosios paskutinio lygio pusės. Čia mazgas E pažeidžia sąlygą. Taigi tai yra nėra pilnas dvejetainis medis .

Viso dvejetainio medžio sukūrimas:

Mes žinome a pilnas dvejetainis medis yra medis, kuriame, išskyrus paskutinį lygį (tarkim l )visas kitas lygis turi ( 2l ) mazgai ir mazgai yra išdėstyti iš kairės į dešinę.
Jį galima pavaizduoti naudojant masyvą. Jei tėvas yra tai indeksas i taigi kairysis vaikas yra prie 2i+1 ir tinkamas vaikas yra prie 2i+2 .

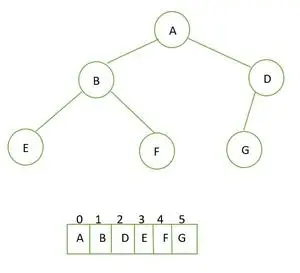
Visas dvejetainis medis ir jo masyvo atvaizdavimas

Algoritmas:

Dėl a Pilnas dvejetainis medis , mums reikia a 1 žingsnis: Kai medis tuščias, inicijuokite šaknį su nauju mazgu.

2 žingsnis: Jei medis nėra tuščias, gaukite priekinį elementą

global var in js

• Jei priekiniame elemente nėra kairiojo vaiko, nustatykite kairįjį antrį į naują mazgą
• Jei tinkamo vaiko nėra, nustatykite tinkamą vaiką kaip naują mazgą

3 veiksmas: Jei mazgas turi abu vaikus, tada pop tai iš eilės.

4 veiksmas: Įdėkite naujus duomenis į eilę.

Iliustracija:

Apsvarstykite toliau pateiktą masyvą:

1. 1-asis elementas bus šaknis (reikšmė indekse = 0 )

A imamas kaip šaknis

2. Kitas elementas (prie indekso = 1 ) bus kairysis ir trečiasis elementas (indeksas = 2 ) bus teisingas šaknies vaikas

B kaip kairysis vaikas, o D kaip dešinysis vaikas

3. ketvirta (indeksas = 3 ) ir penktasis elementas (indeksas = 4 ) bus kairysis ir dešinysis B mazgo antrinis

E ir F yra kairysis ir dešinysis B vaikai

4. Kitas elementas (indeksas = 5 ) bus paliktas mazgo D vaikas

pabandykite gaudyti bloką java

G yra kairysis D mazgo vaikas

Taip sukuriamas pilnas dvejetainis medis.

Įgyvendinimas: Norint sukurti pilną dvejetainį medį iš lygio užsakymo, pateikiamas perėjimas šis įrašas .

Viso dvejetainio medžio taikymas:

• Krūvos rūšiavimas
• Krūvos rūšiavimu pagrįsta duomenų struktūra

Patikrinkite, ar duotas dvejetainis medis yra baigtas, ar ne: Sekite šis įrašas patikrinti, ar pateiktas dvejetainis medis yra baigtas, ar ne.