Daugiakampis matematikoje yra dvimatė forma, sudaryta iš tiesių linijų, kurios sudaro uždarą daugiakampę grandinę. Žodis daugiakampis kilęs iš žodžių poly ir gon, kurie reiškia daug ir pusių.
Daugiakampiai gali būti paprasti arba susikertantys. Paprastas daugiakampis nesusikerta su savimi, išskyrus bendrus iš eilės einančių atkarpų galinius taškus. Daugiakampė grandinė, susikertanti per save, sukuria savaime susikertantį daugiakampį. Daugiakampiai taip pat gali būti klasifikuojami kaip įgaubti arba išgaubti.
Šiame straipsnyje mes išsamiai paminėjome daugiakampius ir jų tipus, formules ir pavyzdžius.
| Svarbūs faktai apie daugiakampius | |
|---|---|
| Daugiakampio vidinių kampų suma | (n–2) × 180° |
| Įstrižainių skaičius daugiakampyje | n(n–3)/2 |
| Taisyklingo daugiakampio vidinis kampas | {(n–2) × 180°}/n |
| Taisyklingo daugiakampio išorinis kampas | 360°/n |
Turinys
- Kas yra daugiakampiai?
- Daugiakampio diagrama, pagrįsta kraštų skaičiumi
- Daugiakampių savybės
- Daugiakampio formos
- Daugiakampių tipai
- Daugiakampių formulės
- Kampai daugiakampiuose
- DUK
Kas yra daugiakampiai?
Terminas „daugiakampis“ kilęs iš graikų kalbos žodžio „polugonos“, kur „poli“ reiškia „daug“, o „gon“ reiškia „kampą“. linijos. Norint sudaryti uždarą formą, reikia mažiausiai trijų linijų segmentų. Jis paprastai žinomas kaip trikampis arba 3 kampų. Bendras n-pusio daugiakampio terminas yra n-kampis.
Daugiakampio apibrėžimas
Daugiakampiai yra plokščios dvimatės figūros, sudarytos iš tiesių kraštų, kurios sudaro visiškai uždarą formą. Geometrijoje daugiakampis yra plokštumos figūra, sudaryta iš linijos atkarpų, sujungtų taip, kad sudarytų uždarą daugiakampę grandinę. Jie susideda iš tiesių kraštų, o ne išlenktų, ir gali turėti skirtingą šonų skaičių. Kai kurie įvairių tipų daugiakampiai yra atviri, tik ribiniai, uždari ir susikertantys.
Geometrijoje daugiakampis apibrėžiamas kaip uždara, dvimatė forma, kuri yra plokščia plokštumoje ir yra aptverta tiesiomis kraštinėmis.
rj12 prieš rj11
Daugiakampis neturi išlenktų kraštų, o jo kraštai yra tiesūs segmentai, apibrėžiantys jo ribą. Šių briaunų susitikimo taškai vadinami viršūnėmis arba kampais.
Daugiakampių pavyzdžiai
Matematikos požiūriu, daugiakampių pavyzdžiai yra šešiakampiai, penkiakampiai ir keturkampiai. Realūs daugiakampio pavyzdžiai yra stačiakampio formos ekranas nešiojamajame kompiuteryje, televizoriuje, mobiliajame telefone; stačiakampė futbolo aikštė arba žaidimų aikštelė, Bermudų trikampis ir trikampio formos Egipto piramidės.

Daugiakampio dalys
Daugiakampį sudaro trys pagrindiniai komponentai:
- Daugiakampio kraštinės: Daugiakampių kraštinės yra daugiakampių, apibrėžiančių uždarą sritį, ribos.
- Viršūnės: Taškas, kuriame susitinka dvi pusės, yra žinomas kaip viršūnė.
- Kampai: Daugiakampyje yra tiek vidinių, tiek išorinių kampų. Vidinis kampas susidaro uždaroje daugiakampio srityje, susikirtus jo kraštinėms.
Daugiakampio diagrama, pagrįsta kraštų skaičiumi
Daugiakampio nomenklatūra, apibrėžta pagal jų turimų kraštinių skaičių. Jis žymimas n-kampiais, kur „n“ reiškia kraštų skaičių. Daugiakampiai paprastai identifikuojami pagal jų kraštų skaičių. Pavyzdžiui, daugiakampis su penkiomis kraštinėmis vadinamas 5 kampu, o vienas su dešimt kraštinių vadinamas 10 kampu.
| Daugiakampio diagrama | ||||
|---|---|---|---|---|
| Daugiakampių formų pavadinimai | Šonų skaičius | Viršūnių skaičius | Įstrižainių skaičius | Vidaus kampo matas taisyklingai formai |
| Trikampis | Daugiakampiai su 3 kraštinėmis | 3 | 0 | 60° |
| Keturkampis | Daugiakampiai su 4 kraštinėmis | 4 | 2 | 90° |
| Pentagonas | Daugiakampiai su 5 kraštinėmis | 5 | 5 | 108° |
| Šešiakampis | Daugiakampiai su 6 kraštinėmis | 6 | 9 | 120° |
| Septynikampis | Daugiakampiai su 7 kraštinėmis | 7 | 14 | 128,571° |
| Aštuonkampis | Daugiakampiai su 8 kraštinėmis | 8 | dvidešimt | 135° |
| Nonagonas | Daugiakampiai su 9 kraštinėmis | 9 | 27 | 140° |
| Dešimtkampis | Daugiakampiai su 10 kraštinių | 10 rekha indėnė | 35 | 144° |
| Hendecagon | Daugiakampiai su 11 kraštinių | vienuolika | 44 | 147,273° |
| Dodecagon | Daugiakampiai su 12 kraštinių | 12 | 54 | 150° |
Daugiakampių savybės
Daugiakampių savybės juos lengvai atpažįsta. Šios savybės padeda lengvai pažinti daugiakampius:
- Daugiakampis yra uždara forma, neturinti atvirų galų. Kilmės ir pabaigos taškai turi būti vienodi.
- Jis įgauna plokštuminę formą, sudarytą iš linijų atkarpų arba tiesių linijų, kurios kartu formuoja figūrą.
- Kaip dvimatis subjektas, daugiakampis egzistuoja tik ilgio ir pločio matmenimis, jam trūksta gylio ar aukščio.
- Jis turi tris ar daugiau kraštinių, kad sudarytų daugiakampį.
- Daugiakampio kampai gali skirtis. Tai rodo skirtingą konfigūraciją.
- Daugiakampio kraštinių ilgis gali skirtis; jis gali būti vienodas visame daugiakampyje arba ne.
Daugiakampio formos
Daugiakampis yra plokščia, dvimatė forma, kuriai būdingos tiesios kraštinės, sujungtos į uždarą figūrą. Daugiakampių formų pavyzdžiai:
- Trikampis
- Keturkampis
- Pentagonas
- Šešiakampis
- Septynikampis
- Aštuonkampis
- Nonagonas
- Dešimtkampis
Trikampis
- Jis turi 3 kraštus ir 3 viršūnes.
- Jame nėra įstrižainių.
- Vidaus suma 180°.
Keturkampis
- Jis turi 4 kraštus ir 4 viršūnes.
- Jame yra 2 įstrižainės.
- Vidinio kampo suma yra 360°.
Pentagonas
- Jis turi 5 puses ir 5 viršūnes.
- Jame yra 5 įstrižainės.
- Vidinio kampo suma yra 540°.
Šešiakampis
- Jis turi 6 puses ir 6 viršūnes.
- Jame yra 9 įstrižainės.
- Vidinio kampo suma yra 720°.
Septynikampis
- Jis turi 7 puses ir 7 viršūnes.
- Jis turi 14 įstrižainių.
- Vidinio kampo suma yra 900°.
Aštuonkampis
- Jis turi 8 puses ir 8 viršūnes.
- Jis turi 20 įstrižainių.
- Vidinio kampo suma yra 1080°.
Nonagonas
- Jis turi 9 puses ir 9 viršūnes.
- Jame yra 27 įstrižainės.
- Vidinio kampo suma yra 1260°.
Dešimtkampis
- Jis turi 10 kraštinių ir 10 viršūnių.
- Jame yra 35 įstrižainės.
- Vidinio kampo suma yra 1440°.
Daugiakampių tipai
Priklausomai nuo kraštinių ir kampų, daugiakampiai gali būti skirstomi į skirtingus tipus skirtingais pagrindais, pavyzdžiui:
- Šonų pagrindu
- Kampų pagrindu
- Remiantis riba
Daugiakampiai kraštinių pagrindu
Daugiakampiai gali būti suskirstyti į du pagrindinius tipus, atsižvelgiant į jų kraštinių ypatybes:
- Taisyklingas daugiakampis
- Netaisyklingas daugiakampis
Taisyklingas daugiakampis
Taisyklingasis daugiakampis išsiskiria tuo, kad jo visos kraštinės yra vienodo ilgio ir visi vidiniai kampai vienodo dydžio. Jis gali būti ir lygiakraštis, ir lygiakampis. Taisyklingų daugiakampių pavyzdžiai yra trikampis, keturkampis, penkiakampis ir šešiakampis.

Taisyklingas daugiakampis
Netaisyklingas daugiakampis
Netaisyklingas daugiakampis turi nevienodo ilgio kraštines ir skirtingų matmenų kampus. Bet koks daugiakampis, kuris neatitinka taisyklingo daugiakampio kriterijų, yra klasifikuojamas kaip netaisyklingas. Dažni netaisyklingo daugiakampio pavyzdžiai yra mastelinis trikampis, keturkampiai, tokie kaip stačiakampis, trapecija arba aitvaras, taip pat netaisyklingos penkiakampės ir šešiakampės struktūros.
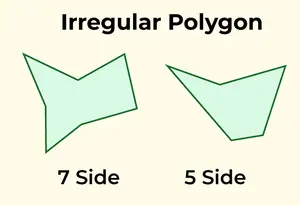
Netaisyklingas daugiakampis
Daugiakampiai kampų pagrindu
Daugiakampiai gali būti suskirstyti į dvi pagrindines kategorijas, atsižvelgiant į jų kampų pobūdį:
- Išgaubtas daugiakampis
- Įgaubtas daugiakampis
Išgaubtas daugiakampis
Išgaubtas daugiakampis neturi vidinio kampo, kuris būtų didesnis nei 180°. Išgaubti daugiakampiai gali turėti tris ar daugiau kraštinių. Išgaubtuose daugiakampiuose visos įstrižainės yra uždaros figūros viduje. Įprasti išgaubtų daugiakampių pavyzdžiai yra trikampiai, visi išgaubti keturkampiai, taip pat taisyklingi penkiakampiai ir šešiakampiai
Įgaubtas daugiakampis
Įgaubtas daugiakampis turi bent vieną vidinį kampą, kuris yra refleksinis kampas ir nukreiptas į vidų. Įgaubti daugiakampiai turi mažiausiai keturias kraštines. Šio tipo daugiakampyje yra bent vienas vidinis kampas, didesnis nei 180°. Įgaubtuose daugiakampiuose kai kurios įstrižainės tęsiasi už uždaros figūros ribų. Įgaubtų daugiakampių pavyzdžiai yra smiginis arba strėlės antgalis keturkampiuose, taip pat tam tikri netaisyklingi penkiakampiai ir šešiakampiai.
Skirtumas tarp įgaubtų ir išgaubtų daugiakampių
Pažiūrėkime, kuo skiriasi išgaubtas ir įgaubtas daugiakampis toliau pateiktoje lentelėje:

| Išgaubtas daugiakampis | Įgaubtas daugiakampis |
|---|---|
| Visas išgaubtos formos perimetras tęsiasi į išorę be jokių įdubimų į vidų. | Įgaubta forma turi bent vieną į vidų nukreiptą dalį, rodančią, kad yra įdubimas. |
| Išgaubtame daugiakampyje visi vidiniai kampai yra mažesni nei 180°. | Įgaubtame daugiakampyje yra bent vienas vidinis kampas, viršijantis 180°. |
| Bet kuri linija, jungianti dvi išgaubtos formos viršūnes, yra visiškai formos ribose. | Linija, jungianti bet kurias dvi įgaubtos formos viršūnes, gali arba negali kirsti formos vidų. |
Daugiakampiai ribų pagrindu
Daugiakampiai gali būti suskirstyti į du pagrindinius tipus, atsižvelgiant į jų ribų pobūdį:
- Paprastas daugiakampis
- Sudėtingas daugiakampis
Paprastas daugiakampis
Paprastam daugiakampiui būdinga vienaskaita, nesikertanti riba. Kitaip tariant, jis neperžengia savęs ir susideda iš vienos ribos.
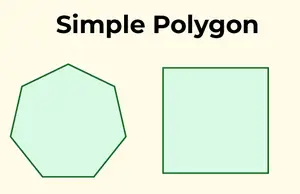
Paprasti daugiakampiai
Sudėtingas daugiakampis
Kita vertus, sudėtingą daugiakampį apibrėžia pats susikirtimas. Jį sudaro daugiau nei viena jo struktūra riba. Sudėtinguose daugiakampiuose ribos susikerta, sukurdamos kelias atskiras sritis daugiakampyje.

Sudėtingas daugiakampis
Skaityti Daugiau apie Daugiakampių tipai.
Daugiakampių formulės
Geometrijoje yra keletas formulių, susijusių su daugiakampiais. Kai kurie iš dažniausiai naudojamų yra:
- Ploto formulė
- Perimetro formulė
- Įstrižainių skaičius
Visos formulės, susijusios su skirtingais daugiakampiais, yra aptariamos toliau:
Daugiakampių plotas
Daugiakampio plotas reiškia bendrą erdvę, kurią jis užima dvimatėje plokštumoje, yra nustatomas pagal specialias formules, pagrįstas kraštinių skaičiumi ir daugiakampio klasifikacija. Ploto formulės yra tokios:
| Daugiakampio plotas | Formulė |
|---|---|
| Trikampio plotas | 1/2 × Pagrindas × Aukštis |
| Lygiagretaus plotas | Pagrindas × Aukštis |
| Stačiakampio plotas | Ilgis × Plotis |
| Aikštės plotas | (Šone)2 |
| 1/2 × įstrižainė1× įstrižainė2 | |
| Trapecijos sritis | 1/2 × aukštis × lygiagrečių kraštinių suma |
| (5/2) × kraštinės ilgis × Apothem | |
| Šešiakampio plotas | {(3√3)/2}pusę2 |
| Septynikampio sritis | 3,643 × šonas2 |
Daugiakampių perimetras
Dvimatės formos perimetras reiškia bendrą jos išorinės ribos ilgį. Daugiakampių perimetras apskaičiuojamas taip:
| Daugiakampio perimetras | Formulė |
|---|---|
| Trikampio perimetras | Trijų pusių suma |
| Lygiagretės perimetras | 2 (gretimų kraštinių suma) |
| Stačiakampio perimetras | 2 (ilgis + plotis) |
| Aikštės perimetras | 4 × šonas |
| Rombo perimetras | 4 × šonas |
| Trapecijos perimetras | Lygiagrečių kraštinių suma + Nelygiagrečių kraštinių suma |
| Pentagono perimetras | 5 × šonas |
| Šešiakampio perimetras | 6 × šonas |
| Septynikampio perimetras | 7 × šonas Kaip atsisiųsti video iš youtube vlc |
Daugiakampio formulės įstrižainė
Daugiakampio įstrižainė yra atkarpa, sudaryta sujungiant dvi negreta esančias viršūnes.
Įstrižainių skaičius daugiakampyje = n(n-3)/2,
Kur „n“ reiškia daugiakampio kraštinių skaičių.
Skaityti Daugiau apie Daugiakampio formulės įstrižainė .
Kampai daugiakampiuose
Geometrijoje daugiakampių kampai reiškia kampus, kuriuos sudaro daugiakampio kraštinės tiek daugiakampio viduje, tiek išorėje. Taigi, daugiakampyje gali būti abu kampai, t.y.
- Vidiniai kampai
- Išoriniai kampai
Išsamiai aptarkime šių kampų formulę taip:
Daugiakampių vidinė kampo formulė
Daugiakampio vidiniai kampai yra tie, kurie susidaro tarp gretimų jo kraštinių ir yra lygūs taisyklingo daugiakampio atveju. Vidinių kampų skaičius atitinka daugiakampio kraštinių skaičių.
Vidinių kampų „S“ suma daugiakampyje su „n“ kraštinėmis apskaičiuojama kaip
S = (n – 2) × 180°
Kur „n“ reiškia kraštų skaičių.
Daugiakampių išorinio kampo formulė
Kiekvienas taisyklingo daugiakampio išorinis kampas suformuojamas pratęsiant vieną iš jo kraštų (pagal laikrodžio rodyklę arba prieš laikrodžio rodyklę) ir išmatuojant kampą tarp šio išplėtimo ir gretimos kraštinės. Taisyklingo daugiakampio visi išoriniai kampai yra lygūs
Bendra bet kurio daugiakampio išorinių kampų suma yra 360°
Todėl,
Kiekvienas išorinis kampas nurodomas 360°/n
Kur „n“ yra pusių skaičius.
Vidinių ir atitinkamų išorinių kampų suma bet kurioje daugiakampio viršūnėje visada yra 180 laipsnių, išreiškiant papildomą ryšį:
Vidinis kampas + Išorinis kampas = 180°
Išorinis kampas = 180° – Vidinis kampas
Išvada
- Daugiakampis yra uždara figūra, kurią riboja trys ar daugiau linijos atkarpų
- Vidinių kampų suma: Visų vidinių kampų suma n kraštiniame daugiakampyje apskaičiuojama pagal formulę (n–2) × 180°.
- Įstrižainių skaičius: Daugiakampio su n kraštinėmis įstrižainių skaičius apskaičiuojamas pagal formulę n(n–3)/2.
- Trikampiai, sudaryti iš įstrižainių: Trikampių, susidarančių sujungus įstrižas iš vieno daugiakampio kampo, skaičius yra n–2.
- Vidinis reguliaraus daugiakampio kampas: Kiekvieno vidinio kampo matas n kraštų taisyklingame daugiakampyje yra {(n–2) × 180°}/n.
- Išorinis reguliaraus daugiakampio kampas: Kiekvieno išorinio kampo matas n kraštų taisyklingame daugiakampyje yra 360°/n.
Taip pat Skaitykite
- Kvadratas
- Lygiagretainis
- Stačiakampis
Išspręsti matematikos daugiakampio pavyzdžiai
1 pavyzdys: Apsvarstykite keturkampį su keturiomis kraštinėmis. Raskite visų jo vidinių keturkampio kampų sumą.
Sprendimas:
Vidinių kampų sumos formulė n pusių taisyklingame daugiakampyje = (n − 2) × 180°
Visų vidinių keturkampio kampų suma = (4 – 2) × 180°
Visų vidinių keturkampio kampų suma = 2 × 180°
Visų vidinių keturkampio kampų suma = 360°
Todėl visų keturkampio vidinių kampų suma yra 360°.
2 pavyzdys: Apsvarstykite reguliarųjį daugiakampį, kurio išorinio ir vidinio kampų santykis yra 7:3. Nustatykite daugiakampio tipą.
Sprendimas:
Išorinio ir vidinio kampo santykis yra 7:3.
Tarkime, kad daugiakampio išorinis ir vidinis kampas yra 7x ir 3x.
Bet kurio daugiakampio išorinių ir vidinių kampų suma yra 180°.
7x + 3x = 180°
10x = 180°
x = 18°
Išorinis kampas = 18°
Šonų skaičius = 360°/išorinis kampas
= 360°/18°
= 20
Todėl pateiktas daugiakampis yra ikosagonas, nes jis turi 20 kraštinių.
3 pavyzdys: kiekvienas daugiakampio išorinis kampas yra 90 laipsnių, nustatykite daugiakampio tipą?
Sprendimas:
Pagal formulę kiekvienas išorinis kampas = 360°/n
Čia n = pusių skaičius.
90°= 360°/n
n = 360°/90° = 4
Taigi aptariamas daugiakampis yra keturkampis, nes jis turi keturias puses.
4 pavyzdys: bortai yra 10 m, 10 m, 8 m, 8 m, 5 m, 5 m, 9 m, 9 m. Kiek metrų lyno reikės Perimetrui?
Sprendimas:
Norėdami rasti perimetrui reikalingą virvės ilgį, turime susumuoti visų kraštinių ilgius:
Perimetras = 10 m + 10 m + 8 m + 8 m + 5 m + 5 m + 9 m + 9 m
Perimetras = 64 m.
Todėl Perimetrui iš viso reikės 64 metrų virvės.
Praktikos klausimai apie daugiakampius geometrijoje
Toliau pateikiami keli praktiniai klausimai, pagrįsti daugiakampių formule:
Q1. Jei vienas penkiakampio kampas yra 140°, nustatykite didžiausio kampo dydį, jei likę kampai yra santykiu 1:2:3:4.
Q2. Jei daugiakampio vidinių kampų suma yra 160°, raskite daugiakampio kraštinių skaičių.
np.kur
Q3. Dviejų taisyklingų daugiakampių kraštinių skaičius yra 2:3, o jų vidinių kampų santykis yra 4:5. Raskite atitinkamą šių daugiakampių kraštinių skaičių.
4 klausimas. Nustatykite bendrą septyniakampio kampų sumą.
Q5. Apskaičiuokite penkiakampio išorinių kampų sumą.
6 klausimas. Kiek kraštinių turi šešiakampis?
- 4
- 6
- 8
- 10
7 klausimas. Kuris iš šių nėra taisyklingas daugiakampis?
- Trikampis
- Kvadratas
- Pentagonas
- Lygiagretainis
DUK apie daugiakampius matematikoje
Kas yra daugiakampis matematikoje?
Matematikoje daugiakampis reiškia uždarą dvimatę figūrą, suformuotą sujungus tris ar daugiau tiesių. Terminas „daugiakampis“ yra kilęs iš graikų kalbos, kuriame daug reiškia daug, o gon – kampą.
Kuris yra mažiausias daugiakampis?
Mažiausias suformuotas daugiakampis yra trikampis su trimis kraštinėmis.
Kas yra 20-gon?
20 kampų geometrijoje yra dvidešimties kraštų daugiakampis.
Kokia yra bendra daugiakampio išorinių kampų suma?
Daugiakampio išorinių kampų suma yra 360°.
Ar apskritimas gali būti klasifikuojamas kaip daugiakampis?
Daugiakampis yra uždara forma, sudaryta iš tiesių atkarpų. Apskritimas yra uždara figūra, bet ji sudaryta iš kreivės. Taigi apskritimas nėra daugiakampis.
Kokia yra daugiakampio vidinio kampo suma?
Daugiakampio vidinio kampo suma yra (n–2) × 180°, kur n yra daugiakampio kraštinių skaičius.
