Atsižvelgiant į dvi eilutes, S1 ir S2 , užduotis yra rasti ilgiausios bendrosios posekos ilgį, t. y. ilgiausią abiejose eilutėse esančią poseką.

A ilgiausia bendra seka (LCS) apibrėžiamas kaip ilgiausia poseka, kuri yra bendra visose nurodytose įvesties sekose.

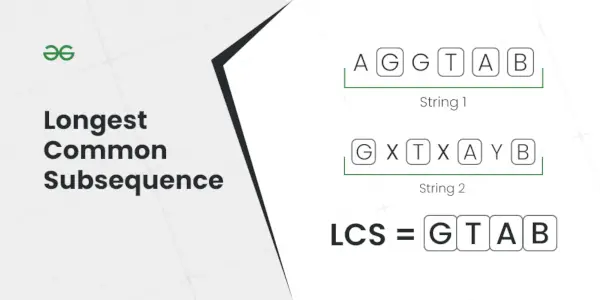
Ilgiausia bendra seka

java matematikos pow

Pavyzdžiai:

Įvestis: S1 = ABC, S2 = ACD
Išvestis: 2
Paaiškinimas: Ilgiausia poseka, esanti abiejose eilutėse, yra AC.

Įvestis: S1 = AGGTAB, S2 = GXTXAYB
Išvestis: 4
Paaiškinimas: Ilgiausia bendra seka yra GTAB.

Įvestis: S1 = ABC, S2 = CBA
Išvestis: 1
Paaiškinimas: Yra trys bendros posekos, kurių ilgis yra 1, A, B ir C, ir nėra bendros posekos, kurių ilgis didesnis nei 1.

Įvestis: S1 = XYZW, S2 = XYWZ
Išvestis: 3
Paaiškinimas: Yra dvi bendros posekos, kurių ilgis yra 3 XYZ ir XYW, ir nėra bendros posekos. kurių ilgis didesnis nei 3.

Ilgiausia bendra seka (LCS), naudojant rekursiją:

Sugeneruokite visas galimas posekes ir raskite iš jų ilgiausią, kuri yra abiejose naudojant eilutes Norėdami įgyvendinti idėją, atlikite šiuos veiksmus:

• Sukurkite rekursinę funkciją [tarkim lcs() ].
• Patikrinkite ryšį tarp dar neapdorotų eilučių pirmųjų simbolių.
  • Priklausomai nuo santykio, iškvieskite kitą rekursinę funkciją, kaip minėta aukščiau.
• Kaip atsakymą pateikite gauto LCS ilgį.

Žemiau pateikiamas rekursinio metodo įgyvendinimas:

C++

// A Naive recursive implementation of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], Y[0..n-1] int lcs(string X, string Y, int m, int n)  // Driver code int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  int m = S1.size();  int n = S2.size();  cout << 'Length of LCS is ' << lcs(S1, S2, m, n);  return 0; } // This code is contributed by rathbhupendra>

C

// A Naive recursive implementation // of LCS problem #include  int max(int a, int b); // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int i, int j)  // Utility function to get max of // 2 integers int max(int a, int b) { return (a>b)? a : b; } // Tvarkyklės kodas int main() { char S1[] = 'BD';  char S2[] = 'ABCD';  int m = strlen(S1);  int n = strlen(S2);  int i = 0, j = 0;  // Funkcijos iškvietimas printf('LCS ilgis yra %d', lcs(S1, S2, i, j));  grąžinti 0; }>

Java

// A Naive recursive implementation of LCS problem in java import java.io.*; import java.util.*; public class LongestCommonSubsequence {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  int lcs(String X, String Y, int m, int n)   n == 0)  return 0;  if (X.charAt(m - 1) == Y.charAt(n - 1))  return 1 + lcs(X, Y, m - 1, n - 1);  else  return max(lcs(X, Y, m, n - 1),  lcs(X, Y, m - 1, n));    // Utility function to get max of 2 integers  int max(int a, int b) { return (a>b)? a : b; } // Tvarkyklės kodas public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence();  Eilutė S1 = 'AGGTAB';  Eilutė S2 = 'GXTXAYB';  int m = S1.ilgis();  int n = S2.ilgis();  System.out.println('LCS ilgis yra' + ' ' + lcs.lcs(S1, S2, m, n));  } } // Šį kodą sukūrė Saket Kumar>>Python

C#

// C# Naive recursive implementation of LCS problem using System; class GFG {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n)    if (m == 0   // Utility function to get max of 2 integers  static int max(int a, int b) { return (a>b)? a : b; } // Tvarkyklės kodas public static void Main() { String S1 = 'AGGTAB';  Eilutė S2 = 'GXTXAYB';  int m = S1.Ilgis;  int n = S2.Ilgis;  Console.Write('LCS ilgis yra' + ' ' + lcs(S1, S2, m, n));  } } // Šį kodą sukūrė Sam007>>Javascript>>PHP>>  
  Išvestis  
Length of LCS is 4>
  
    Laiko sudėtingumas:    O(2m+n)  
    Pagalbinė erdvė:    O(1)
 
Naudojant ilgiausią bendrąją seką (LCS).  Atmintinė : 
 Jei atidžiai pastebėsime, galime pastebėti, kad aukščiau pateiktas rekursyvus sprendimas turi šias dvi savybes: 
  
1. Optimali pagrindo struktūra:
Norėdami išspręsti L(X[0, 1, . . ., m-1], Y[0, 1, . . . , n-1]) struktūrą, žr. X[0 , 1, …, m-2], Y[0, 1,…, n-2], priklausomai nuo situacijos (t.y. naudojant juos optimaliai) rasti visumos sprendimą.
 
2. Sutampančios poproblemos:
Jei eilutėms naudosime aukščiau pateiktą rekursinį metodą    BD    ir    ABCD    , gausime dalinį rekursijos medį, kaip parodyta žemiau. Čia matome, kad poproblema L(BD, ABCD) skaičiuojama ne vieną kartą. Jei atsižvelgsime į bendrą medį, bus keletas tokių sutampančių subproblemų.
  
L (AXYT, AYZX)  
/  
L (AXY, AYZX) L (AXYT, AYZ)  
/  /   
L (AX, AYZX) L (AXY, AYZ) L (AXY, AYZ) L (AXYT, AY)
 
    Metodas:    Dėl šių dviejų savybių problemai išspręsti galime naudoti dinaminį programavimą arba atmintinę. Žemiau pateikiamas sprendimo metodas naudojant rekursiją.
  
Sukurkite rekursinę funkciją. Taip pat sukurkite 2D masyvą, kad išsaugotumėte unikalios būsenos rezultatą.
Rekursinio skambučio metu, jei ta pati būsena iškviečiama daugiau nei vieną kartą, galime tiesiogiai grąžinti tos būsenos išsaugotą atsakymą, o ne skaičiuoti iš naujo.
Žemiau pateikiamas pirmiau minėto metodo įgyvendinimas:
C++ 
// A Top-Down DP implementation // of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int m, int n,  vector>& dp) { if (m == 0 || n == 0) return 0;  jei (X[m - 1] == Y[n - 1]) grąžinti dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  if (dp[m][n] != -1) { return dp[m][n];  } return dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)); } // Tvarkyklės kodas int main() { char X[] = 'AGGTAB';  char Y[] = 'GXTXAYB';  int m = strlen(X);  int n = strlen(Y);  vektorius> dp(m + 1, vektorius (n + 1, -1));  cout<< 'Length of LCS is ' << lcs(X, Y, m, n, dp);  return 0; }>
 Java 
/*package whatever //do not write package name here */ import java.io.*; class GFG {  // A Top-Down DP implementation of LCS problem  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n,  int[][] dp)  {  if (m == 0 || n == 0)  return 0;  if (dp[m][n] != -1)  return dp[m][n];  if (X.charAt(m - 1) == Y.charAt(n - 1)) {  dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  return dp[m][n];  }  dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp),  lcs(X, Y, m - 1, n, dp));  return dp[m][n];  }  // Drivers code  public static void main(String args[])  {  String X = 'AGGTAB';  String Y = 'GXTXAYB';  int m = X.length();  int n = Y.length();  int[][] dp = new int[m + 1][n + 1];  for (int i = 0; i < m + 1; i++) {  for (int j = 0; j < n + 1; j++) {  dp[i][j] = -1;  }  }  System.out.println('Length of LCS is '  + lcs(X, Y, m, n, dp));  } } // This code is contributed by shinjanpatra>
 Python 
# A Top-Down DP implementation of LCS problem # Returns length of LCS for X[0..m-1], Y[0..n-1] def lcs(X, Y, m, n, dp): if (m == 0 or n == 0): return 0 if (dp[m][n] != -1): return dp[m][n] if X[m - 1] == Y[n - 1]: dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp) return dp[m][n] dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)) return dp[m][n] # Driver code X = 'AGGTAB' Y = 'GXTXAYB' m = len(X) n = len(Y) dp = [[-1 for i in range(n + 1)]for j in range(m + 1)] print(f'Length of LCS is {lcs(X, Y, m, n, dp)}') # This code is contributed by shinjanpatra>
 C# 
/* C# Naive recursive implementation of LCS problem */ using System; class GFG {  /* Returns length of LCS for X[0..m-1], Y[0..n-1] */  static int lcs(char[] X, char[] Y, int m, int n,  int[, ] L)  {  if (m == 0 || n == 0)  return 0;  if (L[m, n] != -1)  return L[m, n];  if (X[m - 1] == Y[n - 1]) {  L[m, n] = 1 + lcs(X, Y, m - 1, n - 1, L);  return L[m, n];  }  L[m, n] = max(lcs(X, Y, m, n - 1, L),  lcs(X, Y, m - 1, n, L));  return L[m, n];  }  /* Utility function to get max of 2 integers */  static int max(int a, int b) { return (a>b)? a : b; } public static void Main() { String s1 = 'AGGTAB';  Eilutė s2 = 'GXTXAYB';  char[] X = s1.ToCharArray();  char[] Y = s2.ToCharArray();  int m = X. Ilgis;  int n = Y. Ilgis;  int[, ] L = naujas int[m + 1, n + 1];  už (int i = 0; i<= m; i++) {  for (int j = 0; j <= n; j++) {  L[i, j] = -1;  }  }  Console.Write('Length of LCS is'  + ' ' + lcs(X, Y, m, n, L));  } } // This code is contributed by akshitsaxenaa09>
 Javascript 
/* A Top-Down DP implementation of LCS problem */ /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ function lcs(X, Y, m, n, dp) {  if (m == 0 || n == 0)  return 0;  if (X[m - 1] == Y[n - 1])  return dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  if (dp[m][n] != -1) {  return dp[m][n];  }  return dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp),  lcs(X, Y, m - 1, n, dp)); } /* Driver code */ let X = 'AGGTAB'; let Y = 'GXTXAYB'; let m = X.length; let n = Y.length; let dp = new Array(m + 1); for(let i = 0; i < m + 1; i++) {  dp[i] = new Array(n + 1).fill(-1); }  console.log('Length of LCS is ' + lcs(X, Y, m, n, dp)); // This code is contributed by shinjanpatra>
   
  Išvestis      Laiko sudėtingumas:    O(m * n), kur m ir n yra eilutės ilgiai.  
    Pagalbinė erdvė:    O(m * n) Čia nepaisoma rekursyvios dėklo erdvės.
 
Ilgiausia bendra seka (LCS) naudojant „Iš apačios į viršų“ (lentelių):
Galime naudoti šiuos veiksmus, kad įgyvendintume LCS dinaminio programavimo metodą.
 
Sukurkite 2D masyvą    dp[][]    kurių eilutės ir stulpeliai lygūs kiekvienos įvesties eilutės ilgiui plius 1 [eilučių skaičius rodo indeksus    S1    o stulpeliuose nurodomi indeksai    S2    ].
Pirmąją dp masyvo eilutę ir stulpelį inicijuokite į 0.
Pakartokite per dp masyvo eilutes, pradedant nuo 1 (tarkime naudodami iteratorių    i    ).
Kiekvienam    i    , kartokite visus stulpelius iš    j = 1 iki n    :
Jeigu    S1[i-1]    yra lygus    S2[j-1]    , nustatykite dabartinį dp masyvo elementą į elemento vertę į (    dp[i-1][j-1] + 1    ).
Kitu atveju nustatykite dabartinį dp masyvo elementą į didžiausią reikšmę    dp[i-1][j]    ir    dp[i][j-1]    .
Po įdėtųjų kilpų paskutiniame dp masyvo elemente bus nurodytas LCS ilgis.
Norėdami geriau suprasti, žiūrėkite toliau pateiktą iliustraciją:
 
    Iliustracija:    
  
Tarkime, kad stygos yra    S1 = AGGTAB    ir    S2 = GXTXAYB    .
Java duomenų tipai
 
    Pirmas žingsnis:    Iš pradžių sukurkite 8 x 7 dydžio 2D matricą (tarkim dp[][]), kurios pirmoji eilutė ir pirmas stulpelis užpildyti 0.
  
Dp lentelės kūrimas
    Antras žingsnis:    Traversas, kai i = 1. Kai j tampa 5, S1[0] ir S2[4] yra lygūs. Taigi dp[][] atnaujintas. Kitų elementų didžiausias dydis yra dp[i-1][j] ir dp[i][j-1]. (Šiuo atveju, jei abi reikšmės yra lygios, mes naudojome rodykles į ankstesnes eilutes).
  
1 eilutės užpildymas
    Trečias žingsnis:    S1[1] ir S2[0] yra vienodi (abu yra G). Taigi dp reikšmė tame langelyje atnaujinama. Likę elementai atnaujinami pagal sąlygas.
  
Užpildant eilutę Nr. 2
    Ketvirtas žingsnis:    Jei i = 3, S1[2] ir S2[0] vėl yra vienodi. Atnaujinimai yra tokie.
  
Užpildykite eilutę Nr. 3
    Penktas žingsnis:    Jei i = 4, matome, kad S1[3] ir S2[2] yra vienodi. Taigi dp[4][3] atnaujintas kaip dp[3][2] + 1 = 2.
  
4 eilutės užpildymas
    Šeštas žingsnis:    Čia matome, kad i = 5 ir j = 5 S1[4] ir S2[4] reikšmės yra vienodos (t. y. abi yra „A“). Taigi dp[5][5] atitinkamai atnaujinamas ir tampa 3.
  
5 eilutės užpildymas
    Paskutinis žingsnis:    Jei i = 6, žiūrėkite, kad paskutiniai abiejų eilučių simboliai yra vienodi (jie yra „B“). Todėl dp[6][7] reikšmė tampa 4.
  
Paskutinės eilutės užpildymas
Taigi gauname didžiausią bendros posekos ilgį kaip    4    .
 
Toliau pateikiamas LCS problemos įgyvendinimas lentelėje.
C++ 
// Dynamic Programming C++ implementation // of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(string X, string Y, int m, int n) {  // Initializing a matrix of size  // (m+1)*(n+1)  int L[m + 1][n + 1];  // Following steps build L[m+1][n+1]  // in bottom up fashion. Note that  // L[i][j] contains length of LCS of  // X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)   if (i == 0   }  // L[m][n] contains length of LCS  // for X[0..n-1] and Y[0..m-1]  return L[m][n]; } // Driver code int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  int m = S1.size();  int n = S2.size();  // Function call  cout << 'Length of LCS is ' << lcs(S1, S2, m, n);  return 0; }>
 Java 
// Dynamic Programming Java implementation of LCS problem import java.util.*; public class LongestCommonSubsequence {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  int lcs(String X, String Y, int m, int n)  {  int L[][] = new int[m + 1][n + 1];  // Following steps build L[m+1][n+1] in bottom up  // fashion. Note that L[i][j] contains length of LCS  // of X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)  j == 0)  L[i][j] = 0;  else if (X.charAt(i - 1) == Y.charAt(j - 1))  L[i][j] = L[i - 1][j - 1] + 1;  else  L[i][j] = max(L[i - 1][j], L[i][j - 1]);    }  return L[m][n];  }  // Utility function to get max of 2 integers  int max(int a, int b) { return (a>b)? a : b; } public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence();  Eilutė S1 = 'AGGTAB';  Eilutė S2 = 'GXTXAYB';  int m = S1.ilgis();  int n = S2.ilgis();  System.out.println('LCS ilgis yra' + ' ' + lcs.lcs(S1, S2, m, n));  } } // Šį kodą sukūrė Saket Kumar>>Python
 C# 
// Dynamic Programming implementation of LCS problem using System; class GFG {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n)  {  int[, ] L = new int[m + 1, n + 1];  // Following steps build L[m+1][n+1]  // in bottom up fashion.  // Note that L[i][j] contains length of  // LCS of X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)  j == 0)  L[i, j] = 0;  else if (X[i - 1] == Y[j - 1])  L[i, j] = L[i - 1, j - 1] + 1;  else  L[i, j] = max(L[i - 1, j], L[i, j - 1]);    }  return L[m, n];  }  // Utility function to get max of 2 integers  static int max(int a, int b) { return (a>b)? a : b; } // Tvarkyklės kodas public static void Main() { String S1 = 'AGGTAB';  Eilutė S2 = 'GXTXAYB';  int m = S1.Ilgis;  int n = S2.Ilgis;  Console.Write('LCS ilgis yra' + ' ' + lcs(S1, S2, m, n));  } } // Šį kodą sukūrė Sam007>>Javascript
 PHP 
 // Dynamic Programming C#  // implementation of LCS problem  function lcs($X , $Y, $m, $n) { // Following steps build L[m+1][n+1]  // in bottom up fashion .  // Note: L[i][j] contains length of  // LCS of X[0..i-1] and Y[0..j-1] for ($i = 0; $i <= $m; $i++) { for ($j = 0; $j <= $n; $j++)  if ($i == 0  } // L[m][n] contains the length of  // LCS of X[0..n-1] & Y[0..m-1]  return $L[$m][$n]; } // Driver Code  $S1 = 'AGGTAB'; $S2 = 'GXTXAYB'; $m = strlen($S1); $n = strlen($S2) ; echo 'Length of LCS is '; echo lcs($S1, $S2, $m, $n); // This code is contributed  // by Shivi_Aggarwal  ?>>>  
  Išvestis  
Length of LCS is 4>
  
    Laiko sudėtingumas:    O(m * n), kuris yra daug geresnis nei blogiausio atvejo naivaus rekursyvaus diegimo laiko sudėtingumas.  
    Pagalbinė erdvė:    O(m * n), nes algoritmas naudoja (m+1)*(n+1) dydžio masyvą bendrų eilučių ilgiui saugoti.
 
Ilgiausia bendra seka (LCS) naudojant „iš apačios į viršų“ (erdvės optimizavimą):
 
Taikant aukščiau pateiktą lentelių sudarymo metodą, mes naudojame L[i-1][j] ir L[i][j] ir tt, čia L[i-1] nurodo ankstesnę matricos L eilutę, o L[i] nurodo dabartinę eilutę.
Erdvę galime optimizuoti naudodami du vektorius, iš kurių vienas yra ankstesnis, o kitas yra dabartinis.
Kai vidinė for kilpa išeina, inicijuojame ankstesnį lygų srovei.
Žemiau pateikiamas įgyvendinimas:
C++ 
// Dynamic Programming C++ implementation // of LCS problem #include  using namespace std; int longestCommonSubsequence(string& text1, string& text2) {  int n = text1.size();  int m = text2.size();  // initializing 2 vectors of size m  vector ankstesnis(m + 1, 0), kur(m + 1, 0);  for (int idx2 = 0; idx2< m + 1; idx2++)  cur[idx2] = 0;  for (int idx1 = 1; idx1 < n + 1; idx1++) {  for (int idx2 = 1; idx2 < m + 1; idx2++) {  // if matching  if (text1[idx1 - 1] == text2[idx2 - 1])  cur[idx2] = 1 + prev[idx2 - 1];  // not matching  else  cur[idx2]  = 0 + max(cur[idx2 - 1], prev[idx2]);  }  prev = cur;  }  return cur[m]; } int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  // Function call  cout << 'Length of LCS is '  << longestCommonSubsequence(S1, S2);  return 0; }>
 Java 
// Dynamic Programming Java implementation of LCS problem import java.util.Arrays; public class GFG {  public static int longestCommonSubsequence(String text1, String text2) {  int n = text1.length();  int m = text2.length();  // Initializing 2 arrays of size m  int[] prev = new int[m + 1];  int[] cur = new int[m + 1];  for (int idx1 = 1; idx1 < n + 1; idx1++) {  for (int idx2 = 1; idx2 < m + 1; idx2++) {  // If matching  if (text1.charAt(idx1 - 1) == text2.charAt(idx2 - 1))  cur[idx2] = 1 + prev[idx2 - 1];  // Not matching  else  cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]);  }  prev = Arrays.copyOf(cur, m + 1);  }  return cur[m];  }  public static void main(String[] args) {  String S1 = 'AGGTAB';  String S2 = 'GXTXAYB';  // Function call  System.out.println('Length of LCS is ' + longestCommonSubsequence(S1, S2));  } }>
 Python 
def longestCommonSubsequence(text1, text2): n = len(text1) m = len(text2) # Initializing two lists of size m prev = [0] * (m + 1) cur = [0] * (m + 1) for idx1 in range(1, n + 1): for idx2 in range(1, m + 1): # If characters are matching if text1[idx1 - 1] == text2[idx2 - 1]: cur[idx2] = 1 + prev[idx2 - 1] else: # If characters are not matching cur[idx2] = max(cur[idx2 - 1], prev[idx2]) prev = cur.copy() return cur[m] if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' # Function call print('Length of LCS is', longestCommonSubsequence(S1, S2)) # This code is contributed by Rishabh Mathur>
 C# 
using System; class Program {  static int LongestCommonSubsequence(string text1, string text2)  {  int n = text1.Length;  int m = text2.Length;  // initializing 2 arrays of size m  int[] prev = new int[m + 1];  int[] cur = new int[m + 1];  for (int idx2 = 0; idx2 < m + 1; idx2++)  cur[idx2] = 0;  for (int idx1 = 1; idx1 < n + 1; idx1++)  {  for (int idx2 = 1; idx2 < m + 1; idx2++)  {  // if matching  if (text1[idx1 - 1] == text2[idx2 - 1])  cur[idx2] = 1 + prev[idx2 - 1];  // not matching  else  cur[idx2] = 0 + Math.Max(cur[idx2 - 1], prev[idx2]);  }  prev = cur;  }  return cur[m];  }  static void Main()  {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  // Function call  Console.WriteLine('Length of LCS is ' + LongestCommonSubsequence(S1, S2));  } }>
 Javascript 
function longestCommonSubsequence(text1, text2) {  const n = text1.length;  const m = text2.length;  // Initializing two arrays of size m  let prev = new Array(m + 1).fill(0);  let cur = new Array(m + 1).fill(0);  for (let idx2 = 0; idx2 < m + 1; idx2++) {  cur[idx2] = 0;  }  for (let idx1 = 1; idx1 < n + 1; idx1++) {  for (let idx2 = 1; idx2 < m + 1; idx2++) {  // If characters match  if (text1[idx1 - 1] === text2[idx2 - 1]) {  cur[idx2] = 1 + prev[idx2 - 1];  }  // If characters don't match  else {  cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]);  }  }  // Update the 'prev' array  prev = [...cur];  }  return cur[m]; } // Main function function main() {  const S1 = 'AGGTAB';  const S2 = 'GXTXAYB';  // Function call  console.log('Length of LCS is ' + longestCommonSubsequence(S1, S2)); } // Call the main function main();>
   
  Išvestis      Laiko sudėtingumas:    O(m * n), kuris išlieka toks pat.  
    Pagalbinė erdvė:    O(m), nes algoritmas naudoja du m dydžio matricas.