Terminas Atmintinė kilęs iš lotyniško žodžio memorandumą ( Prisiminti ), kuris amerikiečių anglų kalba paprastai sutrumpinamas į atmintinę ir reiškia funkcijos rezultatus paversti tuo, ką reikia atsiminti.
Skaičiuojant atmintinė naudojama norint pagreitinti kompiuterių programas, pašalinant pasikartojančius rezultatų skaičiavimus ir išvengiant pasikartojančių iškvietimų į funkcijas, kurios apdoroja tą pačią įvestį.

Kas yra atmintinė
Turinys
- Kas yra atmintis?
- Kodėl naudojama atmintinė>
- Kur naudoti atmintinę?
- Atmintinės rūšys
- Kaip memoization technika naudojama dinaminiame programavime?
- Kuo Memoization skiriasi nuo lentelių sudarymo?
- Atmintinės kodavimo praktikos problemos
- DUK
- 1) Ar atmintis yra geriau nei DP?
- 2) Ar įrašymas į atmintį yra tas pats, kas kaupimas talpykloje?
- 3) Kodėl atmintyje rašoma iš viršaus į apačią?
- 4) Ar atmintyje naudojama rekursija?
- 5) Ar turėčiau naudoti lentelę ar atmintinę?
- 6) Kur naudojama atmintis?
- 7) Kodėl tai vadinama atmintimi?
- 8) Kaip atmintinė sumažina laiko sudėtingumą?
- 9) Kuo skiriasi atmintinė ir talpyklos kaupimas?
- 10) Kodėl lentelės sudarymas yra greitesnis nei atmintinė?
- Išvada
Kodėl naudojama atmintinė?
Memoizacija yra specifinė forma talpykloje kuris naudojamas dinaminis programavimas . Talpyklos saugojimo tikslas – pagerinti mūsų programų našumą ir užtikrinti, kad duomenys būtų pasiekiami, kuriuos būtų galima panaudoti vėliau. Iš esmės jis išsaugo anksčiau apskaičiuotą antrinės problemos rezultatą ir naudoja išsaugotą rezultatą tai pačiai subproblemai. Tai pašalina papildomas pastangas vėl ir vėl skaičiuoti dėl tos pačios problemos. Ir mes jau žinome, kad jei ta pati problema kartojasi vėl ir vėl, tada ta problema yra pasikartojanti.
Kur naudoti atmintinę?
Galime naudoti atmintinės techniką, kai naudojant anksčiau apskaičiuotus rezultatus patenka į paveikslą. Tokio pobūdžio problema dažniausiai naudojama kontekste rekursija , ypač su susijusiomis problemomis persidengiančios subproblemos .
Paimkime pavyzdį, kai ta pati subproblema kartojasi vėl ir vėl.
Pavyzdys, rodantis, kur naudoti atmintinę:
Let us try to find the factorial of a number .>
Žemiau yra a rekursinis metodas Norėdami rasti skaičiaus faktorialą:
int faktorialas (nepasirašytas int n)
{
jei (n == 0)
grąžinti 1;
return n * faktorialas(n – 1);
}
Kas atsitiks, jei naudosime šį rekursinį metodą?
Jei parašysite visą aukščiau esančio fragmento kodą, pastebėsite, kad kode bus 2 būdai:
1. factorial(n) 2. main()>
Dabar, jei turime kelias užklausas, kad surastume faktorialą, pvz., 2, 3, 9 ir 5 faktorialą, tada faktorial() metodą turėsime iškviesti 4 kartus:
factorial(2) factorial(3) factorial(9) factorial(5)>
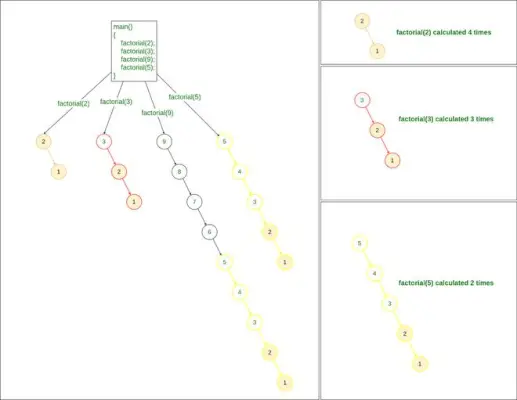
Rekursyvus faktoriaus nustatymo metodas
Taigi galima drąsiai teigti, kad norint rasti skaičių faktorių K skaičių, reikės laiko sudėtingumo O (N*K)
- O(N) rasti tam tikro skaičiaus faktorialą ir
- RODYKLĖ) faktorial() metodą K iškviesti skirtingais laikais.
Kaip atmintis gali padėti sprendžiant tokias problemas?
Jei pastebėsime aukščiau pateiktą problemą, skaičiuodami faktorių 9:
žemėlapiai java
- Skaičiuojame faktorialą iš 2
- Taip pat apskaičiuojame faktorialą 3,
- ir Mes taip pat skaičiuojame faktorialą iš 5
Todėl, jei išsaugosime kiekvieno atskiro faktorialo rezultatą pirmą kartą skaičiuodami, galime lengvai grąžinti bet kurio reikiamo skaičiaus faktorialą tik per O(1) laiką. Šis procesas žinomas kaip Atmintinė .
Sprendimas naudojant atmintinę (kaip veikia atmintinė?):
Jei pirmiausia rasime faktorialą iš 9 ir išsaugome atskirų antrinių uždavinių rezultatus, galime lengvai atspausdinti kiekvienos įvesties faktorialą O(1).
Todėl faktorinių skaičių paieška naudojant atmintinę bus sudėtinga O(N)
- O(N) rasti didžiausios įvesties faktorialą
- O(1) spausdinti kiekvienos įvesties faktorialą.
Atmintinės rūšys
Atminties įgyvendinimas priklauso nuo besikeičiančių parametrų, atsakingų už problemos sprendimą. Yra įvairių talpyklos matmenų, kurie naudojami atminties technikoje. Toliau pateikiami keli iš jų:
- 1D atmintinė: Rekursinė funkcija, turinti tik vieną argumentą, kurio reikšmė nebuvo pastovi po kiekvieno funkcijos iškvietimo.
- 2D atmintinė: Rekursinė funkcija, turinti tik du argumentus, kurių reikšmė nebuvo pastovi po kiekvieno funkcijos iškvietimo.
- 3D atmintinė : rekursinė funkcija, turinti tik tris argumentus, kurių reikšmės nebuvo pastovios po kiekvieno funkcijos iškvietimo.
Kaip memoization technika naudojama dinaminiame programavime?
Dinaminis programavimas padeda efektyviai išspręsti problemas, kurios turi persidengiančių poproblemų ir optimalių postruktūrų savybių. Dinaminio programavimo idėja yra suskaidyti problemą į smulkesnes problemas ir išsaugoti rezultatą naudoti ateityje, taip pašalinant poreikį pakartotinai skaičiuoti rezultatą.
Yra du dinaminio programavimo sprendimo būdai:
- Metodas iš viršaus į apačią: Šis požiūris atitinka atmintinė technika . Tai susideda iš rekursija ir talpykloje . Skaičiuojant rekursija reiškia pakartotinio funkcijų iškvietimo procesą, o talpykla reiškia tarpinių rezultatų saugojimo procesą.
- „Iš apačios į viršų“ metodas: Šis metodas naudoja lentelės sudarymas technika dinaminio programavimo sprendimui įgyvendinti. Jis sprendžia tas pačias problemas kaip ir anksčiau, bet be pasikartojimo. Taikant šį metodą, iteracija pakeičia rekursiją. Taigi nėra krūvos perpildymo klaidos ar rekursinių procedūrų papildomų išlaidų.
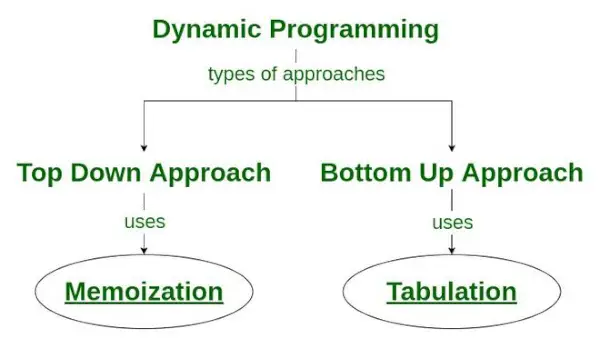
Kaip memoization technika naudojama dinaminiame programavime
Kuo Memoization skiriasi nuo lentelių sudarymo?

Lentelių sudarymas prieš atmintį
Daugiau informacijos rasite: Lentelių sudarymas prieš atmintį
Atmintinės kodavimo praktikos problemos
| Klausimas | Straipsnis | Praktika | Vaizdo įrašas |
|---|---|---|---|
| Suskaičiuokite būdus, kaip pasiekti n-tuosius laiptus | Žiūrėti | Išspręsti | Žiūrėti |
| Žodžių lūžio problema | DP-32 | Žiūrėti | Išspręsti | Žiūrėti |
| Fibonačio skaičių programa | Žiūrėti | Išspręsti | Žiūrėti |
| n-asis katalonų numeris | Žiūrėti | Išspręsti | Žiūrėti |
| Aukso kasyklos problema | Žiūrėti | Išspręsti | Žiūrėti |
| Pogrupio sumos problema | Žiūrėti | Išspręsti | Žiūrėti |
| Strypo pjovimas | Žiūrėti | Išspręsti | Žiūrėti |
| Minimalios kainos kelias | Žiūrėti | Išspręsti | Žiūrėti |
| Minimalus šuolių skaičius, kad pasiektumėte pabaigą | Žiūrėti | Išspręsti | Žiūrėti |
| Ilgiausia palindrominė eilutė | 1 rinkinys | Žiūrėti | Išspręsti | Žiūrėti |
| Ilgiausiai besikartojanti seka | Žiūrėti | Išspręsti | Žiūrėti |
| Suskaičiuokite būdus, kaip pasiekti n-tuosius laiptus, atlikdami 1, 2 arba 3 žingsnius | Žiūrėti | Išspręsti | Žiūrėti |
| Suskaičiuokite skirtingus būdus, kaip išreikšti N kaip 1, 3 ir 4 sumą | Žiūrėti | Išspręsti | Žiūrėti |
| Suskaičiuokite būdų, kaip įveikti atstumą, skaičių | Žiūrėti | Išspręsti | Žiūrėti |
| Masyvų, turinčių nuoseklų elementą su skirtingomis reikšmėmis, skaičius | Žiūrėti | Išspręsti | Žiūrėti |
| Didžiausios sumos gretimas pogrupis | Žiūrėti | Išspręsti | Žiūrėti |
| Mažiausios sumos gretimas pogrupis | Žiūrėti | Išspręsti | Žiūrėti |
| Unikalūs takai tinklelyje su kliūtimis | Žiūrėti | Išspręsti | Žiūrėti |
| Skirtingi būdai susumuoti n naudojant skaičius, didesnius arba lygius m | Žiūrėti | Išspręsti | Žiūrėti |
Dažniausiai užduodami klausimai (DUK) apie Memoization
1: Ar atmintis yra geriau nei DP?
Atmintinė yra metodas iš viršaus į apačią sprendžiant problemą naudojant dinaminį programavimą. Tai vadinama atmintine, nes mes sukursime atmintinę apie vertybes, grąžintas sprendžiant kiekvieną problemą.
2: ar atminties išsaugojimas yra tas pats, kas talpyklos kaupimas?
Iš tikrųjų atmintis yra specifinis talpyklos tipas. Terminas talpyklos kaupimas paprastai gali reikšti bet kokią saugojimo techniką (pvz., HTTP talpyklą), skirtą naudoti ateityje, tačiau atmintyje konkrečiau kalbama apie talpyklos funkciją, kuri grąžina vertę.
3: Kodėl atmintyje rašoma iš viršaus į apačią?
„Iš viršaus į apačią“ metodas suskaido didelę problemą į kelias dalis. jei poproblema jau išspręsta, naudokite atsakymą dar kartą. Kitu atveju išspręskite antrinę problemą ir išsaugokite rezultatą tam tikroje atmintyje.
4: Ar atmintyje naudojama rekursija?
Atmintyje sprendžiama problema iš viršaus į apačią. Jį sudaro rekursija ir talpyklos kaupimas. Skaičiuojant rekursija reiškia pakartotinio funkcijų iškvietimo procesą, o talpykla reiškia tarpinių rezultatų saugojimo procesą.
5: Ar turėčiau naudoti lentelę ar atmintinę?
Problemoms, kurias reikia išspręsti visoms antrinėms problemoms, lentelių sudarymas paprastai lenkia atmintį pastoviu koeficientu. Taip yra todėl, kad lentelėje nėra papildomos rekursijos, todėl sutrumpėja laikas, per kurį reikia išspręsti rekursijos iškvietimo krūvą iš dėklo atminties.
Kai reikia išspręsti subproblemą, kad būtų išspręsta pradinė problema, geriau įsiminti, nes poproblema sprendžiama atsainiai, t. y. atliekami tik reikalingi skaičiavimai.
6: Kur naudojama atmintis?
Atmintinė yra optimizavimo metodas, naudojamas paspartinti kompiuterių programas, talpinant brangių funkcijų iškvietimų rezultatus ir grąžinant juos, kai vėl susiduriama su ta pačia įvestimi.
7: Kodėl tai vadinama atmintimi?
Terminas „atmintis“ kilęs iš lotyniško žodžio „memorandum“ (atsiminti), kuris amerikiečių anglų kalboje paprastai sutrumpinamas į „memo“ ir reiškia funkcijos rezultatus paversti kažkuo, kurį reikia atsiminti.
8: Kaip atmintinė sumažina laiko sudėtingumą?
Vėl ir vėl tos pačios problemos sprendimas užtrunka ir padidina visos programos vykdymo laiką. Šią problemą galima išspręsti išlaikant tam tikrą talpyklą arba atmintį, kurioje išsaugosime jau apskaičiuotą problemos rezultatą tam tikram įėjimui. Taigi, jei nenorime perskaičiuoti tos pačios problemos, galime tiesiog panaudoti atmintyje saugomą rezultatą ir sumažinti laiko sudėtingumą.
9: Kuo skiriasi atmintinė ir talpyklos kaupimas?
Atmintinė iš tikrųjų yra specifinis talpyklos tipas, apimantis funkcijos grąžinimo vertės saugojimą talpykloje, pagrįstą įvestimi. Talpykla yra bendresnis terminas. Pavyzdžiui, HTTP talpyklos kaupimas talpykloje yra kaupimas talpykloje, bet ne atmintinė.
10: Kodėl lentelės sudarymas yra greitesnis nei įrašymas atmintyje?
Lentelių sudarymas paprastai yra greitesnis nei įrašymas į atmintį, nes jis kartojasi ir sprendžiant subproblemas nereikia papildomų rekursinių skambučių.
Atmintinė yra technika, naudojama kompiuterių moksle, siekiant pagreitinti rekursinių arba skaičiavimo požiūriu brangių funkcijų vykdymą, talpinant funkcijų iškvietimų rezultatus ir grąžinant talpykloje saugomus rezultatus, kai vėl atsiranda tie patys įėjimai.
Pagrindinė atmintinės idėja yra išsaugoti funkcijos išvestį tam tikram įėjimų rinkiniui ir grąžinti talpykloje esantį rezultatą, jei funkcija dar kartą iškviečiama naudojant tuos pačius įėjimus. Ši technika gali sutaupyti skaičiavimo laiko, ypač funkcijoms, kurios iškviečiamos dažnai arba kurių laikas yra labai sudėtingas.
Štai žingsnis po žingsnio vadovas, kaip įgyvendinti atmintinę:
Nustatykite funkciją, kurią norite optimizuoti naudodami atmintinę. Ši funkcija turi turėti pasikartojančius ir brangius tos pačios įvesties skaičiavimus.
Sukurkite žodyno objektą talpykloje saugomiems funkcijos rezultatams saugoti. Žodyno klavišai turėtų būti funkcijos įvesties parametrai, o reikšmės – apskaičiuoti rezultatai.
Funkcijos pradžioje patikrinkite, ar įvesties parametrai jau yra talpyklos žodyne. Jei taip, grąžinkite talpykloje išsaugotą rezultatą.
Jei įvesties parametrų nėra talpyklos žodyne, apskaičiuokite rezultatą ir išsaugokite jį talpyklos žodyne naudodami įvesties parametrus kaip raktą.
Grąžinkite apskaičiuotą rezultatą.
Štai Python kodo pavyzdys, kaip įdiegti atmintinę naudojant žodyną:
Python3
rūšiuoti krūvą
def> fibonacci(n, cache>=>{}):> >if> n>in> cache:> >return> cache[n]> >if> n>=>=> 0>:> >result>=> 0> >elif> n>=>=> 1>:> >result>=> 1> >else>:> >result>=> fibonacci(n>->1>)>+> fibonacci(n>->2>)> >cache[n]>=> result> >return> result> |
>
>Išvestis
>
Aukščiau pateiktame kode apibrėžiame funkciją, vadinamą fibonačio, kuri apskaičiuoja n-ąjį skaičių Fibonačio sekoje. Funkcijų iškvietimų rezultatams saugoti naudojame žodyno objektą, vadinamą cache. Jei įvesties parametras n jau yra talpyklos žodyne, mes grąžiname talpykloje išsaugotą rezultatą. Kitu atveju rezultatą apskaičiuojame naudodami rekursinius fibonačio funkcijos iškvietimus ir išsaugome jį talpyklos žodyne prieš grąžindami.
Atmintinė gali būti naudojama norint optimizuoti daugelio funkcijų, kurios turi pasikartojančius ir brangius skaičiavimus, veikimą. Talpindami funkcijų iškvietimų rezultatus, galime išvengti nereikalingų skaičiavimų ir pagreitinti funkcijos vykdymą.
Išvada
Memoization yra programavimo koncepcija ir gali būti taikoma bet kuriai programavimo kalbai. Jo absoliutus tikslas yra optimizuoti programą. Paprastai ši problema pastebima, kai programos atlieka sunkius skaičiavimus. Ši technika talpina visus ankstesnius apskaičiuotus rezultatus, kad nereikėtų perskaičiuoti tos pačios problemos.
Susiję straipsniai:
- Atmintis naudojant dekoratorius Python
- „JavaScript“ atmintinė
