Dvejetainis paieškos medis yra duomenų struktūra, naudojama kompiuterių moksle duomenims rūšiuoti ir saugoti. Dvejetainis paieškos medis seka visas dvejetainio medžio ir jo savybes paliko vaikas turi mažesnes reikšmes nei pirminis mazgas ir teisingai vaikas turi didesnes reikšmes nei pirminis mazgas. Ši hierarchinė struktūra leidžia efektyviai Ieškoma , Įdėjimas , ir Ištrynimas operacijos su medyje saugomais duomenimis.

Dvejetainis paieškos medis

Turinys

• Kas yra dvejetainis paieškos medis?
• Dvejetainės paieškos medžio savybės
• Pasikartojančių reikšmių tvarkymas dvejetainėje paieškos medyje
• BST atliekamos operacijos
• 1. Mazgo paieška BST
• 2. Įdėkite mazgą į BST
• 3. Ištrinkite BST mazgą
• 4. Traversal (BST perėjimas į eilę)
• BST programos
• Privalumai
• Trūkumai
• DUK (dažniausiai užduodami klausimai) dvejetainėje paieškos medyje:

Kas yra dvejetainis paieškos medis?

Dvejetainis paieškos medis (BST) yra ypatingas tipas dvejetainis medis kai kairiojo mazgo antrinio elemento reikšmė yra mažesnė už mazgo vertę, o dešiniojo antrininko reikšmę yra didesnė už mazgo vertę. Ši savybė vadinama BST nuosavybe ir leidžia efektyviai ieškoti, įterpti ir ištrinti elementus medyje.

Dvejetainės paieškos medžio savybės:

• Kairiajame mazgo pomedyje yra tik mazgai, kurių raktai yra mažesni už mazgo raktą.
• Dešiniajame mazgo pomedyje yra tik mazgai, kurių raktai yra didesni už mazgo raktą.
• Tai reiškia, kad viskas, kas yra kairėje nuo šaknies, yra mažesnė už šaknies vertę, o viskas, kas yra šaknies dešinėje, yra didesnė už šaknies vertę. Dėl šio atlikimo dvejetainė paieška yra labai paprasta.
• Kairysis ir dešinysis pomedžiai taip pat turi būti dvejetainis paieškos medis.
• Neturi būti pasikartojančių mazgų (BST gali turėti pasikartojančias vertes su skirtingais tvarkymo būdais)

Pasikartojančių verčių tvarkymas dvejetainėje paieškos medyje:

• Turime laikytis nuoseklaus proceso, t. y. arba saugoti pasikartojančią vertę kairėje, arba pasikartojančią vertę šaknies dešinėje, tačiau laikytis savo požiūrio.

Pagrindinės dvejetainės paieškos medžio operacijos:

1. Mazgo paieška BST:

Ieškoti BST reiškia konkretaus mazgo vietą duomenų struktūroje. Dvejetainėje paieškos medyje mazgo paieška yra paprasta dėl konkrečios tvarkos. Mazgo paieškos dvejetainės paieškos medyje žingsniai išvardyti taip –

1. Pirmiausia palyginkite ieškomą elementą su medžio šaknies elementu.
   • Jei šaknis atitinka tikslinį elementą, grąžinkite mazgo vietą.
   • Jei jis nesutampa, patikrinkite, ar elementas yra mažesnis už šakninį elementą, jei jis mažesnis už šakninį elementą, tada pereikite į kairįjį pomedį.
   • Jei jis didesnis nei šakninis elementas, pereikite prie dešiniojo pomedžio.
2. Kartokite aukščiau aprašytą procedūrą rekursyviai, kol bus rastas atitikmuo.
3. Jei elementas nerastas arba jo nėra medyje, grąžinkite NULL.

Dabar supraskime paiešką dvejetainiame medyje naudodami pavyzdį:

Žemiau pateikiamas BST ir turime ieškoti 6 elemento.

Kodas:

Žemiau pateikiamas paieškos BST įgyvendinimas:

// C++ function to search a given key in a given BST #include  using namespace std; struct node {  int key;  struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) {  struct node* temp  = new struct node;  temp->raktas = prekė;  temp->left = temp->right = NULL;  grąžinimo temperatūra; } // Naudingumo funkcija įterpti // naują mazgą su duotu raktu į BST struct node* insert(struct node* node, int key) { // Jei medis tuščias, grąžinkite naują mazgą if (mazgas == NULL ) return newNode(raktas);  // Priešingu atveju pakartokite medį, jei (key< node->raktas) mazgas->kairė = įterpti(mazgas->kairysis, raktas);  else if (raktas> mazgas->raktas) mazgas->dešinė = insert(mazgas->dešinė, raktas);  // Grąžinti (nepakeistą) mazgo rodyklę return node; } // Naudingumo funkcija ieškoti rakto BST struct node* search(struct node* root, int key) root->key == key) return root;  // Raktas yra didesnis nei šakninis raktas if (root->key< key)  return search(root->dešinėje, raktas);  // Raktas yra mažesnis nei root's key return search(root->left, key);>>C 
// Java program to search a given key in a given BST class Node {  int key;  Node left, right;  public Node(int item) {  key = item;  left = right = null;  } } class BinarySearchTree {  Node root;  // Constructor  BinarySearchTree() {  root = null;  }  // A utility function to insert  // a new node with given key in BST  Node insert(Node node, int key) {  // If the tree is empty, return a new node  if (node == null) {  node = new Node(key);  return node;  }  // Otherwise, recur down the tree  if (key < node.key)  node.left = insert(node.left, key);  else if (key>mazgas.raktas) mazgas.dešinė = įterpti(mazgas.dešinė, raktas);  // Grąžinti (nepakeistą) mazgo rodyklę return node;  } // Naudingumo funkcija ieškoti rakto BST mazgo paieškoje (mazgo šaknis, int raktas) // Pagrindiniai atvejai: šaknis yra nulis arba raktas yra šaknyje if (root == null>
 Python 
# Python3 function to search a given key in a given BST class Node: # Constructor to create a new node def __init__(self, key): self.key = key self.left = None self.right = None # A utility function to insert # a new node with the given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(mazgas.dešinė, raktas) # Grąžinti (nepakeistą) mazgo rodyklės grąžinimo mazgą # Naudingumo funkcija, skirta ieškoti rakto BST def paieškoje (šaknis, raktas): # Pagrindiniai atvejai: šaknis yra Nulis arba raktas yra šaknyje, jei root yra None arba root.key == raktas: return root # Key yra didesnis nei root's key, jei root.key< key: return search(root.right, key) # Key is smaller than root's key return search(root.left, key)>
 JavaScript 
// Javascript function to search a given key in a given BST class Node { constructor(key) {  this.key = key;  this.left = null;  this.right = null; } } // A utility function to insert // a new node with given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node === null) {  return new Node(key); } // Otherwise, recur down the tree if (key < node.key) {  node.left = insert(node.left, key); } else if (key>mazgas.raktas) { mazgas.dešinė = įterpti(mazgas.dešinė, raktas); } // Grąžina (nepakeistą) mazgo rodyklės grąžinimo mazgą; } // Naudingumo funkcija, skirta ieškoti rakto BST funkcijos paieškoje (šaknis, raktas) { // Pagrindiniai atvejai: šaknis yra nulis arba raktas yra šaknyje if (root === null || root.key === raktas ) { grąžinti šaknį; } // Raktas yra didesnis nei šakninis raktas if (root.key< key) {  return search(root.right, key); } // Key is smaller than root's key return search(root.left, key); }>
  
  
 
    2.         Įdėkite mazgą į BST         :     
Prie lapo visada įkišamas naujas raktas. Pradėkite ieškoti rakto nuo šaknies iki lapo mazgo. Kai randamas lapo mazgas, naujas mazgas pridedamas kaip lapo mazgo antrinis.
 
  
 
    Kodas:    
Java pavadinimų sutartys
 
Žemiau pateikiamas vieno mazgo įterpimo į dvejetainį paieškos medį įgyvendinimas:
C++ 
// Given Node Structure struct node {  int key;  struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) {  struct node* temp = (struct node*)malloc(  sizeof(struct node));  temp->raktas = prekė;  temp->left = temp->right = NULL;  grąžinimo temperatūra; } // Funkcija įterpti naują mazgą su // duotu raktu BST struct node* insert(struct node* node, int key) { // Jei medis tuščias, grąžinkite naują mazgą if (node ​​== NULL) return newMazgas(raktas);  // Priešingu atveju pakartokite medį, jei (key< node->raktas) { mazgas->kairė = įterpti(mazgas->kairysis, raktas);  } else if (raktas> mazgas->raktas) { mazgas->dešinė = įterpti(mazgas->dešinė, raktas);  } // Return the node pointer return node; }>
 C 
// Given Node Structure struct node {  int key;  struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) {  struct node* temp  = (struct node*)malloc(  sizeof(struct node));  temp->raktas = prekė;  temp->left = temp->right = NULL;  grąžinimo temperatūra; } // Funkcija įterpti naują mazgą su // duotu raktu BST struct node* insert(struct node* node, int key) { // Jei medis tuščias, grąžinkite naują mazgą if (node ​​== NULL) return newMazgas(raktas);  // Priešingu atveju pakartokite medį, jei (key< node->raktas) { mazgas->kairė = įterpti(mazgas->kairysis, raktas);  } else if (raktas> mazgas->raktas) { mazgas->dešinė = įterpti(mazgas->dešinė, raktas);  } // Return the node pointer return node; }>
 Java 
class GFG {  // Given Node Structure  static class node {  int key;  node left, right;  };  // Function to create a new BST node  static node newNode(int item)  {  node temp = new node();  temp.key = item;  temp.left = temp.right = null;  return temp;  }  // Function to insert a new node with  // given key in BST  static node insert(node node, int key)  {  // If the tree is empty, return a new node  if (node == null)  return newNode(key);  // Otherwise, recur down the tree  if (key < node.key) {  node.left = insert(node.left, key);  }  else if (key>mazgas.raktas) { mazgas.dešinė = įterpti(mazgas.dešinė, raktas);  } // Return the node return node;  } }>>Python3 
// Given Node Structure class Node {  constructor(key){  this.key = key;  this.left = null;  this.right = null;  } } // Function to insert a new node with // given key in BST function insert(node, key) {    // If the tree is empty, return a new node  if (node == null)  return new Node(key);  // Otherwise, recur down the tree  if (key < node.key)  {  node.left = insert(node.left, key);  }  else if (key>mazgas.raktas) { mazgas.dešinė = įterpti(mazgas.dešinė, raktas);  } // Return the node pointer return node; }>
  
    Laiko sudėtingumas:    O(N), kur N yra BST mazgų skaičius  
    Pagalbinė erdvė:    O(1)
 
    3.          Ištrinkite BST mazgą     :
Jis naudojamas norint ištrinti mazgą su konkrečiu raktu iš BST ir grąžinti naują BST.
 
Įvairūs mazgo ištrynimo scenarijai:
 
    Mazgas, kurį reikia ištrinti, yra lapo mazgas       :    
Tai paprasta, jūs galite tiesiog jį panaikinti.
  
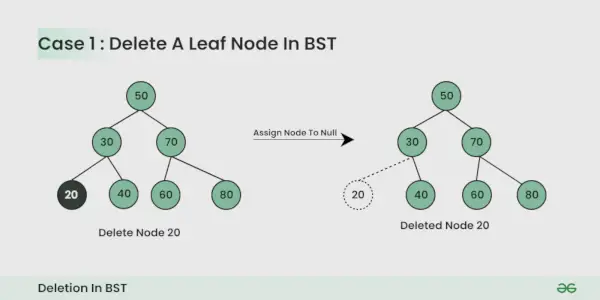
    Ištrintiname mazge yra vienas vaikas       :     
Galite tiesiog pakeisti mazgą antriniu mazgu.
  
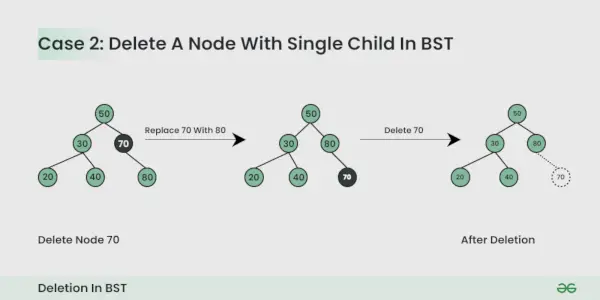
    Ištrintiname mazge yra du vaikai       :     
Čia mes turime    Ištrinkite mazgą tokiu būdu, kad gautas medis atitiktų BST savybes.    Triukas yra rasti netvarkingą mazgo įpėdinį. Nukopijuokite eilės įpėdinio turinį į mazgą ir ištrinkite eilės įpėdinį.
  
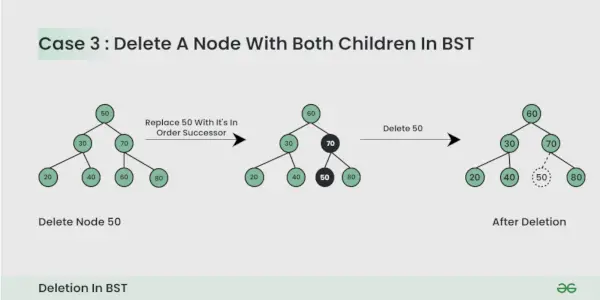
Ištrindami BST mazgą, atkreipkite dėmesį į šiuos dalykus:
 
Reikia išsiaiškinti, koks bus ištrinamo mazgo pakeitimas.
Norite kuo mažiau trikdyti esamą medžio struktūrą
Gali paimti pakaitinį mazgą iš ištrintų mazgų kairiajame arba dešiniajame pomedžio.
Jei imame iš kairiojo pomedžio, didžiausią reikšmę turime paimti kairiajame pomedžiu.
Jei imame iš dešiniojo pomedžio, turime paimti mažiausią dešiniojo pomedžio reikšmę.
    Kodas:    
 
Toliau pateikiamas BST ištrynimo įgyvendinimas:
C++ 
// C++ program to delete // a node of BST // Given Node node struct node {  int key;  struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) {  struct node* temp  = (struct node*)malloc(  sizeof(struct node));  temp->raktas = prekė;  temp->left = temp->right = NULL;  grąžinimo temperatūra; } // Funkcija įterpti naują mazgą su // duotu raktu BST struct node* insert(struct node* node, int key) { // Jei medis tuščias, grąžinkite naują mazgą if (node ​​== NULL) return newMazgas(raktas);  // Priešingu atveju pakartokite medį, jei (key< node->raktas) { mazgas->kairė = įterpti(mazgas->kairysis, raktas);  } else if (raktas> mazgas->raktas) { mazgas->dešinė = įterpti(mazgas->dešinė, raktas);  } // Return the node pointer return node; } // Funkcija, kuri grąžina mazgą su mažiausia // rakto reikšme, rasta tame medyje struct node* minValueNode(struct node* node) { struct node* current = node;  // Sukite žemyn, kad rastumėte kairįjį lapą, o (dabartinis && srovė->kairysis != NULL) current = current->left;  grąžinimo srovė; } // Funkcija, kuri ištrina raktą ir // grąžina naują šakninį struct node* deleteNode(struct node* root, int key) { // Base Case if (root == NULL) return root;  // Jei norimas ištrinti raktas yra // mažesnis už šakninį raktą, // tada jis yra kairiajame pomedyje if (key< root->raktas) { root->left = deleteNode(root->left, key);  } // Jei norimas ištrinti raktas yra // didesnis nei šakninis raktas, // tada jis yra dešiniajame pomedyje else if (raktas> šaknis->raktas) { root->right = deleteNode(root-> dešinėje, raktas);  } // Jei raktas yra toks pat kaip root's raktas, // tada tai mazgas //, kurį reikia ištrinti. Kitaip { // Mazgas su tik vienu antruoju // arba be vaiko, jei (root->left == NULL) { struct mazgas* temp = root->right;  laisvas(šaknis);  grąžinimo temperatūra;  } else if (root->right == NULL) { struct mazgas* temp = root->left;  laisvas(šaknis);  grąžinimo temperatūra;  } // Mazgas su dviem vaikais: // Gauti eilės įpėdinį (mažiausias // dešiniajame pomedyje) struct node* temp = minValueNode(root->right);  // Nukopijuokite eilės įpėdinio // turinį į šį mazgą root->key = temp->key;  // Ištrinti eilės įpėdinį root->right = deleteNode(root->right, temp->key);  } return root; }>
 C 
// C program to delete // a node of BST // Given Node node struct node {  int key;  struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) {  struct node* temp  = (struct node*)malloc(  sizeof(struct node));  temp->raktas = prekė;  temp->left = temp->right = NULL;  grąžinimo temperatūra; } // Funkcija įterpti naują mazgą su // duotu raktu BST struct node* insert(struct node* node, int key) { // Jei medis tuščias, grąžinkite naują mazgą if (node ​​== NULL) return newMazgas(raktas);  // Priešingu atveju pakartokite medį, jei (key< node->raktas) { mazgas->kairė = įterpti(mazgas->kairysis, raktas);  } else if (raktas> mazgas->raktas) { mazgas->dešinė = įterpti(mazgas->dešinė, raktas);  } // Return the node pointer return node; } // Funkcija, kuri grąžina mazgą su mažiausia // rakto reikšme, rasta tame medyje struct node* minValueNode(struct node* node) { struct node* current = node;  // Sukite žemyn, kad rastumėte kairįjį lapą, o (dabartinis && srovė->kairysis != NULL) current = current->left;  grąžinimo srovė; } // Funkcija, kuri ištrina raktą ir // grąžina naują šakninį struct node* deleteNode(struct node* root, int key) { // Base Case if (root == NULL) return root;  // Jei norimas ištrinti raktas yra // mažesnis nei šakninis raktas, // tada jis yra kairiajame pomedyje if (klavišas< root->raktas) { root->left = deleteNode(root->left, key);  } // Jei norimas ištrinti raktas yra // didesnis nei šakninis raktas, // tada jis yra dešiniajame pomedyje else if (raktas> šaknis->raktas) { root->right = deleteNode(root-> dešinėje, raktas);  } // Jei raktas yra toks pat kaip root's raktas, // tada tai mazgas //, kurį reikia ištrinti. Kitaip { // Mazgas su tik vienu antruoju // arba be vaiko, jei (root->left == NULL) { struct mazgas* temp = root->right;  laisvas(šaknis);  grąžinimo temperatūra;  } else if (root->right == NULL) { struct mazgas* temp = root->left;  laisvas(šaknis);  grąžinimo temperatūra;  } // Mazgas su dviem vaikais: // Gauti eilės įpėdinį (mažiausias // dešiniajame pomedyje) struct node* temp = minValueNode(root->right);  // Nukopijuokite eilės įpėdinio // turinį į šį mazgą root->key = temp->key;  // Ištrinti eilės įpėdinį root->right = deleteNode(root->right, temp->key);  } return root; }>
 Java 
// Java program for Delete a Node of BST class GFG {  // Given Node node  static class node {  int key;  node left, right;  };  // Function to create a new BST node  static node newNode(int item)  {  node temp = new node();  temp.key = item;  temp.left = temp.right = null;  return temp;  }  // Function to insert a new node with  // given key in BST  static node insert(node node, int key)  {  // If the tree is empty, return a new node  if (node == null)  return newNode(key);  // Otherwise, recur down the tree  if (key < node.key) {  node.left = insert(node.left, key);  }  else if (key>mazgas.raktas) { mazgas.dešinė = įterpti(mazgas.dešinė, raktas);  } // Return the node return node;  } // Funkcija, kuri grąžina mazgą su mažiausia // rakto reikšme, rasta tame medyje statiniame mazge minValueNode(mazgo mazgas) { mazgo srovė = mazgas;  // Sukite žemyn, kad rastumėte kairįjį lapą, o (current != null && current.left != null) current = current.left;  grąžinimo srovė;  } // Funkcija, kuri ištrina raktą ir // grąžina naują šakninį statinį mazgą deleteNode(mazgo šaknis, int raktas) { // Base Case if (root == null) return root;  // Jei norimas ištrinti raktas yra // mažesnis už šakninį raktą, // tada jis yra kairiajame pomedyje if (key< root.key) {  root.left = deleteNode(root.left, key);  }  // If the key to be deleted is  // greater than the root's key,  // then it lies in right subtree  else if (key>root.key) { root.right = deleteNode(root.right, key);  } // Jei raktas yra toks pat kaip root's raktas, // tada tai mazgas //, kuris turi būti ištrintas else { // Mazgas su tik vienu antruoju // arba be vaiko if (root.left == null) { mazgo temp = root.right;  grąžinimo temperatūra;  } else if (root.right == null) { mazgo temp = root.left;  grąžinimo temperatūra;  } // Mazgas su dviem vaikais: // Gauti eilės įpėdinį (mažiausias // dešiniajame pomedyje) mazgas temp = minValueNode(root.right);  // Nukopijuokite eilės įpėdinio // turinį į šį mazgą root.key = temp.key;  // Ištrinti eilės įpėdinį root.right = deleteNode(root.right, temp.key);  } return root;  }>
 Python 
# Python program to delete a node of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(root, key): # If the tree is empty, return a new node if root is None: return Node(key) # Otherwise, recur down the tree if key < root.key: root.left = insert(root.left, key) elif key>root.key: root.right = insert(root.right, key) # Grąžina mazgo rodyklę return root # Funkcija, skirta atlikti inorder perėjimą BST def inorder(root): if root: inorder(root.left) print(root. key, end=' ') inorder(root.right) # Funkcija, kuri grąžina mazgą su mažiausia # rakto reikšme, esančia tame medyje def minValueNode(mazgas): current = node # Kilo žemyn, kad surastumėte kairiausią lapą, kol esama ir current.left nėra None: current = current.left return current # Funkcija, kuri ištrina raktą ir # grąžina naują root def deleteNode(root, key): # bazinis atvejis, jei šaknis yra Nėra: return root # Jei raktas turi būti ištrintas yra # mažesnis už šakninį raktą, # tada jis yra kairiajame pomedyje, jei raktas< root.key: root.left = deleteNode(root.left, key) # If the key to be deleted is # greater than the root's key, # then it lies in right subtree elif key>root.key: root.right = deleteNode(root.right, key) # Jei raktas yra toks pat kaip root raktas, # tada tai mazgas #, kuris turi būti ištrintas kitu atveju: # Mazgas tik su vienu vaiku # arba be vaiko jei root.left yra Nėra: temp = root.right root = Nėra grąžinimo temp elif root.right yra Nėra: temp = root.left root = Nėra grąžinimo temp # Mazgas su dviem vaikais: # Gaukite eilės įpėdinį (mažiausią # dešinysis pomedis) temp = minValueNode(root.right) # Nukopijuokite eilės įpėdinio # turinį į šį mazgą root.key = temp.key # Ištrinkite eilės įpėdinį root.right = deleteNode(root.right, temp.key) grąžinti šaknį>>> 
    4.         „Traversal“ (BST įsakymas)         :    
Dvejetainių paieškos medžių (BST) atveju Inorder traversal pateikia mazgus nemažėjančia tvarka. Pirmiausia aplankome kairįjį vaiką, tada šaknį, o tada dešinį vaiką.
turbo c++ parsisiųsti
 
Žemiau pateikiama, kaip atlikti dvejetainio paieškos medžio perėjimą:
C++Raktas;  inorder(root->right);  } } // Tvarkyklės kodas int main() { /* Sukurkime šiuos BST 50 /  30 70 /  /  20 40 60 80 */ struct node* root = NULL;  // BST šaknies kūrimas = insert(root, 50);  įterpti(šaknis, 30);  įterpti(šaknis, 20);  įterpti(šaknis, 40);  įterpti(šaknis, 70);  įterpti(šaknis, 60);  įterpti(šaknis, 80);  // Funkcija Call inorder(root);  grąžinti 0; } // Šį kodą sukūrė shivanisinghss2110>
 C 
// C program to implement // inorder traversal of BST #include  #include  // Given Node node struct node {  int key;  struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) {  struct node* temp  = (struct node*)malloc(  sizeof(struct node));  temp->raktas = prekė;  temp->left = temp->right = NULL;  grąžinimo temperatūra; } // Funkcija įterpti naują mazgą su // duotu raktu BST struct node* insert(struct node* node, int key) { // Jei medis tuščias, grąžinkite naują mazgą if (node ​​== NULL) return newMazgas(raktas);  // Priešingu atveju pakartokite medį, jei (key< node->raktas) { mazgas->kairė = įterpti(mazgas->kairysis, raktas);  } else if (raktas> mazgas->raktas) { mazgas->dešinė = įterpti(mazgas->dešinė, raktas);  } // Return the node pointer return node; } // Funkcija atlikti inorder perėjimą BST void inorder(struct node* root) { if (root != NULL) { inorder(root->left);  printf('%d ', root->key);  inorder(root->right);  } } // Tvarkyklės kodas int main() { /* Sukurkime šiuos BST 50 /  30 70 /  /  20 40 60 80 */ struct node* root = NULL;  // BST šaknies kūrimas = insert(root, 50);  įterpti(šaknis, 30);  įterpti(šaknis, 20);  įterpti(šaknis, 40);  įterpti(šaknis, 70);  įterpti(šaknis, 60);  įterpti(šaknis, 80);  // Funkcija Call inorder(root);  grąžinti 0; }>
 Java 
import java.io.*; // Java program for Inorder Traversal class GFG {  // Given Node node  static class node {  int key;  node left, right;  };  // Function to create a new BST node  static node newNode(int item)  {  node temp = new node();  temp.key = item;  temp.left = temp.right = null;  return temp;  }  // Function to insert a new node with  // given key in BST  static node insert(node node, int key)  {  // If the tree is empty, return a new node  if (node == null)  return newNode(key);  // Otherwise, recur down the tree  if (key < node.key) {  node.left = insert(node.left, key);  }  else if (key>mazgas.raktas) { mazgas.dešinė = įterpti(mazgas.dešinė, raktas);  } // Return the node return node;  } // Funkcija atlikti BST inorder perėjimą static void inorder(mazgo šaknis) { if (root != null) { inorder(root.left);  System.out.print(' ' + root.key);  inorder(root.right);  } } // Tvarkyklės kodas public static void main(String[] args) { /* Sukurkime šiuos BST 50 /  30 70 /  /  20 40 60 80 */ mazgas root = null;  // įterpiant reikšmę 50 root = insert(root, 50);  // įterpiant reikšmę 30 insert(root, 30);  // įterpiant reikšmę 20 insert(root, 20);  // įterpiant reikšmę 40 insert(root, 40);  // įterpiant reikšmę 70 insert(root, 70);  // įterpiant reikšmę 60 insert(root, 60);  // įterpiant reikšmę 80 insert(root, 80);  // atspausdinti BST inorder(root);  } } // Šį kodą sukūrė abhijitjadhav1998>
 Python3 
# Python program to implement # inorder traversal of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to create a new BST node def newNode(item): temp = Node(item) temp.key = item temp.left = temp.right = None return temp # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return newNode(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(mazgas.dešinė, raktas) # Grąžinti mazgo rodyklę return mazgas # Funkcija, skirta atlikti inorder perėjimą BST def inorder(root): if root: inorder(root.left) print(root. raktas, end=' ') inorder(root.right) # Tvarkyklės kodas if __name__ == '__main__': # Sukurkime šį BST # 50 # /  # 30 70 # /  /  # 20 40 60 80 root = Nėra # BST šaknies kūrimas = insert(root, 50) insert(root, 30) insert(root, 20) insert(root, 40) insert(root, 70) insert(root, 60) insert(root, 60) , 80) # Funkcija Call inorder(root) #Šį kodą įdėjo japmeet01>>  
  Išvestis      Laiko sudėtingumas:    O(N), kur N yra BST mazgų skaičius  
    Pagalbinė erdvė:    O(1)
 
    BST taikymas:    
    Grafiniai algoritmai:    BST gali būti naudojami grafikų algoritmams įgyvendinti, pvz., minimalaus apimančio medžio algoritmuose.
    Prioritetinės eilės:    BST gali būti naudojamas diegiant prioritetines eiles, kai didžiausią prioritetą turintis elementas yra medžio šaknyje, o žemesnio prioriteto elementai saugomi pomedžiuose.
    Savaime balansuojantis dvejetainis paieškos medis:    BST gali būti naudojamos kaip savaime balansuojančios duomenų struktūros, tokios kaip AVL medis ir raudonai juodas medis.
    Duomenų saugojimas ir gavimas:    BST galima naudoti norint greitai saugoti ir gauti duomenis, pavyzdžiui, duomenų bazėse, kur konkretaus įrašo paieška gali būti atliekama logaritminiu laiku.
    Privalumai:    
    Greita paieška:    Ieškant konkrečios reikšmės BST, vidutinis laiko sudėtingumas yra O(log n), kur n yra medžio mazgų skaičius. Tai daug greičiau nei ieškoti elemento masyve arba susietame sąraše, kurio laiko sudėtingumas blogiausiu atveju yra O(n).
    Perėjimas pagal užsakymą:    BST galima pereiti tokia tvarka, kuri aplanko kairįjį pomedį, šaknį ir dešinįjį pomedį. Tai gali būti naudojama duomenų rinkiniui rūšiuoti.
    Erdvės taupymas:    BST taupo erdvę, nes nesaugo jokios perteklinės informacijos, kitaip nei masyvuose ir susietuose sąrašuose.
    Trūkumai:    
    Iškreipti medžiai:    Jei medis bus iškreiptas, paieškos, įterpimo ir ištrynimo operacijų laiko sudėtingumas bus O(n), o ne O(log n), todėl medis gali būti neefektyvus.
    Reikalingas papildomas laikas:    Savaime išsibalansuojantiems medžiams reikia papildomo laiko, kad išlaikytų pusiausvyrą atliekant įterpimo ir ištrynimo operacijas.
    Efektyvumas:    BST nėra veiksmingi duomenų rinkiniams su daugybe dublikatų, nes jie eikvoja vietą.
DUK(Dažnai užduodami klausimai)dvejetainėje paieškos medyje:
    1. Kas yra dvejetainis paieškos medis?    
 
Dvejetainis paieškos medis (BST) yra    dvejetainis medis, kuriame kiekvienas kairiojo pomedžio mazgas yra mažesnis už šaknį, o kiekvieno dešiniojo pomedžio mazgo vertė yra didesnė už šaknį    . Dvejetainio paieškos medžio savybės yra rekursinės: jei bet kurį mazgą laikysime šaknimis, šios savybės išliks teisingos.
 
2. Kas yra dvejetainės paieškos medžio operacija?
 
Dvejetainėje paieškos medyje yra trys pagrindinės operacijos:    1. Įterpimas, 2. Ištrynimas, 3. Paieška.    Dėl savo savybių efektyviai galima ieškoti bet kurio elemento dvejetainiame paieškos medyje.
 
3. Kas yra dvejetainis paieškos medis ir AVL medis?
 
    Dvejetainis paieškos medis       :    Dvejetainis paieškos medis (BST) yra dvejetainis medis, kuriame kiekvienas kairiojo pomedžio mazgas yra mažesnis už šaknį, o kiekvieno dešiniojo pomedžio mazgo vertė yra didesnė už šaknį.
 
    AVL medis       :    Dvejetainiai paieškos medžiai (BST), kurie savaime susibalansuoja ir sukasi automatiškai, yra žinomi kaip AVL medžiai.
 
4. Kam naudojamas dvejetainis paieškos medis?
 
Dvejetainiai paieškos medžiai gali būti naudojami abstrakčių duomenų tipams įgyvendinti, pvz    dinaminiai rinkiniai, paieškos lentelės ir prioritetinės eilės,    ir naudojamas    rūšiavimo algoritmai    pavyzdžiui, medžių rūšiavimas.
 
5. Kuo skiriasi dvejetainis paieškos medis nuo dvejetainio medžio?
 
Dvejetainis paieškos medis yra medis, kuris pagal tam tikrą elementų išdėstymo tvarką, o dvejetainis medis nesilaiko jokios tvarkos.
 
    Susiję straipsniai:    
 
     BST taikymas     
     Dvejetainės paieškos medžio programos, privalumai ir trūkumai     
     Įterpimas į dvejetainį paieškos medį (BST)     
     Paieška dvejetainiame paieškos medyje (BST)     
     Ištrynimas dvejetainiame paieškos medyje (BST)