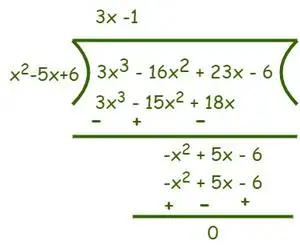Kubinė lygtis yra matematinė lygtis, kurioje 3 laipsnio polinomas prilyginamas konstantai arba kitam didžiausio 2 laipsnio daugianariui. Standartinis kubinės lygties vaizdas yra kirvis ³ +bx ² +cx+d = 0 kur a, b, c ir d yra realieji skaičiai. Kai kurie kubinių lygčių pavyzdžiai yra x ³ – 4x ² + 15x – 9 = 0, 2x ³ – 4x ² = 0 ir tt

Turinys

• Polinomo apibrėžimas
• Lygties laipsnis
• Kubinės lygties apibrėžimas
• Kaip išspręsti kubines lygtis?
• Kubinių lygčių sprendimas
• Kubinių lygčių sprendimas naudojant veiksnius
• Kubinių lygčių sprendimas grafiniu metodu
• Kubinių lygčių sprendimo uždaviniai
• Praktikos uždaviniai sprendžiant kubines lygtis

Norėdami išmokti išspręsti kubines lygtis, pirmiausia turime sužinoti apie daugianario laipsnį, daugianario laipsnį ir kt. Šiame straipsnyje mes išsamiai sužinosime apie polinomus, polinomines lygtis, kubinių lygčių sprendimą arba kaip išspręsti kubines lygtis ir kitus dalykus.

Polinomo apibrėžimas

Polinomas apibrėžiamas taip,

A daugianario yra algebrinė išraiška, kurioje kintamojo galia yra neneigiamas sveikasis skaičius. Bendroji daugianario forma yra a₀xⁿ+ a₁x^n-1+ a₂x^n-2+… + a_n. Priklausomai nuo didžiausios kintamojo galios, daugianarį galima suskirstyti į vienanarį, dvinarį, trinarį ir pan.

Kas yra lygtis?

Lygtis apibrėžiama taip,

Lygtis yra daugianomas, kuris prilyginamas skaitinei reikšmei arba bet kuriam kitam daugianariui. Pavyzdžiui, x + 2 yra daugianomas, o x + 2 = 5 yra lygtis. Panašiai 2x + 3 = x + 1 taip pat yra lygtis, o 2x + 3 ir x + 1 yra daugianariai atskirai.

Lygties laipsnis

Lygties laipsnio apibrėžimas pateiktas žemiau:

Lygties laipsnis apibrėžiamas kaip maksimali galia, kurią turi lygties kintamasis.

Remiantis lygties laipsniu, lygtis gali būti klasifikuojama taip:

• Tiesinė lygtis
• Kvadratinė lygtis
• Kubinė lygtis
• Bikvadratinė lygtis

Tiesinė lygtis

Lygtis, kurioje didžiausia kintamojo galia yra 1, vadinama tiesine lygtimi.

• Pavyzdžiui, 3x +1 = 0

Kvadratinis polinomas

Lygtis, kurioje didžiausia kintamojo galia yra 2, yra kvadratinė lygtis.

• Pavyzdžiui 3x²+x+1 = 0

Kubinė lygtis

Lygtis, kurioje didžiausia kintamojo galia yra 3, vadinama kubine lygtimi.

• Pavyzdžiui 5x³+3x²+x+1 = 0

Bikvadratinis polinomas

Lygtis, kurioje didžiausia kintamojo galia yra 4, vadinama bikvadratiniu polinomu arba kvartiniu polinomu.

• Pavyzdžiui 5x⁴+4x³+3x²+2x+1 = 0

Kubinės lygties apibrėžimas

Kubinė lygtis yra algebrinė lygtis, kurioje didžiausias daugianario laipsnis yra 3. Kai kurie kubinių lygčių pavyzdžiai yra 5x³+3x²+x+1 = 0, 2x³+8 = x ⇒ 2x³-x+8 = 0 ir kt.

Bendroji kubinės lygties forma yra

kirvis ³ + bx ² + cx + d = 0, a ≠ 0

kur,

• a, b, ir c yra kintamojo koeficientai ir jų eksponentai ir d yra konstanta ir
• a, b, c ir d yra realūs skaičiai.

Kaip išspręsti kubines lygtis?

Kubinė lygtis yra lygtis su trečiuoju laipsniu. Jame yra trys sprendimai ir jį galima lengvai išspręsti atlikus toliau nurodytus veiksmus,

1 žingsnis: Suraskite vieną kubinės lygties sprendimą ir išbandykite metodą. Tarkime, kad turime kubinę lygtį P(x), tada raskite bet kurią x = a, P(a) = 0, imdami x = 0, ±1, ±2, ±3, … ir pan.

2 žingsnis: Kai gauname, P(a) = 0, raskime P(x) koeficientą (x – a)

3 veiksmas: Padalinkite P(x) iš (x – a), kad gautumėte kvadratinę lygtį, tarkime Q(x) naudodami polinominį padalijimą.

4 veiksmas: Faktarizuokite kvadratinę lygtį Q(x), kad gautumėte veiksnius kaip (x – b) ir (x – c).

5 veiksmas: (x – a), (x – b) ir (x – c) yra P(x) faktoriai ir išsprendę kiekvieną veiksnį gauname lygties kaip, a, b ir c šaknis.

Išmokti daugiau apie, Dalijamasis polinomas

Kubinių lygčių sprendimas

A Kubinė lygtis galima išspręsti dviem būdais

• Sumažinant ją į kvadratinę lygtį ir tada išspręsdami faktoringo arba kvadratine formule
• Grafiniu metodu

A Kubinė lygtis turi tris šaknis. Šios šaknys gali būti tikros arba įsivaizduojamos. Be to, gali būti skirtingos šaknys arba dvi tos pačios ir viena skirtinga šaknis ir visos trys tos pačios šaknys.

Pažymėtina, kad bet kuriai lygčiai, įskaitant Kubinės lygtys , lygtis visada turi būti išdėstyta standartine forma prieš sprendžiant lygtį.

Pavyzdžiui, jei duota lygtis yra 2x²-5 = x + 4/x, tada turime iš naujo išdėstyti tai į standartinę formą, ty 2x³-x²-5x-4 = 0. Dabar lygtį galime išspręsti naudodami bet kurį tinkamą metodą.

Kubinių lygčių sprendimas naudojant veiksnius

Kubinės lygties sprendimas naudojant faktorių teoremą paaiškinamas naudojant toliau pateiktą pavyzdį,

Pavyzdys: Raskite lygties f(x) = 3x šaknis ³ -16 kartų ² + 23x − 6 = 0.

Sprendimas:

Duota išraiška: f(x) = 3x³-16 kartų²+ 23x − 6 = 0

Pirmiausia padalykite daugianarį faktorių, kad gautumėte šaknis

Kadangi konstanta yra -6, galimi veiksniai yra 1, 2, 3, 6

f(1) = 3 – 16 + 23 – 6 ≠ 0

f(2) = 24 – 64 + 46 – 6 = 0

f(3) = 81 – 144 + 69 – 6 = 0

f(6) = 648 – 576 + 138 – 6 ≠ 0

Mes tai žinome, anot Faktoriaus teorema jei f(a) = 0, tai (x-a) yra f(x) koeficientas

Taigi (x – 2) ir (x – 3) yra f(x) koeficientai. Todėl (x – 2) ir (x – 3) sandauga taip pat bus f(x) koeficientas. Dabar norėdami rasti likusius veiksnius, naudokite ilgojo padalijimo metodą ir padalykite f(x) iš (x – 2) ir (x – 3) sandaugos.

Vadinasi, daliklis = (x – 2) (x – 3) = (x²– 5x + 6) ir Dividendas = 3x³-16 kartų²+ 23x − 6. Dabar padalinkite, kaip parodyta žemiau,

Po padalijimo gauname (3x-1) kaip koeficientą, o liekana yra 0. Dabar kaip Padalijimo algoritmas Mes tai žinome Dividendas = daliklis × dalinys + likutis.

⇒ f(x) = (3x³-16 kartų²+ 23x − 6) = (x²– 5x + 6) (3x-1)

Kadangi f(x) = 0

⇒ (x²– 5x + 6) (3x-1) = 0

⇒ x²– 5x + 6 = 0 arba 3x-1 = 0

Dabar imsime 3x-1 = 0 ⇒ x = 1/3, nes jau žinome dvi šaknis iš x²– 5x + 6, kurie yra 2 ir 3

Taigi,

Duotosios šaknys Kubinė lygtis yra 1/3, 2 ir 3.

Kubinių lygčių sprendimas grafiniu metodu

Kubinė lygtis išsprendžiama grafiškai, kai negalite išspręsti pateiktos lygties kitais būdais. Taigi, mums reikia tikslaus nurodytos kubinės lygties brėžinio. Lygties šaknys yra taškas (-iai), kuriame grafikas kerta X ašį, jei lygtis yra x, o jei lygtis yra y, tada lygties šaknys yra taškai, kuriuose grafikas nupjauna Y ašį.

arp – komanda

Kubinės lygties realiųjų sprendinių skaičius yra lygus skaičiui, kiek kartų kubinės lygties grafikas kerta X ašį.

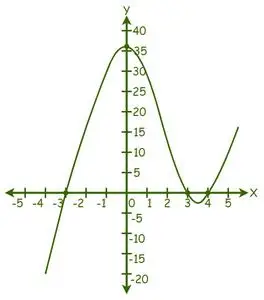
Pavyzdys: Raskite lygties f(x) = x šaknis ³ – 4x ² − 9x + 36 = 0, naudojant grafinį metodą.

Sprendimas:

Duota išraiška: f(x) = x³– 4x²− 9x + 36 = 0.

Dabar tiesiog pakeiskite atsitiktines x reikšmes nurodytos funkcijos diagramoje:

x	-4	-3	-2	-1	0	1	2	3	4	5
f(x)	-56	0	19	40	36	24	10	0	0	16

Matome, kad grafikas nupjovė X ašį 3 taškais, todėl yra 3 realūs sprendiniai.

Grafike pateikiami sprendiniai: x = -3, x = 3 ir x = 4.

Taigi pateiktos lygties šaknys yra -3, 3 ir 4.

Skaityti daugiau,

• Tiesinė lygtis
• Kvadratinės lygties sprendimas
• Faktoringo polinomai

Kubinių lygčių sprendimo uždaviniai

1 uždavinys: Raskite f(x) = x šaknis ³ – 4x ² -3x + 6 = 0.

Sprendimas:

Duota išraiška: f(x) = x³– 4x²-3x + 6 = 0.

Pirmiausia padalykite daugianarį faktorių, kad gautumėte šaknis.

Kadangi konstanta yra +6, galimi koeficientai yra 1, 2, 3, 6.

f(1) = 1 – 4 – 3 + 6 = 7 – 7 = 0

f(2) = 8 – 16 – 6 + 6 ≠ 0

f(3) = 27 – 36 – 9 + 6 ≠ 0

f(6) = 216 - 144 -18 + 6 = -48 ≠ 0

Taigi, pasak Faktoriaus teorema (x – 1) yra duotosios lygties koeficientas. Dabar norėdami rasti likusius veiksnius, naudokite ilgojo padalijimo metodą.

Pagal Padalijimo algoritmas galime rašyti,

Taigi, f(x) = x³– 4x²-3x + 6 = (x - 1) (x²– 3x – 6) = 0

⇒ (x – 1) = 0 arba (x²– 3x – 6) = 0

Žinome, kad kvadratinės lygties šaknys ax²+ bx + c = 0 yra,

x = [-b ± √(b²-4ac)]/2a

Taigi, už (x²– 3x – 6) = 0

x = [3 ± √(3²– 4(1)(-6)]/2(1)

x = (3 ± √33)/2

Vadinasi, pateiktos kubinės lygties šaknys yra 1, (3+√33)/2 ir (3–√33)/2.

2 uždavinys: Raskite lygties f(x) = 4x šaknis ³ – 10 kartų ² + 4x = 0.

Sprendimas:

Duota išraiška: f(x) = 4x³– 10 kartų²+ 4x = 0

⇒ x (4x²– 10x + 4) = 0

⇒ x (4x²– 8x – 2x + 4) = 0

⇒ x(4x(x – 2) – 2(x – 2)) = 0

⇒ x (4x – 2) (x – 2) = 0

⇒ x = 0 arba 4x – 2 = 0, x – 2 = 0

⇒ x = 0 arba x = 1/2 arba x = 2

Taigi pateiktos lygties šaknys yra 0, 1/2 ir 2.

3 uždavinys: Raskite lygties f(x) = x šaknis ³ + 3x ² + x + 3 = 0.

Sprendimas:

Duota išraiška: f(x) = x³+ 3x²+ x + 3 = 0.

⇒ x²(x + 3) + 1 (x + 3) = 0

⇒ (x + 3) (x²+1) = 0

⇒ x + 3 = 0 arba x²+1 = 0

⇒ x = -3, ±i

Taigi, duotoji lygtis turi tikrąją šaknį, ty -3, ir dvi įsivaizduojamas šaknis, ty ±i.

4 uždavinys: Raskite lygties f(x) = x šaknis ³ – 7x ² – x + 7 = 0.

Sprendimas:

Pateiktos išraiškos,

f(x) = x³– 3x²– 5x + 7 = 0

Pirmiausia suskaidykite lygtį f(x): x³– 3x²– 5x + 7 = 0

Jį galima apskaičiuoti į (x-7) (x+1) (x-1) = 0

Įvertinę daugianarį, galime rasti šaknis, prilygindami kiekvieną veiksnį nuliui. Pavyzdžiui:

• x – 7 = 0, taigi x = 7
• x + 1 = 0, taigi x = -1
• x – 1 = 0, taigi x = 1

Taigi lygties f(x) šaknys: x³– 3x²– 5x + 7 = 0 are

• x = 7
• x = -1
• x = 1

5 uždavinys: Raskite lygties f(x) = x šaknis ³ – 6x ² + 11x − 6 = 0, naudojant grafinį metodą.

Sprendimas:

Duota išraiška: f(x) = x³– 6x²+ 11x − 6 = 0.

Dabar tiesiog pakeiskite atsitiktines x reikšmes nurodytos funkcijos diagramoje:

x	1	2	3	4	5
f(x)	0	0	0	6	24

Matome, kad grafikas nupjovė X ašį 3 taškais, todėl yra 3 realūs sprendiniai.

Grafike pateikiami sprendiniai: x = 1, x = 2 ir x = 3.

Taigi pateiktos lygties šaknys yra 1, 2 ir 3.

Praktikos uždaviniai sprendžiant kubines lygtis

Toliau pateikiamos įvairios praktinės problemos, susijusios su kubinėmis lygtimis. Išspręskite šias problemas, kad suprastumėte, kaip išspręsti kubinę lygtį?

P1. Išspręskite kubinę lygtį, 3x³+ 2x²– 11x + 7 = 0.

kas yra android velykinis kiaušinis

P2. Raskite kubinės lygties šaknis, 4x³– 12 kartų²+ 17 = 0.

P3. Išspręskite kubinę lygtį, x³+ 4x²– x + 3 = 0 naudojant grafinį metodą.

P4. Raskite skaičių, kuris atitinka, -9x³+ 11x²– 8x + 2 = 0.

DUK apie kubinių lygčių sprendimą

1. Kas yra kubinės lygtys?

Kubinės lygtys yra algebrinės lygtys, kuriose didžiausia kintamojo galia yra 3

2. Kaip paskaičiuoti kubinę lygtį?

Kubinę lygtį galime apskaičiuoti dviem būdais. Pirmiausia paimdami tiesinę išraišką, bendrą iš pateiktos kubinės lygties, tada turėsime tiesinę ir kvadratinę išraišką kaip sandaugą. Ši kvadratinė lygtis gali būti toliau faktorinuojama, kad būtų gauti visi veiksniai. Antrasis būdas yra rasti duotosios kubinės lygties nulį, sudėjus atsitiktines reikšmes. Reikšmė, kurios lygties reikšmė bus lygi nuliui, bus vienas iš duotosios kubinės lygties nulių. Dabar, naudodamiesi faktoriaus teorema, suformuokite tiesinę išraišką, tarkime, x-a ir padalykite pateiktą kubinę lygtį iš šios išraiškos, kuri duos kvadratinę lygtį kaip koeficientą. Šią gautą kvadratinę lygtį galima dar labiau padalyti į faktorius, kad būtų gauti visi veiksniai.

3. Kaip grafiškai išsprendžiate kubinę lygtį?

Norėdami išspręsti kubinę lygtį, grafiškai įdėkite atsitiktines x reikšmes į pateiktą kubinę lygtį ir išspręskite, gausite y reikšmes. Pavaizduokite šias gautas reikšmes grafike. Raskite koordinates, kuriose grafikas kerta x ašį. Šios koordinatės yra kubinės lygties sprendimas.

4. Ar galima tiksliai išspręsti visas kubines lygtis?

Bet kuri lygtis, turinti nelyginę galią, turi turėti vieną tikrąją šaknį. Vadinasi, kubinėje lygtyje turi būti bent viena realioji šaknis, skirtingai nuo kvadratinės lygties, kai abi šaknys gali būti įsivaizduojamos, kai diskriminantas yra mažesnis už nulį.

5. Ar kubinėje lygtyje gali būti keli sprendimai?

Taip, kubinės lygtys gali turėti kelis sprendinius, nes kubinė lygtis gali turėti iki trijų skirtingų realių šaknų.

6. Ką reiškia lygties laipsnis?

Didžiausia galia, kurią turi lygties kintamasis, vadinama daugianario laipsniu.

7. Kuo skiriasi polinomas ir lygtis?

Polinomas yra tiesiog algebrinė lygtis, kurioje kintamojo galia yra neneigiamas sveikasis skaičius. Šis daugianomas, kai prilyginamas (=) su skaitine verte arba kitu daugianario, tada jis vadinamas lygtimi.

8. Kas yra faktoriaus teorema kubinėms lygtims?

Faktoriaus teorema teigia, kad jei r yra kubinės lygties ax šaknis (sprendinys)³+ bx²+ cx + d = 0, tada x – r yra lygties koeficientas.

9. Ką daryti, jei negaliu rasti tikslių sprendimų naudojant formules?

Jei atrodo, kad neįmanoma rasti tikslių sprendimų, galime naudoti skaitinius metodus, tokius kaip iteraciniai metodai (pvz., Niutono metodas), kad aproksimuotų lygties šaknis.

Išmokti daugiau apie Niutono Rafsono metodas .