Informatikos moksle egzistuoja kai kurios problemos, kurių sprendimai dar nerasta, problemos skirstomos į klases, žinomas kaip Sudėtingumo klasės . Sudėtingumo teorijoje sudėtingumo klasė yra susijusių sudėtingumo problemų rinkinys. Šios klasės padeda mokslininkams grupuoti problemas pagal tai, kiek laiko ir vietos jiems reikia problemoms išspręsti ir sprendimams patikrinti. Tai skaičiavimo teorijos šaka, nagrinėjanti problemai išspręsti reikalingus išteklius.
šakalas prieš vilką
Bendrieji ištekliai yra laikas ir erdvė, tai reiškia, kiek laiko algoritmui reikia problemai išspręsti ir atitinkamą atminties naudojimą.
- Algoritmo sudėtingumas laike naudojamas apibūdinti žingsnių, reikalingų problemai išspręsti, skaičių, tačiau jis taip pat gali būti naudojamas apibūdinti, kiek laiko užtrunka atsakymui patikrinti.
- Algoritmo erdvės sudėtingumas apibūdina, kiek atminties reikia algoritmui veikti.
Sudėtingumo klasės yra naudingos organizuojant panašaus pobūdžio problemas.
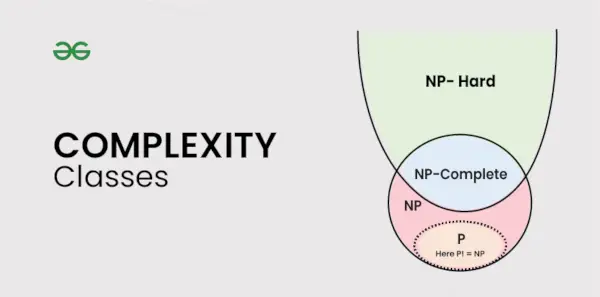
Sudėtingumo klasių tipai
Šiame straipsnyje aptariamos šios sudėtingumo klasės:
- P klasė
- NP klasė
- CoNP klasė
- NP-sunku
- NP pilnas
P klasė
P klasėje P reiškia Polinominis laikas. Tai yra sprendimų problemų rinkinys (problemos, kurių atsakymas yra taip arba ne), kurias gali išspręsti deterministinė mašina daugianario laiku.
Funkcijos:
- Sprendimas dėl P problema s lengva rasti.
- P dažnai yra skaičiavimo problemų, kurias galima išspręsti ir sekti, klasė. Tracable reiškia, kad problemas galima išspręsti tiek teoriškai, tiek praktiškai. Tačiau problemos, kurias galima išspręsti teoriškai, bet ne praktiškai, yra žinomos kaip neįveikiamos.
Šioje klasėje yra daug problemų:
- Didžiausio bendro daliklio apskaičiavimas.
- Raskite maksimalų atitikimą.
- Sujungti Rūšiuoti
NP klasė
NP NP klasėje reiškia Nedeterministinis polinominis laikas . Tai sprendimų problemų rinkinys, kurį daugianario laiku gali išspręsti nedeterministinė mašina.
Funkcijos:
- NP klasės sprendimus sunku rasti, nes juos sprendžia nedeterministinė mašina, tačiau sprendimus lengva patikrinti.
- NP uždavinius galima patikrinti Tiuringo mašina daugianario laiku.
Pavyzdys:
Panagrinėkime pavyzdį, kad geriau suprastume NP klasė . Tarkime, kad yra įmonė, turinti iš viso 1000 darbuotojai, turintys unikalų darbuotoją ID . Tarkime, kad yra 200 laisvi kambariai. Pasirinkimas iš 200 darbuotojai turi būti suporuoti kartu, tačiau įmonės vadovas turi kai kurių darbuotojų, kurie dėl asmeninių priežasčių negali dirbti vienoje patalpoje, duomenis.
Tai pavyzdys an E.G problema. Kadangi lengva patikrinti, ar pasirinktas 200 bendradarbio pasiūlytų darbuotojų skaičius yra patenkinamas arba ne, t. Tačiau sukurti tokį sąrašą nuo nulio atrodo taip sunku, kad tai visiškai nepraktiška.
Tai rodo, kad jei kas nors gali mums pateikti problemos sprendimą, galime rasti teisingą ir neteisingą porą daugianario laiku. Taigi už E.G klasės uždavinys, galimas atsakymas, kurį galima apskaičiuoti daugianario laiku.
Šioje klasėje yra daug problemų, kurias norėtųsi efektyviai išspręsti:
sujungti rūšiuoti java
- Būlio patenkinimo problema (SAT).
- Hamiltono kelio problema.
- Grafiko dažymas.
Co-NP klasė
Co-NP reiškia NP klasės papildymą. Tai reiškia, kad jei atsakymas į problemą Co-NP yra Ne, tada yra įrodymas, kurį galima patikrinti daugianario laiku.
Funkcijos:
- Jei problema X yra NP, tai jos papildinys X' taip pat yra CoNP.
- NP ir CoNP problemai nereikia tikrinti visų atsakymų vienu metu daugianario laiku, reikia patikrinti tik vieną konkretų atsakymą taip arba ne daugianario laiku, kad problema būtų NP arba CoNP.
Kai kurie CoNP problemų pavyzdžiai:
java patikrinimas yra niekinis
- Norėdami patikrinti pirminį skaičių.
- Sveikųjų skaičių faktorizavimas.
NP-kieta klasė
Sunki NP problema yra bent tokia pat sudėtinga, kaip ir sunkiausia NP problema, ir tai yra problemų klasė, dėl kurios kiekviena NP problema redukuojama į NP sudėtingą.
Funkcijos:
- Visos NP sunkios problemos nėra NP.
- Norint juos patikrinti, reikia daug laiko. Tai reiškia, kad jei pateikiamas sudėtingos NP problemos sprendimas, užtrunka ilgai, kol patikrinama, ar jis teisingas, ar ne.
- Užduotis A yra sudėtinga NP, jei kiekvienai NP problemai L yra daugianario laiko redukcija nuo L iki A.
Kai kurie Np-hard problemų pavyzdžiai yra šie:
- Sustabdymo problema.
- Kvalifikuotos Būlio formulės.
- Nėra Hamiltono ciklo.
NP-pilna klasė
Problema yra NP baigta, jei ji yra ir NP, ir NP sudėtinga. Užbaigtos NP problemos yra sudėtingiausios NP problemos.
Funkcijos:
- Užbaigtos NP problemos yra ypatingos, nes bet kuri NP klasės problema gali būti transformuota arba sumažinta į NP užbaigtas problemas daugianario laiku.
- Jei būtų galima išspręsti NP pilną uždavinį daugianario laiku, tai taip pat būtų galima išspręsti bet kurią NP problemą daugianario laiku.
Keletas problemų pavyzdžių:
- Hamiltono ciklas.
- Pasitenkinamumas.
- Viršūnės dangtelis .
| Sudėtingumo klasė | Būdingas bruožas |
| P | Lengvai išsprendžiamas daugianario laiku. |
| E.G | Taip, atsakymus galima patikrinti daugianario laiku. |
| Co-NP | Ne, atsakymus galima patikrinti daugianario laiku. |
| NP-sunku | Visų NP sudėtingų problemų nėra NP ir jas patikrinti reikia ilgai. |
| NP pilnas | Problema, kuri yra NP ir NP sudėtinga, yra NP baigta. |
