Tiesinė regresija ir Logistinė regresija yra du garsūs mašininio mokymosi algoritmai, kuriems taikoma prižiūrima mokymosi technika. Kadangi abu algoritmai yra prižiūrimo pobūdžio, šie algoritmai prognozėms naudoja pažymėtą duomenų rinkinį. Tačiau pagrindinis skirtumas tarp jų yra tai, kaip jie naudojami. Linijinė regresija naudojama regresijos problemoms spręsti, o logistinė regresija naudojama klasifikavimo problemoms spręsti. Abiejų algoritmų aprašymas pateikiamas toliau kartu su skirtumų lentele.
Tiesinė regresija:
- Tiesinė regresija yra vienas iš paprasčiausių mašininio mokymosi algoritmų, kuris patenka į prižiūrimo mokymosi techniką ir naudojamas regresijos problemoms spręsti.
- Jis naudojamas nenutrūkstamam priklausomam kintamajam prognozuoti naudojant nepriklausomus kintamuosius.
- Tiesinės regresijos tikslas yra rasti geriausiai tinkančią liniją, kuri gali tiksliai numatyti nuolatinio priklausomo kintamojo išvestį.
- Jei prognozavimui naudojamas vienas nepriklausomas kintamasis, jis vadinamas paprasta tiesine regresija, o jei yra daugiau nei du nepriklausomi kintamieji, tokia regresija vadinama daugialype tiesine regresija.
- Surasdamas geriausiai tinkančią liniją, algoritmas nustato ryšį tarp priklausomo kintamojo ir nepriklausomo kintamojo. Ir santykiai turėtų būti linijinio pobūdžio.
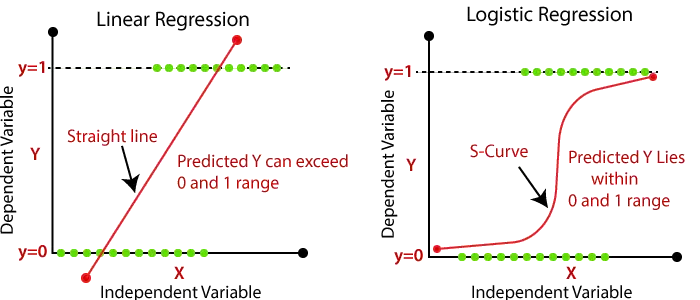
- Tiesinės regresijos išvestis turėtų būti tik tolydžios reikšmės, tokios kaip kaina, amžius, atlyginimas ir kt. Ryšys tarp priklausomo kintamojo ir nepriklausomo kintamojo gali būti parodytas toliau pateiktame paveikslėlyje:

Aukščiau pateiktame paveikslėlyje priklausomas kintamasis yra Y ašyje (atlyginimas), o nepriklausomas kintamasis yra x ašyje (patirtis). Regresijos liniją galima parašyti taip:
y= a<sub>0</sub>+a<sub>1</sub>x+ ε
Kur0ir a1yra koeficientai, o ε yra paklaidos narys.
Logistinė regresija:
- Logistinė regresija yra vienas iš populiariausių mašininio mokymosi algoritmų, patenkančių į prižiūrimo mokymosi metodus.
- Jis gali būti naudojamas klasifikavimo ir regresijos problemoms spręsti, tačiau daugiausia naudojamas klasifikavimo problemoms spręsti.
- Logistinė regresija naudojama kategoriškai priklausomam kintamajam prognozuoti nepriklausomų kintamųjų pagalba.
- Logistinės regresijos problemos rezultatas gali būti tik nuo 0 iki 1.
- Logistinė regresija gali būti naudojama, kai reikia dviejų klasių tikimybės. Pavyzdžiui, ar šiandien lis lietus, ar ne, 0 arba 1, tiesa ar klaidinga ir tt
- Logistinė regresija pagrįsta didžiausios tikimybės įvertinimo koncepcija. Pagal šį įvertinimą stebimi duomenys turėtų būti labiausiai tikėtini.
- Logistinės regresijos metu svertinę įvesties sumą perduodame per aktyvinimo funkciją, kuri gali susieti reikšmes tarp 0 ir 1. Tokia aktyvinimo funkcija vadinama sigmoidinė funkcija ir gauta kreivė vadinama sigmoidine kreive arba S kreive. Apsvarstykite toliau pateiktą vaizdą:

- Logistinės regresijos lygtis yra tokia:

Skirtumas tarp tiesinės regresijos ir logistinės regresijos:
| Tiesinė regresija | Logistinė regresija |
|---|---|
| Tiesinė regresija naudojama nenutrūkstamam priklausomam kintamajam prognozuoti naudojant tam tikrą nepriklausomų kintamųjų rinkinį. | Logistinė regresija naudojama kategoriškai priklausomam kintamajam numatyti naudojant tam tikrą nepriklausomų kintamųjų rinkinį. |
| Tiesinė regresija naudojama regresijos uždaviniui spręsti. | Klasifikavimo uždaviniams spręsti naudojama logistinė regresija. |
| Taikant tiesinę regresiją, mes prognozuojame nuolatinių kintamųjų reikšmę. | Logistinėje regresijoje mes prognozuojame kategorinių kintamųjų reikšmes. |
| Taikant tiesinę regresiją, randame geriausiai tinkančią liniją, pagal kurią galime lengvai numatyti išvestį. | Logistinėje regresijoje randame S kreivę, pagal kurią galime klasifikuoti pavyzdžius. |
| Tikslumui įvertinti naudojamas mažiausio kvadrato įvertinimo metodas. | Tikslumui įvertinti naudojamas didžiausios tikimybės įvertinimo metodas. |
| Tiesinės regresijos išvestis turi būti nuolatinė vertė, pvz., kaina, amžius ir kt. | Logistinės regresijos išvestis turi būti kategorinė reikšmė, pvz., 0 arba 1, Taip arba Ne ir kt. |
| Taikant tiesinę regresiją, priklausomo kintamojo ir nepriklausomo kintamojo ryšys turi būti tiesinis. | Logistinėje regresijoje nebūtina turėti tiesinio ryšio tarp priklausomo ir nepriklausomo kintamojo. |
| Taikant tiesinę regresiją, tarp nepriklausomų kintamųjų gali būti kolineariškumas. | Logistinėje regresijoje nepriklausomo kintamojo neturėtų būti kolineariškumo. |
