Inercijos momentas yra kūno savybė besisukančio judėjimo metu. Inercijos momentas yra besisukančių kūnų savybė, linkusi prieštarauti kūno sukamojo judėjimo pokyčiams. Jis panašus į bet kurio kūno inerciją transliacinio judėjimo metu. Matematiškai inercijos momentas pateikiamas kaip kiekvienos dalelės masės ir atstumo nuo sukimosi ašies kvadrato sandaugos suma. Jis matuojamas vienetais kgm 2 .
Išsamiau apie inercijos momentą sužinokime toliau pateiktame straipsnyje.
Turinys
- Inercijos momento apibrėžimas
- Inercijos formulės momentas
- Veiksniai, turintys įtakos inercijos momentui
- Kaip apskaičiuoti inercijos momentą?
- Inercijos momento formulė įvairioms formoms
- Giriacijos spindulys
- Inercijos momento teoremos
- Inercijos momentai skirtingiems objektams
Inercijos momento apibrėžimas
Inercijos momentas yra kūno polinkis sukantis, prieštaraujantis jo pokyčiams sukamasis judesys dėl išorinių jėgų. Inercijos momentas elgiasi kaip kampinė masė ir vadinama sukimosi inercija. Inercijos momentas yra analogiškas mechaniniam Inercija kūno.
MOI apibrėžiamas kaip kiekis, išreikštas produkto suma masė kiekvienos dalelės atstumo nuo sukimosi ašies kvadratu.
Inercijos momento vienetas
Inercijos momentas yra skaliarinis dydis, o inercijos momento SI vienetas yra kgm 2 .
Inercijos momento matmenų formulė
Kadangi inercijos momentas pateikiamas kaip masės ir atstumo kvadrato sandauga. Jo matmenų formulė gaunamas masės matmenų formulės ir ilgio matmenų formulės kvadrato sandauga. Inercijos momento matmenų formulė yra ML 2
Kas yra Inercija?
Inercija yra materijos savybė, dėl kurios ji linkusi priešintis savo judėjimo būsenos pokyčiams. Tai reiškia, kad ramybės būsenoje esantis kūnas bando išlikti ramybėje ir atsispirti bet kokiai jėgai, bandančia jį pajudinti, o judantis kūnas bando tęsti judėjimą ir atsispirti bet kokiai jėgai, bandančia jį priversti pakeisti jo judėjimo mastą. Pagal kiekį jis yra lygus didžiausiai jėgai, bandančiai pakeisti savo būseną judesį .
Išmokti daugiau apie Inercija .
Inercijos formulės momentas
Inercijos momentas yra a skaliarinis dydis . Matematiškai dalelės masės ir atstumo nuo sukimosi ašies kvadrato sandauga vadinama dalelės inercijos apie sukimosi ašį momentu.
Bendra bet kurio objekto inercijos momento nustatymo formulė yra tokia:
aš = p 2
kur,
m yra objekto masė'
r yra atstumas nuo sukimosi ašies
Kūnui, sudarytam iš ištisinių be galo mažų dalelių, inercijos momentui apskaičiuoti naudojama integralioji inercijos momento forma.
I = ∫dI
aš =
int_{0}^{M} r^2 dm
Dalelių sistemos inercijos momentas
Dalelių sistemos inercijos momentas apskaičiuojamas pagal formulę,
I = ∑m i r i 2
kur,
r i yra statmenas atstumas nuo ithdalelė nuo ašies
m i yra i masėthdalelė
Aukščiau pateikta inercijos momento lygtis rodo, kad dalelių sistemos inercijos momentas yra lygus kiekvienos dalelės masės sandaugai ir atstumo nuo kiekvienos dalelės sukimosi ašies kvadrato.
Žemiau pateiktam paveikslui
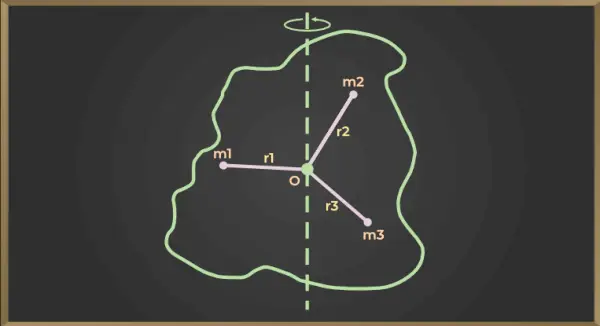
Pirmosios dalelės inercijos momentas = m1×r12
Antrosios dalelės inercijos momentas = m2×r22
Trečiosios dalelės inercijos momentas = m3×r32
Panašiai,
n inercijos momentasthdalelė = mn×rn2
Dabar viso kūno inercijos momentas apie sukimosi ašį AB bus lygus visų dalelių inercijos momentų sumai, taigi
aš = m1×r12+ m2×r22+ m3×r32+……+mn×rn2
yra java metodas
I = Σm i ×r i 2
kur,
aš reiškia kūno inercijos momentą apie sukimosi ašį
m i yra i masėthdalelė,
r i yra i spindulysthdalelė
S reiškia sumą.
Iš lygties galime pasakyti, kad kūno inercijos momentas apie fiksuotą ašį yra lygus kiekvienos to kūno dalelės masės sandaugos ir jos statmeno atstumo nuo fiksuotos ašies kvadrato sumai.
Veiksniai, turintys įtakos inercijos momentui
Bet kurio objekto inercijos momentas priklauso nuo šių reikšmių:
- Objekto forma ir dydis
- Objekto medžiagos tankis
- Sukimosi ašis
Kaip apskaičiuoti inercijos momentą?
Įpratę keli būdai apskaičiuokite inercijos momentą bet kokio besisukančio objekto.
- Vienodiems objektams inercijos momentas apskaičiuojamas imant masės sandaugą su atstumo nuo sukimosi ašies kvadratu (r2).
- Nevienodiems objektams apskaičiuojame inercijos momentą, paimdami atskirų taškinių masių sandaugą kiekviename skirtingame spinduliu, tam naudojama formulė:
I = ∑m i r i 2
Inercijos momento formulė įvairioms formoms
Šioje lentelėje aptariamos kai kurių simetriškų objektų inercijos momento išraiškos kartu su jų sukimosi ašimi:

| Objektas | Ašis | Inercijos momento išraiška |
|---|---|---|
| Tuščiaviduris cilindras Plonasienis | Centrinis | Aš = p2 |
| Plonas žiedas | Skersmuo | I = 1/2 p2 |
| Žiedinis žiedas arba tuščiaviduris cilindras | Centrinis | I = 1/2 M(r22+ r12) |
| Tvirtas cilindras | Centrinis | I = 1/2 p2 |
| Vienodas diskas | Skersmuo | I = 1/4 p2 |
| Tuščiavidurė sfera | Centrinis | I = 2/3 p2 |
| Tvirta sfera | Centrinis | I = 2/5 p2 |
| Vienodas simetriškas sferinis apvalkalas | Centrinis | |
| Vienoda plokštelė arba stačiakampis lygiagretus vamzdis | Centrinis | I = 1/12 M(a2+ b2) |
| Plonas strypas | Centrinis | I = 1/12 p2 |
| Plonas strypas | Strypo gale | I = 1/3 p2 |
Giriacijos spindulys
The Giriacijos spindulys kūno apibrėžiamas kaip statmenas atstumas nuo sukimosi ašies iki masės taško, kurio masė yra lygi viso kūno masei, o inercijos momentas yra lygus tikrajam objekto inercijos momentui. daroma prielaida, kad ten sutelkta visa kūno masė. Tai įsivaizduojamas atstumas. Giriacijos spindulys žymimas K.
Jei kūno masė ir sukimosi spindulys yra atitinkamai M ir K, tai kūno inercijos momentas yra
I = MK 2 ……(1)
Taigi kūno sukimosi spindulys yra statmenas sukimosi ašiai, kurios kvadratas, padaugintas iš to kūno masės, suteikia to kūno inercijos momentą apie tą ašį.
Vėlgi pagal (1) lygtį K2= I/M
K = √ (I/m)
Taigi kūno sukimosi apie ašį spindulys yra lygus kūno santykio aplink tą ašį kvadratinei šaknei.
Inercijos momento teoremos
Yra dviejų tipų teoremos, kurios yra labai svarbios inercijos momentui:
- Lygiagrečios ašies teorema
- Statmenos ašies teorema
Statmenos ašies teorema
Statmenos ašies teorema teigia, kad kūno inercijos momento apie dvi viena kitai statmenas ašis, esančias kūno plokštumoje, suma yra lygi kūno inercijos momentui apie trečią ašį, kuri yra statmena abiem ašims ir eina per jų tašką sankryžos.

Aukščiau pateiktame paveikslėlyje JAUTIS ir LTD yra dvi ašys kūno plokštumoje, kurios yra statmenos viena kitai. Trečioji ašis yra OZ kuri yra statmena kūno plokštumai ir eina per susikirtimo tašką JAUTIS ir LTD kirvius. Jeigu aš x , aš ir , ir aš Su yra kūno inercijos apie ašį momentai JAUTIS , LTD , ir OZ ašys atitinkamai, tada pagal šią teoremą
aš x + aš ir = aš Su
Lygiagrečios ašies teorema
Pagal Lygiagrečios ašies teorema , kūno inercijos momentas apie tam tikrą ašį yra inercijos momento apie ašį, einančią per to kūno masės centrą, ir kūno masės kvadrato ir statmeno atstumo tarp dvi ašys.
java concat eilutės

Tegul aukščiau pateiktame paveikslėlyje turime rasti inercijos momentą aš O kūno, einančio per tašką O ir apie ašį, statmeną plokštumai, o kūno inercijos momentas, einantis per masės centrą C o apie ašį, lygiagrečią duotai ašiai, yra aš C , tada pagal šią teoremą
aš O = aš C + ml 2
kur
M yra viso kūno masė
l yra statmenas atstumas tarp dviejų ašių.
Inercijos momentai skirtingiems objektams
Toliau šiame straipsnyje aptariamas skirtingų objektų inercijos momentas
Stačiakampės plokštės inercijos momentas
Jei plokštės masė yra M, ilgis l ir plotis b, tai inercijos momentas eina per svorio centrą ir apie ašį, statmeną plokštės plokštumai.

I = M(l 2 + b 2 / 12)
Disko inercijos momentas
Jei disko masė M ir spindulys r, tai inercijos momentas apie disko geometrinę ašį yra

I = 1/2 (p 2 )
Strypo inercijos momentas
Jei strypo masė yra M, o ilgis yra l, tai inercijos momentas apie ašį, statmeną strypo ilgiui ir einanti per jo svorio centrą

I = ML 2 /12
Apskritimo inercijos momentas
Jei žiedo masė yra M, o žiedo spindulys yra r, tai inercijos momentas apie ašį, einančią statmenai žiedo centrui

Aš = p 2
Rutulio inercijos momentas
Jei kietosios sferos masė yra M, o spindulys r, tai jo skersmens inercijos momentas yra

I = 2/5 p 2
Kieto cilindro inercijos momentas
Kietojo cilindro, kurio spindulys „R“ ir masė M, inercijos momentas pateikiamas pagal

I = 1/2MR 2
Tuščiavidurio cilindro inercijos momentas
Tuščiaviduris cilindras turi du spindulius, būtent vidinį spindulį ir išorinį spindulį. Tuščiavidurio cilindro, kurio masė M, išorinis spindulys R, inercijos momentas1ir vidinis spindulys R2pateikiamas kaip

I = 1/2M (R 1 2 + R 2 2 )
Kietojo rutulio inercijos momentas
Masės „M“ ir spindulio „R“ kietosios sferos inercijos momentas pateikiamas kaip

I = 2/5MR 2
Tuščiavidurės sferos inercijos momentas
Tuščiavidurio rutulio, kurio masė M ir spindulys „R“, inercijos momentas pateikiamas kaip

I = 2/3MR 2
Žiedo inercijos momentas
Žiedo inercijos momentas nurodomas dviem atvejais, kai sukimosi ašis eina per centrą ir kai sukimosi ašis eina per skersmenį.
Žiedo inercijos momentas apie ašį, einantį per centrą, yra nurodytas
konvertuoti eilutę į int

I = MR 2
Žiedo inercijos momentas apie ašį, einantį per skersmenį, yra nurodytas

aš = p 2 /2
Aikštės inercijos momentas
Kraštinės „a“ kvadrato inercijos momentas pateikiamas kaip

I = a 4 /12
Kvadratinės plokštės, kurios kraštinės ilgis „l“ ir masė M, inercijos momentas pateikiamas kaip
I = 1/6 ml 2
Trikampio inercijos momentas
Trikampio inercijos momentas pateikiamas 3 situacijoms: pirma, kai ašis eina per centrą, antra, kai ašis kerta pagrindą ir trečia, kai ašis statmena pagrindui. Pažiūrėkime po vieną jų formulę. Trikampio, kurio pagrindas yra „b“ ir aukštis „h“, inercijos momento formulė pateikiama taip

Kai ašis praeina per centrinį
I = bh 3 /36
Kai ašis eina per pagrindą
I = bh 3 /12
Kai ašis yra statmena pagrindui
I = (hb/36) (b 2 – b 1 b + b 1 2 )
Skirtumas tarp inercijos momento ir inercijos
Skirtumas tarp inercijos ir inercijos momento pateiktas žemiau:
| Taip ne. | Inercija | Inercijos momentas |
|---|---|---|
| 1. | Jo svarba yra linijiniame judėjime. | Jo svarba yra sukimosi judesyje. |
| 2. | Tai ta objekto savybė, kuri prieštarauja objekto būsenos pokyčiams tiesiniu judėjimu. | Inercijos momentas yra ta objekto savybė, kuri prieštarauja objekto būsenos pasikeitimui sukimosi judesyje. |
| 3. | Objekto inercija priklauso tik nuo jo masės. | Objekto inercijos momentas priklauso nuo jo masės ir masės pasiskirstymo sukimosi ašies atžvilgiu. |
| 4. | Objekto inercija yra fiksuota. | Objekto inercijos momentas skiriasi priklausomai nuo skirtingų sukimosi ašių. |
Besisukančio kūno kinetinė energija
Tarkime, kad „m“ masės kūnas sukasi greičiu v atstumu „r“ nuo sukimosi ašies. Tada jo kampinis greitis yra ω = v/r, tada v = rω. Dabar mes žinome, kad Kinetinė energija kūno suteikia
KE = 1/2mv 2
⇒ KE = 1/2 m (rω)2
⇒ KE = 1/2mr2Oi2
⇒ KE = 1/2Iω 2
Taigi, besisukančio kūno kinetinė energija gaunama iš pusės inercijos momento sandaugos ir kampinis greitis kūno. Besisukančio kūno kinetinė energija taip pat vadinama Sukimosi kinetinė energija . Sukimosi kinetinės energijos formulė pateikta kaip
KE = 1/2Iω 2
Inercijos momentas(I) nepriklauso nuo kūno kampinio greičio. Tai yra besisukančio kūno masės ir kūno atstumo nuo sukimosi ašies funkcija. Taigi mes pastebime, kad kampinis judėjimas yra analogiškas tiesiniam judėjimui, o tai reiškia, kad inercijos momento reikšmė yra ta, kad jis suteikia idėją apie tai, kaip masės besisukančiame kūne pasiskirsto skirtingais atstumais nuo sukimosi ašies.
Inercijos momento taikymas
Inercijos momentas turi įvairių pritaikymų, kai kurie iš jų aptariami toliau:
- Dėl didesnio inercijos momento žemė sukasi aplink savo ašį tokiu pat kampiniu greičiu.
- Po vaikų žaidimo varikliu padėtas mažas judantis ratas. Įtrynus šį ratą žeme ir palikus variklį, dėl rato inercijos momento variklis kurį laiką veikia.
- Kiekvienas variklis susideda iš didelio ir sunkaus rato, pritvirtinto prie jo veleno, o didžioji masės dalis yra ant jo apskritimo. Todėl jo inercijos momentas yra didelis. Šis ratas vadinamas smagračiu. Variklio veleną varantis sukimo momentas nuolat didėja. Todėl veleno sukimasis gali būti nevienodas, tačiau dėl judančio rato, turinčio didesnę inerciją, velenas ir toliau sukasi beveik vienodu greičiu.
- Jaučių vežimų, rikšų, motorolerių, dviračių ir kt. ratuose didžioji masės dalis sutelkta ant jo apskritimo arba ratlankio. šis lankelis arba rutina yra pritvirtinta prie rato ašies standžiais stipinais. Taip darant padidėja jo inercijos momentas. Todėl, kai važiuojant dviračiu kojos nustoja judėti, ratas kurį laiką toliau sukasi.
Taip pat patikrinkite
- Sukamojo judesio kinematika
- Kieto kūno judėjimas
- Rolling Motion
Išspręsti inercijos momentų pavyzdžiai
1 pavyzdys: 500 g masės kūnas sukasi apie ašį. kūno masės centro atstumas nuo sukimosi ašies yra 1,2 m. Raskite kūno inercijos momentą apie sukimosi ašį.
Sprendimas:
Atsižvelgiant į tai, kad M = 500 g = 0,5 kg, r = 1,2 m.
Akivaizdu, kad visa kūno masė gali būti laikoma jo masės centre. Tada kūno inercijos momentas apie sukimosi ašį.
aš = p2
I = 0,5 × (1,2)2
I = 0,72 kg m2
2 pavyzdys: 1,2 kg masės kūno sukimosi spindulys apie ašį, esančią 12 cm atstumu nuo masės centro, yra 13 cm. Apskaičiuokite apsisukimo spindulys ir inercijos momentas apie ašį, einantį per masės centrą.
Sprendimas:
Atsižvelgiant į tai, M = 1,0 kg, K = 13 cm, l = 12 cm, KCM=?, ašCM= ?
kaip atskleisti paslėptas programasIš lygiagrečios ašies teoremos I = ICM+ ml2
K2= KCM2+ l2
arba KCM2= K2– l2
KCM2 = (13)2– (12)2= 25
KCM= 5
Dabar, inercijos momentas ICM= MKCM2
ašCM= 1,0 × (0,05)2= 2,5 × 10-3kg m2
3 pavyzdys: 0,1 kg masės kūnas sukasi apie ašį. jei kūno masės centro atstumas nuo sukimosi ašies yra 0,5 m, tai raskite kūno inercijos momentą.
Sprendimas:
Atsižvelgiant į tai, M = 0,1 kg ir r = 0,5 m
taigi aš = p2
I = 0,1 × (0,5)2
I = 0,025 kg m2
4 pavyzdys: žiedų inercijos momentas apie ašį, einantį per jos centrą statmenai apskrito žiedo plokštumai, yra 200 gm cm 2 . Koks bus jo skersmens inercijos momentas?
Sprendimas:
Apvalaus žiedo inercijos momentas apie ašį, einantį per kitą centrą, statmeną jo plokštumai
PONAS2= 200 gm cm2
Inercijos momentas artėja prie skersmens
= 1/2 MR2
= 1/2 × 200 = 100 gm cm2
DUK apie inercijos akimirkas
Kaip apskaičiuoti inercijos momentą?
Pagrindinė formulė, leidžianti rasti bet kurio vienodo objekto inercijos momentą, yra:
aš = p 2
kur,
m yra objekto masė'
r yra atstumas nuo sukimosi ašies
Kaip apskaičiuoti pluošto inercijos momentą?
Spindulio inercijos momentas išilgai centro ir jam horizontalios ašies apskaičiuojamas pagal formulę,
I = ML 2 / 12
Nuo ko priklauso kūno inercijos momentas?
Bet kurio objekto inercijos momentas priklauso nuo toliau nurodytų veiksnių:
- Kūno masė,
- Sukimosi ašis
- Objekto forma ir dydis
Kas yra inercijos momento vienetas?
Inercijos momento vienetas yra Kgm 2
Ar inercijos momentas gali būti neigiamas?
Ne, inercijos momentas niekada negali būti neigiamas.
Kas yra masės inercijos momentas?
Masės inercijos momentas yra kūno pasipriešinimo kampinio impulso ar krypties pokyčiams matas. Taškinės masės masės inercijos momentas apskaičiuojamas taip: I = p2o dalelių sistemai masės inercijos momentas pateikiamas kaip I = Σimiri2
Kas yra srities inercijos momentas?
Ploto inercijos momentas yra 2D formos plokštumos savybė, parodanti, kaip taškai pasiskirsto savavališkos plokštumos ašies atžvilgiu. Ploto inercijos momentas taip pat žinomas kaip antrasis ploto momentas arba kvadratinis ploto momentas. Ploto inercijos momento xy plokštumoje formulė pateikiama kaip Ixy= ∫xy dxdxy = ∫xy dA
