- Mes ištyrėme strategijas, kurios gali mąstyti tiek į priekį, tiek atgal, tačiau šių dviejų krypčių derinys yra tinkamas sudėtingai ir didelei problemai išspręsti. Tokia mišri strategija leidžia iš pradžių išspręsti didžiąją problemos dalį, o tada grįžti atgal ir išspręsti mažas problemas, kurios iškyla derinant dideles problemos dalis. Tokia technika vadinama Priemonių ir tikslų analizė .
- „Means-Ends Analysis“ yra problemų sprendimo metodai, naudojami dirbtiniame intelekte, siekiant apriboti paiešką AI programose.
- Tai paieškos atgal ir pirmyn technikos mišinys.
- Pirmą kartą MEA techniką 1961 m. pristatė Allenas Newellas ir Herbertas A. Simonas savo problemų sprendimo kompiuterinėje programoje, kuri buvo pavadinta „General Problem Solver“ (GPS).
- MEA analizės procesas buvo sutelktas į skirtumo tarp esamos būsenos ir tikslo įvertinimą.
Kaip veikia priemonių ir tikslo analizė:
Priemonių analizės procesas gali būti taikomas rekursyviai problemai spręsti. Tai strategija, skirta valdyti paiešką sprendžiant problemas. Toliau pateikiami pagrindiniai žingsniai, apibūdinantys MEA technikos veikimą sprendžiant problemą.
- Pirmiausia įvertinkite skirtumą tarp pradinės būsenos ir galutinės būsenos.
- Pasirinkite įvairius operatorius, kurie gali būti taikomi kiekvienam skirtumui.
- Prie kiekvieno skirtumo taikykite operatorių, kuris sumažina skirtumą tarp dabartinės būsenos ir tikslo būsenos.
Operatoriaus tarpinių tikslų nustatymas
MEA procese nustatome skirtumus tarp dabartinės būsenos ir tikslo būsenos. Kai atsiranda šie skirtumai, galime pritaikyti operatorių skirtumams sumažinti. Tačiau kartais gali būti, kad operatorius negali būti pritaikytas esamai būsenai. Taigi sukuriame esamos būsenos, kurioje gali būti taikomas operatorius, antrinę problemą, toks atgalinio grandinės tipas, kuriame pasirenkami operatoriai, o tada nustatomi antriniai tikslai, nustatantys operatoriaus prielaidas. Operatoriaus tarpinių tikslų nustatymas .
Priemonių ir tikslų analizės algoritmas:
Paimkime dabartinę būseną kaip DABARTINĘ ir tikslo būseną kaip TIKSLĄ, tada pateikiami MEA algoritmo veiksmai.
- Pasirinkite naują operatorių O, kuris būtų taikomas esamam skirtumui, o jei tokio nėra, signalo gedimas.
- Bandykite pritaikyti operatorių O CURRENT. Padarykite dviejų būsenų aprašymą.
i) O-Start, būsena, kai tenkinamos O prielaidos.
ii) O rezultatas – būsena, kuri atsirastų, jei O būtų pritaikyta O starte. - Jeigu
(Pirma dalis<------ mea (current, o-start)< strong>
Ir
(PASKUTINĖ dalis<----- mea (o-result, goal)< strong>, yra sėkmingi, tada praneškite apie sėkmę ir grąžinkite FIRST-PART, O ir LAST-PART sujungimo rezultatą.
Aukščiau aptartas algoritmas labiau tinka paprastai problemai, o ne tinkamas sudėtingoms problemoms spręsti.
Vidutinio tikslo analizės pavyzdys:
Paimkime pavyzdį, kai žinome pradinę būseną ir tikslo būseną, kaip nurodyta toliau. Šioje užduotyje turime gauti tikslo būseną, nustatydami skirtumus tarp pradinės būsenos ir tikslo būsenos ir taikydami operatorius.
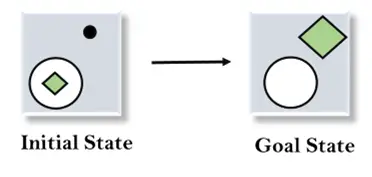
Sprendimas:
Norėdami išspręsti aukščiau pateiktą problemą, pirmiausia surasime skirtumus tarp pradinių būsenų ir tikslo būsenų, o kiekvienam skirtumui sugeneruosime naują būseną ir pritaikysime operatorius. Šios problemos operatoriai yra šie:
1. Pradinės būsenos įvertinimas: Pirmajame etape įvertinsime pradinę būseną ir palyginsime pradinę ir tikslo būseną, kad surastume skirtumus tarp abiejų būsenų.

2. Taikydami operatorių Delete: Kaip galime patikrinti, pirmasis skirtumas yra tas, kad tikslo būsenoje nėra taško simbolio, kuris būtų pradinėje būsenoje, todėl pirmiausia pritaikysime Ištrinti operatorių norėdami pašalinti šį tašką.

3. Perkėlimo operatoriaus taikymas: Pritaikius operatorių Delete, atsiranda nauja būsena, kurią vėl palyginsime su tikslo būsena. Palyginus šias būsenas, yra dar vienas skirtumas, kad kvadratas yra už apskritimo ribų, todėl taikysime Perkelti operatorių .

4. Taikant išplėtimo operatorių: Dabar trečiame žingsnyje sukuriama nauja būsena, kurią palyginsime su tikslo būsena. Palyginus būsenas išlieka vienas skirtumas – kvadrato dydis, tad taikysime Išplėsti operatorių ir galiausiai sugeneruos tikslo būseną.

