Luhn algoritmas, taip pat žinomas kaip 10 modulis arba link 10 algoritmas yra paprasta kontrolinės sumos formulė, naudojama įvairiems identifikavimo numeriams, pvz., kredito kortelių numeriams, IMEI numeriams, Kanados socialinio draudimo numeriams, patvirtinti. LUHN formulę septintojo dešimtmečio pabaigoje sukūrė matematikų grupė. Netrukus po to kredito kortelių bendrovės jį priėmė. Kadangi algoritmas yra viešas, juo gali naudotis visi. Daugumoje kredito kortelių ir daugelyje valstybinių identifikavimo numerių naudojamas algoritmas kaip paprastas būdas atskirti galiojančius numerius nuo neteisingai įvestų ar kitaip neteisingų skaičių. Jis skirtas apsaugoti nuo atsitiktinių klaidų, o ne nuo kenkėjiškų atakų.
Luhno algoritmo veiksmai
Supraskime algoritmą su pavyzdžiu:
Apsvarstykite sąskaitos numerio pavyzdį 79927398713 .
1 žingsnis – pradedant nuo dešiniojo skaitmens, padvigubinti kiekvieno antrojo skaitmens reikšmę,
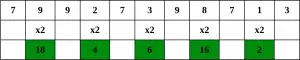
2 žingsnis – Jei padvigubėjus skaičių gaunamas dviženklis skaičius, t. y. didesnis nei 9 (pvz., 6 × 2 = 12), tada pridėkite sandaugos skaitmenis (pvz., 12: 1 + 2 = 3, 15: 1 + 5 = 6), kad gautumėte vienženklį skaičių.

3 veiksmas – Dabar paimkite visų skaičių sumą.
css paryškintas tekstas

4 veiksmas – Jei bendras modulis 10 yra lygus 0 (jei suma baigiasi nuliu), tada skaičius galioja pagal Luhno formulę; kitaip jis negalioja.

Kadangi suma yra 70, kuri yra 10 kartotinė, sąskaitos numeris gali būti tinkamas.
Idėja paprasta; tranzuojame nuo galo. Prieš pridėdami kiekvieną antrą skaitmenį, jį padvigubiname. Sudedame du skaitmenis, gautus padvigubėjus.
Įgyvendinimas:
C++
// C++ program to implement Luhn algorithm> #include> using> namespace> std;> // Returns true if given card number is valid> bool> checkLuhn(>const> string& cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum = 0, isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; i--) {> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits after> >// doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> // Driver code> int> main()> {> >string cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >printf>(>'This is a valid card'>);> >else> >printf>(>'This is not a valid card'>);> >return> 0;> }> |
>
>
Java
// Java program to implement> // Luhn algorithm> import> java.io.*;> class> GFG {> > // Returns true if given> // card number is valid> static> boolean> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum =>0>;> >boolean> isSecond =>false>;> >for> (>int> i = nDigits ->1>; i>=>0>; i--)> >{> >int> d = cardNo.charAt(i) ->'0'>;> >if> (isSecond ==>true>)> >d = d *>2>;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d />10>;> >nSum += d %>10>;> >isSecond = !isSecond;> >}> >return> (nSum %>10> ==>0>);> }> >// Driver code> >static> public> void> main (String[] args)> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >System.out.println(>'This is a valid card'>);> >else> >System.out.println(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
java sąrašo eilutė
>
>
Python3
# Python3 program to implement> # Luhn algorithm> # Returns true if given card> # number is valid> def> checkLuhn(cardNo):> > >nDigits>=> len>(cardNo)> >nSum>=> 0> >isSecond>=> False> > >for> i>in> range>(nDigits>-> 1>,>->1>,>->1>):> >d>=> ord>(cardNo[i])>-> ord>(>'0'>)> > >if> (isSecond>=>=> True>):> >d>=> d>*> 2> > ># We add two digits to handle> ># cases that make two digits after> ># doubling> >nSum>+>=> d>/>/> 10> >nSum>+>=> d>%> 10> > >isSecond>=> not> isSecond> > >if> (nSum>%> 10> =>=> 0>):> >return> True> >else>:> >return> False> # Driver code> if> __name__>=>=>'__main__'>:> > >cardNo>=> '79927398713'> > >if> (checkLuhn(cardNo)):> >print>(>'This is a valid card'>)> >else>:> >print>(>'This is not a valid card'>)> # This code is contributed by rutvik_56> |
>
javascript eilutės pakeitimas
>
C#
// C# program to implement> // Luhn algorithm> using> System;> class> GFG {> > // Returns true if given> // card number is valid> static> bool> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.Length;> >int> nSum = 0;> >bool> isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; i--)>> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> >// Driver code> >static> public> void> Main()> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >Console.WriteLine(>'This is a valid card'>);> >else> >Console.WriteLine(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
java rinkinys
>
>
Javascript
> >// Javascript program to implement Luhn algorithm> > >// Returns true if given> >// card number is valid> >function> checkLuhn(cardNo)> >{> >let nDigits = cardNo.length;> >let nSum = 0;> >let isSecond =>false>;> >for> (let i = nDigits - 1; i>= 0; i--)> >{> >let d = cardNo[i].charCodeAt() ->'0'>.charCodeAt();> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += parseInt(d / 10, 10);> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> >}> > >let cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >document.write(>'This is a valid card'>);> >else> >document.write(>'This is not a valid card'>);> > > |
>
>Išvestis
This is a valid card>
Luhno algoritmas aptinka bet kokią vienaženklę klaidą, taip pat beveik visus gretimų skaitmenų perkėlimus.
