KOTANGENTO FORMULĖ

Trigonometrija yra svarbi matematikos šaka, nagrinėjanti ryšį tarp stačiakampio trikampio kraštinių ilgių ir kampų. Sinusas, kosinusas, liestinė, kosekantas, sekantas ir kotangentas yra šeši trigonometriniai santykiai arba funkcijos. Kur trigonometrinis santykis pavaizduotas kaip santykis tarp stačiakampio trikampio kraštinių.

sin θ = priešinga pusė/hipotenuzė
cos θ = gretima pusė/hipotenuzė
tan θ = priešinga pusė/gretima pusė
cosec θ = 1/sin θ = hipotenuzė / priešinga pusė
sek θ = 1/cos θ = hipotenuzė/gretima pusė
lovelė θ = 1/tan θ = gretima pusė/priešinga pusė

Kotangentinė funkcija yra duotosios liestinės funkcijos abipusė funkcija. Stačiakampio trikampio kotangentinio kampo reikšmė yra kraštinės, esančios greta nurodyto kampo, ilgio ir priešingos tam kampui kraštinės ilgio. Kotangentinę funkciją rašome kaip cot.

Trikampis ABC

Dabar kampo θ kotangentinė formulė yra

lovelė θ = (gretima pusė) / (priešinga pusė)

Kotangento funkcija yra teigiama pirmame ir trečiame kvadrantuose, o neigiama antrajame ir ketvirtame kvadrantuose.

lovelė (2π + θ) = vaikiška lovelė θ (1^Švkvadrantas)
vaikiška lovelė (π – θ) = – lovelė θ (2^ndkvadrantas)
lovelė (π + θ) = vaikiška lovelė θ (3^rdkvadrantas)
vaikiška lovelė (2π – θ) = – lovelė θ (4^thkvadrantas)

Kotangento funkcija yra neigiama funkcija, nes neigiamo kampo kotangentas yra neigiamas kotangento teigiamo kampo.

vaikiška lovelė (-θ) = – lovelė θ

Kalbant apie liestinės funkciją, kotangentinė funkcija parašyta taip,

vaikiška lovelė θ = 1/tan θ

(arba)

lova θ = įdegis (90° – θ) (arba) įdegis (π/2 – θ)

Kotangentinė funkcija sinuso ir kosinuso atžvilgiu gali būti parašyta taip,

cot θ = cos θ/sin θ

Mes žinome, kad lovelė θ = gretimoje pusėje / priešingoje pusėje

Dabar padalinkite skaitiklį ir vardiklį su hipotenuze

⇒ lovelė θ = (gretima pusė/hipotenūza) / (priešinga pusė/hipotenuzė)

Mes žinome, kad sin θ = priešinga pusė / hipotenuzė

cos θ = gretima pusė/hipotenuzė

Vadinasi, cot θ = cos θ/sin θ

Kotangentinė funkcija sinusinės funkcijos atžvilgiu gali būti parašyta kaip,

lovelė θ = (√1 – nuod ² i)/nuodėmė i

Žinome, kad cot θ = cos θ/sin θ

Iš mūsų turimų pitagoriečių tapatybių;

cos²θ + nuodėmė²θ = 1

⇒ cos θ = √1 – nuodėmė²i

Vadinasi, vaikiška lovelė θ = $frac{sqrt{left(1-sin^{2} heta ight)}}{sin heta}$

Kotangentinė funkcija, kalbant apie kosinuso funkciją, gali būti parašyta kaip,

vaikiška lovelė θ = cos θ/(√1 -cos ² i)

Žinome, kad cot θ = cos θ/sin θ

Iš mūsų turimų pitagoriečių tapatybių;

cos²θ + nuodėmė²θ = 1

sin θ = √1 – cos²i

Vadinasi, vaikiška lovelė θ = $frac{cos heta}{sqrt{left(1-cos^{2} heta ight)}}$

Kotangentinė funkcija, kalbant apie sekantines ir kosekantines funkcijas, gali būti parašyta kaip,

cot θ = cosec θ/sec θ

Turime, cot θ = cos θ/sin θ

Tai gali būti parašyta kaip, cot θ = (1/sin θ) / (1/cos θ)

⇒ lovelė θ = cosec θ/sec θ

Kotangentinė funkcija, kalbant apie kosekantinę funkciją, gali būti parašyta taip:

vaikiška lovelė θ = √ (kosek ² -1)

Iš pitagoriečių tapatybių mes turime,

cosec²θ – vaikiška lovelė²θ = 1

⇒ vaikiška lovelė²θ = 1 – kosek²– 1

Vadinasi, vaikiška lovelė θ = √ (kosek²-1)

Kotangentinė funkcija, kalbant apie sekantinę funkciją, gali būti parašyta taip:

vaikiška lovelė θ = 1/(√s ² aš - 1)

Iš pitagoriečių tapatybių mes turime,

sek²θ – taip²θ = 1

tan θ = √sek²aš - 1

Mes žinome, kad vaikiška lovelė θ = 1/tan θ
įdiegti maven

Vadinasi, vaikiška lovelė θ = $frac{1}{sqrt{left(1-sec^{2} heta ight)}}$

Trigonometrinių santykių lentelė

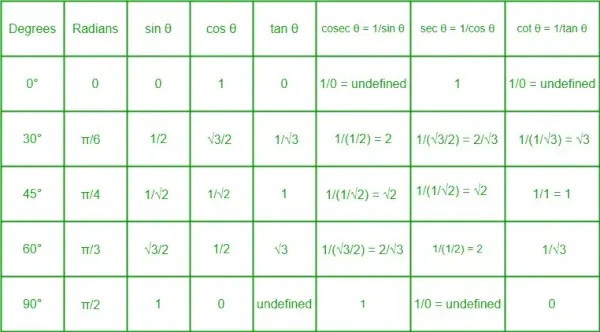
Trigonometrinių santykių lentelė

Kotangentų dėsnis arba kotangentų įstatymas

Kotangento dėsnis atrodo panašus į sinuso dėsnį, tačiau čia jis apima pusę kampų. Kotangentų dėsnis apibūdina ryšį tarp trikampio kraštinių ilgių ir trijų kampų pusių kotangentų. Apsvarstykite trikampį ABC, kur a, b ir c yra trikampio kraštinių ilgiai.

Kotangentų dėsnis teigia, kad

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

Kur s yra trikampio ABC pusperimetras, o r yra jo įbrėžto trikampio apskritimo spindulys.

s = (a + b + c)/2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

Pavyzdinės problemos

1 uždavinys: Raskite lovos θ reikšmę, jei tan θ = 3/4.

Sprendimas:

Pateiktais duomenimis, tan θ = 3/4

Mes tai žinome, vaikiška lovelė θ = 1/tan θ

⇒ vaikiška lovelė θ = 1/(3/4) = 4/3

Taigi, vaikiška lovelė θ = 4/3

2 uždavinys: Raskite cot α, sin α = 1/3 ir cos α = 2√2/3 reikšmę.

Sprendimas:

Pateikti duomenys, sin α = 1/3 ir cos α = 2√2/3

Mes tai žinome, lovelė α = cos α/sin α

⇒ vaikiška lovelė α = (2√2/3) / (1/3) = 2√2

Vadinasi, lovelės reikšmė α = 2√2

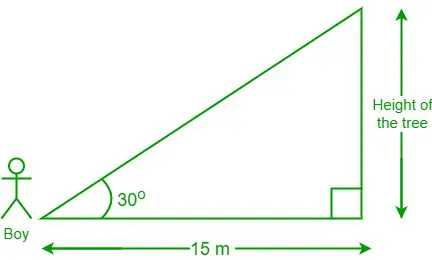
3 problema: 15 m nuo medžio stovintis berniukas žiūri 30 laipsnių kampu į medžio viršūnę. Koks yra medžio aukštis?

Sprendimas:

Diagrama iš pateiktų duomenų

Pateiktais duomenimis atstumas tarp berniuko ir medžio pėdos = 15 m ir θ = 30°

Tegul medžio aukštis yra „h“

Mes turime, lovelė θ = gretima pusė / priešinga pusė

⇒ vaikiška lovelė 30° = 15/val

⇒ √3 = 15/h [nes, vaikiška lovelė 30° = √3]

⇒ h = 15/√3

⇒ h = 5√3 m

Vadinasi, medžio aukštis = 5√3 m

4 uždavinys: Raskite lovos x reikšmę, jei sek x = 6/5.

Sprendimas:

Pateikti duomenys, sek x = 6/5

Mes turime, sek ² x – taip ² x = 1

⇒ (6/5)²-taip²x = 1

⇒ 36/25 – taip²x = 1

⇒ taip²x = 36/25 – 1

⇒ taip²x = 11/25

⇒ įdegis x = √(11/25) = √11/5

Mes tai žinome, vaikiška lovelė x = 1 / įdegis x

⇒ vaikiška lovelė x = 1/(√11/5) = 5/√11

Vadinasi, vaikiška lovelė x = 5/√11

5 uždavinys: Raskite lovos θ reikšmę, jei cosec θ = 25/24.

Sprendimas:

Pateikti duomenys, cosec θ = 25/24

Mes tai žinome, vaikiška lovelė θ = √ (kosek ² -1)

⇒ vaikiška lovelė θ = √ (25/24)²– 1

⇒ vaikiška lovelė θ = √(625–576)/576 = √49/576

⇒ vaikiška lovelė θ = 7/24

Vadinasi, lovelės θ vertė = 7/24

6 uždavinys: Raskite lovos β reikšmę, jei sin β = 5/13.

Sprendimas:

Pateiktais duomenimis, sin β = 5/13

Mes tai žinome, be ² β + cos ² β = 1

⇒ (5/13)²+ cos²β = 1

⇒ cos²β = 1 – (5/13)²= 1 – 25/169 = 144/169

⇒ cos β = √144/169 = 12/13

lovelė β = cosβ/sin β

= (12/13) / (5/13)

⇒ vaikiška lovelė β = 12/5

Vadinasi, lovelės β vertė = 12/5

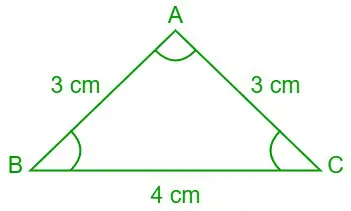
7 uždavinys: naudodamiesi kotangentų dėsniu raskite ∠A, ∠B ir ∠C reikšmes (laipsniais), jei trikampio ABC trijų kraštinių ilgiai yra a = 4 cm, b = 3 cm ir c= 3 cm.

Sprendimas:

Pateikta, a = 4 cm, b = 3 cm ir c = 3 cm

Trikampis ABC

Iš kotangentų įstatymo,

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

s = (a + b + c)/2

⇒ s = (3 + 4 + 3)/2 = 10/2 = 5

Dabar s – a = 5 – 4 = 1

⇒ s – b = 5 – 3 = 2

⇒ s – c = 5 – 3 = 2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

⇒ r = √[(1)(2)(2)/5]

Trikampio spindulys r = 2/√5
konvertuojant į eilutę

Iš kotangentų dėsnio lygties,

vaikiška lovelė (A/2)/1 = 1/(2/√5)

⇒ lovelė (A/2) = √5/2 ⇒ A/2 = vaikiška lovelė^-1(√5/2)

⇒ (A/2) = 41,8° ⇒ ∠A = 83,6°

lovelė (B/2)/2 = 1/(2/√5)

⇒ vaikiška lovelė (B/2) / 2 = √5/2 ⇒ lovelė (B/2) = √5

⇒ (B/2) = vaikiška lovelė^-1(√5) = 24,1° ⇒ ∠B = 48,2°

vaikiška lovelė (C/2)/2 = 1/(2/√5)

⇒ lovelė (C/2) = √5 ⇒ (C/2) = vaikiška lovelė^-1(√5)

⇒ (C/2) = 24,1° ⇒ ∠C = 48,2°

Vadinasi, trikampio ABC kampai yra ∠A = 83,6°, ∠B = 48,2° ir ∠C = 48,2°.