Logistinė regresija R programavime yra klasifikavimo algoritmas, naudojamas įvykio sėkmės ir nesėkmės tikimybei nustatyti. Logistinė regresija naudojama, kai priklausomasis kintamasis yra dvejetainio pobūdžio (0/1, teisingas/klaidingas, taip/ne). Logit funkcija naudojama kaip nuorodos funkcija dvinariame skirstinyje.
Dvejetainio rezultato kintamojo tikimybę galima numatyti naudojant statistinio modeliavimo metodą, vadinamą logistine regresija. Jis plačiai naudojamas daugelyje skirtingų pramonės šakų, įskaitant rinkodarą, finansus, socialinius mokslus ir medicinos tyrimus.
Logistinė funkcija, paprastai vadinama sigmoidine funkcija, yra pagrindinė logistinės regresijos idėja. Ši sigmoidinė funkcija naudojama logistinei regresijai apibūdinti koreliaciją tarp prognozuojamųjų kintamųjų ir dvejetainio rezultato tikimybės.

Logistinė regresija R programavime
Logistinė regresija taip pat žinoma kaip Binominė logistikos regresija . Jis pagrįstas sigmoidine funkcija, kai išvestis yra tikimybė, o įvestis gali būti nuo -begalybės iki +begalybės.
teorija
Logistinė regresija taip pat žinoma kaip apibendrintas tiesinis modelis. Kadangi jis naudojamas kaip klasifikavimo metodas kokybiniam atsakui numatyti, y reikšmė svyruoja nuo 0 iki 1 ir gali būti pavaizduota tokia lygtimi:

Logistinė regresija R programavime
p yra dominančios charakteristikos tikimybė. Šansų santykis apibrėžiamas kaip sėkmės tikimybė, palyginti su nesėkmės tikimybe. Tai yra pagrindinis logistinės regresijos koeficientų atvaizdas ir gali turėti reikšmes nuo 0 iki begalybės. Šansų santykis 1 yra tada, kai sėkmės tikimybė yra lygi nesėkmės tikimybei. Šansų santykis 2 yra tada, kai sėkmės tikimybė yra dvigubai didesnė už nesėkmės tikimybę. Šansų santykis 0,5 yra tada, kai nesėkmės tikimybė yra dvigubai didesnė už sėkmės tikimybę.
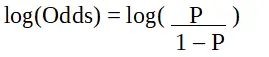
Logistinė regresija R programavime
Kadangi dirbame su dvejetainiu skirstiniu (priklausomu kintamuoju), turime pasirinkti šiam skirstiniui geriausiai tinkančią nuorodos funkciją.
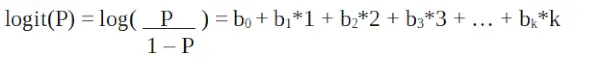
Logistinė regresija R programavime
Tai yra logit funkcija . Aukščiau pateiktoje lygtyje skliaustai pasirenkami siekiant padidinti imties verčių stebėjimo tikimybę, o ne sumažinti kvadratinių klaidų sumą (kaip įprasta regresija). Logit taip pat žinomas kaip šansų žurnalas. Logit funkcija turi būti tiesiškai susieta su nepriklausomais kintamaisiais. Tai yra iš lygties A, kur kairėje pusėje yra tiesinė x kombinacija. Tai panašu į OLS prielaidą, kad y yra tiesiškai susijęs su x. Kintamieji b0, b1, b2 ir tt yra nežinomi ir turi būti įvertinti pagal turimus treniruočių duomenis. Logistinės regresijos modelyje, padauginus b1 iš vieno vieneto, logit pasikeičia iš b0. P pokyčiai dėl vieno vieneto pasikeitimo priklausys nuo vertės, padaugintos. Jei b1 yra teigiamas, tada P padidės, o jei b1 yra neigiamas, tada P mažės.
Duomenų rinkinys
mtcars (variklio tendencijų automobilių kelių bandymas) apima degalų sąnaudas, našumą ir 10 automobilio dizaino aspektų 32 automobiliams. Jis yra iš anksto įdiegtas kartu su dplyr pakuotė R.
R
# Installing the package> install.packages>(>'dplyr'>)> # Loading package> library>(dplyr)> # Summary of dataset in package> summary>(mtcars)> |
>
>
Logistinės regresijos atlikimas duomenų rinkinyje
Logistinė regresija realizuojama R naudojant glm() lavinant modelį naudojant duomenų rinkinio ypatybes arba kintamuosius.
R
burbulas rūšiuoti java
# Installing the package> # For Logistic regression> install.packages>(>'caTools'>)> # For ROC curve to evaluate model> install.packages>(>'ROCR'>)> > # Loading package> library>(caTools)> library>(ROCR)> |
>
>
Duomenų padalijimas
R
# Splitting dataset> split <->sample.split>(mtcars, SplitRatio = 0.8)> split> train_reg <->subset>(mtcars, split ==>'TRUE'>)> test_reg <->subset>(mtcars, split ==>'FALSE'>)> # Training model> logistic_model <->glm>(vs ~ wt + disp,> >data = train_reg,> >family =>'binomial'>)> logistic_model> # Summary> summary>(logistic_model)> |
>
>
Išvestis:
Call: glm(formula = vs ~ wt + disp, family = 'binomial', data = train_reg) Deviance Residuals: Min 1Q Median 3Q Max -1.6552 -0.4051 0.4446 0.6180 1.9191 Coefficients: Estimate Std. Error z value Pr(>|z|) (Pertrauka) 1,58781 2,60087 0,610 0,5415 masė 1,36958 1,60524 0,853 0,3936 disp -0,02969 0,01577 -1,8598 0,0. --- Signif. kodai: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1 (Dvejonės šeimos dispersijos parametras laikomas 1) Nulinis nuokrypis: 34,617 esant 24 laisvės laipsniams Likutinis nuokrypis: 22 22 laisvės laipsniai AIC: 26.212 Fisher Scoring iteracijų skaičius: 6>
- Iškvietimas: rodomas funkcijos iškvietimas, naudojamas logistinei regresijos modeliui pritaikyti, kartu su informacija apie šeimą, formulę ir duomenis. Deviance Residuals: tai yra nuokrypių likučiai, kurie įvertina modelio tinkamumo laipsnį. Jie reiškia neatitikimus tarp faktinių atsakymų ir tikimybių, numatytų pagal logistinės regresijos modelį. Koeficientai: šie logistinės regresijos koeficientai parodo atsako kintamojo logo koeficientus arba logit. Standartinės paklaidos, susijusios su apskaičiuotais koeficientais, pateiktos Std. Klaidų stulpelis. Reikšmingumo kodai: kiekvieno nuspėjamojo kintamojo reikšmingumo lygis nurodomas reikšmingumo kodais. Dispersijos parametras: Logistinėje regresijoje dispersijos parametras naudojamas kaip dvinario skirstinio mastelio keitimo parametras. Šiuo atveju jis nustatytas į 1, o tai rodo, kad tariama dispersija yra 1. Nulinis nuokrypis: Nulinis nuokrypis apskaičiuoja modelio nuokrypį, kai atsižvelgiama tik į pertrauką. Tai simbolizuoja nuokrypį, atsirandantį dėl modelio be prognozių. Likutinis nuokrypis: liekamasis nuokrypis apskaičiuoja modelio nuokrypį pritaikius prognozes. Tai reiškia liekamąjį nuokrypį, atsižvelgus į prognozes. AIC: Akaike informacijos kriterijus (AIC), kuris atspindi prognozių skaičių, yra modelio tinkamumo matas. Tai bausti už sudėtingesnius modelius, kad būtų išvengta permontavimo. Geresnius modelius rodo mažesnės AIC reikšmės. Fišerio vertinimo iteracijų skaičius: Iteracijų skaičius, reikalingas Fišerio balų skaičiavimo procedūrai modelio parametrams įvertinti, nurodomas iteracijų skaičiumi.
Numatykite bandymo duomenis pagal modelį
R
t ff
predict_reg <->predict>(logistic_model,> >test_reg, type =>'response'>)> predict_reg> |
>
>
Išvestis:
Hornet Sportabout Merc 280C Merc 450SE Chrysler Imperial 0.01226166 0.78972164 0.26380531 0.01544309 AMC Javelin Camaro Z28 Ford Pantera L 0.06104267 0.02807992 0.01107943>
R
# Changing probabilities> predict_reg <->ifelse>(predict_reg>0,5, 1, 0)> # Evaluating model accuracy> # using confusion matrix> table>(test_reg$vs, predict_reg)> missing_classerr <->mean>(predict_reg != test_reg$vs)> print>(>paste>(>'Accuracy ='>, 1 - missing_classerr))> # ROC-AUC Curve> ROCPred <->prediction>(predict_reg, test_reg$vs)> ROCPer <->performance>(ROCPred, measure =>'tpr'>,> >x.measure =>'fpr'>)> auc <->performance>(ROCPred, measure =>'auc'>)> auc <- [email protected][[1]]> auc> # Plotting curve> plot>(ROCPer)> plot>(ROCPer, colorize =>TRUE>,> >print.cutoffs.at =>seq>(0.1, by = 0.1),> >main =>'ROC CURVE'>)> abline>(a = 0, b = 1)> auc <->round>(auc, 4)> legend>(.6, .4, auc, title =>'AUC'>, cex = 1)> |
>
>
Išvestis:
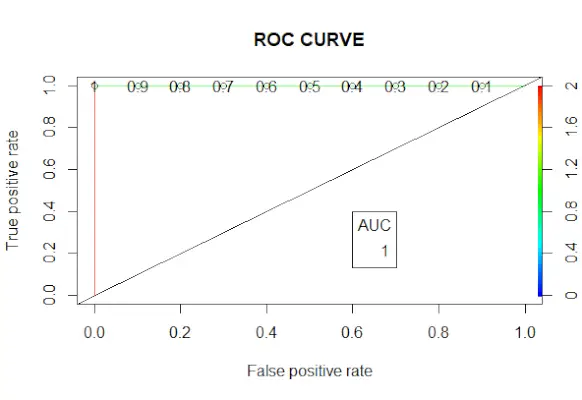
ROC kreivė
2 pavyzdys:
Galime atlikti logistinės regresijos modelio Titaniko duomenų rinkinį R.
R
# Load the dataset> data>(Titanic)> # Convert the table to a data frame> data <->as.data.frame>(Titanic)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # View the summary of the model> summary>(model)> |
>
skirtumas tarp tigro ir liūto
>
Išvestis:
Call: glm(formula = Survived ~ Class + Sex + Age, family = binomial, data = data) Deviance Residuals: Min 1Q Median 3Q Max -1.177 -1.177 0.000 1.177 1.177 Coefficients: Estimate Std. Error z value Pr(>|z|) (Pertrauka) 4.022e-16 8.660e-01 0 1 Class2nd -9.762e-16 1.000e+00 0 1 Class3rd -4.699e-16 1.000e+00 0 1 ClassCrew -5.651.0-1.651.0 00 0 1 Lytis Moteris -3.140e-16 7.071e-01 0 1 Amžius Suaugęs 5.103e-16 7.071e-01 0 1 (Dvejonės šeimos dispersijos parametras laikomas 1) Nulinė nuokrypis: 44,1361 laisvės nuokrypis 1.4:4. ant 26 laisvės laipsnių AIC: 56.361 Fisher Scoring iteracijų skaičius: 2>
Nubraižykite Titaniko duomenų rinkinio ROC kreivę
R
# Install and load the required packages> install.packages>(>'ROCR'>)> library>(ROCR)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # Make predictions on the dataset> predictions <->predict>(model, type =>'response'>)> # Create a prediction object for ROCR> prediction_objects <->prediction>(predictions, titanic_df$Survived)> # Create an ROC curve object> roc_object <->performance>(prediction_obj, measure =>'tpr'>, x.measure =>'fpr'>)> # Plot the ROC curve> plot>(roc_object, main =>'ROC Curve'>, col =>'blue'>, lwd = 2)> # Add labels and a legend to the plot> legend>(>'bottomright'>, legend => >paste>(>'AUC ='>,>round>(>performance>(prediction_objects, measure =>'auc'>)> >@y.values[[1]], 2)), col =>'blue'>, lwd = 2)> |
>
>
Išvestis:
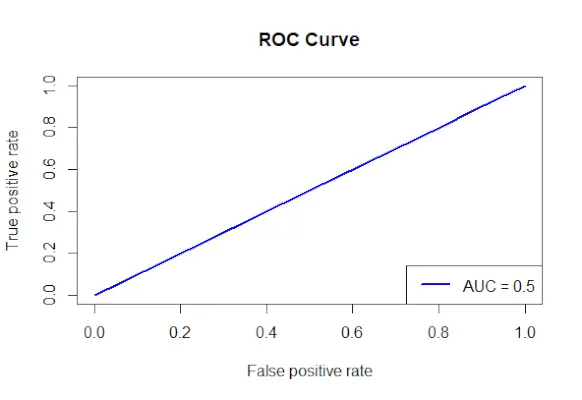
ROC kreivė
- Nurodomi veiksniai, naudojami prognozuoti išgyvenusius, o formulė Išgyvenusi klasė + lytis + amžius naudojama logistinės regresijos modeliui sukurti.
- Naudojant prognozę() funkciją, prognozės daromos duomenų rinkinyje naudojant pritaikytą modelį.
- Numatomos tikimybės derinamos su faktinėmis rezultato reikšmėmis, kad būtų sukurtas numatymo objektas naudojant prognozavimo() metodą iš ROCR paketo.
- Nurodomas tikrojo teigiamo rodiklio (tpr) matas ir klaidingai teigiamo greičio (fpr) x ašies matas, o ROC kreivės objektas sukuriamas naudojant funkciją performance () iš ROCR paketo.
- ROC kreivės objektas (roc_obj), nurodantis pagrindinį pavadinimą, spalvą ir linijos plotį, brėžiamas naudojant plot() funkciją.
- Jis naudoja funkciją performance() su meetu = auc, kad nustatytų AUC (sritis po kreive) reikšmę ir prideda prie diagramos etiketes ir legendą.
