Būtina sąlyga – duomenų gavyba , panašumo matas reiškia atstumą su matmenimis, atspindinčiais duomenų objekto ypatybes duomenų rinkinyje. Jei šis atstumas mažesnis, panašumo laipsnis bus didelis, o kai atstumas didelis, panašumo laipsnis bus mažas. Kai kurios populiarios panašumo priemonės yra:
- Euklido atstumas.
- Manheteno atstumas.
- Jaccard panašumas.
- Minkovskio atstumas.
- Kosinuso panašumas.
Kosinuso panašumas yra metrika, padedanti nustatyti, kiek duomenų objektai yra panašūs, nepaisant jų dydžio. Dviejų sakinių panašumą Python galime išmatuoti naudodami kosinuso panašumą. Pagal kosinuso panašumą duomenų rinkinio duomenų objektai yra traktuojami kaip vektorius. Formulė, leidžianti rasti dviejų vektorių kosinuso panašumą:
(x, y) = x . y / ||x|| ||y||>
kur,
- x . y = vektorių „x“ ir „y“ sandauga (taškas).||x|| ir ||ir|| = dviejų vektorių „x“ ir „y“ ilgis (dydis).||x||
||ir|| = reguliarioji dviejų vektorių „x“ ir „y“ sandauga. Pavyzdys : Apsvarstykite pavyzdį, kad surastumėte panašumą tarp dviejų vektorių - 'x' ir 'ir' , naudojant kosinuso panašumą. „x“ vektorius turi vertes, x = { 3, 2, 0, 5 } „Y“ vektorius turi reikšmes, y = {1, 0, 0, 0} Kosinuso panašumo apskaičiavimo formulė yra tokia: 
(x, y) = x. y / ||x|| ||ir||
x . y = 3*1 + 2*0 + 0*0 + 5*0 = 3 ||x|| = √ (3)^2 + (2)^2 + (0)^2 + (5)^2 = 6.16 ||y|| = √ (1)^2 + (0)^2 + (0)^2 + (0)^2 = 1 ∴ (x, y) = 3 / (6.16 * 1) = 0.49>
Skirtumas tarp dviejų vektorių „x“ ir „y“ nustatomas taip:
∴ (x, y) = 1 - (x, y) = 1 - 0.49 = 0.51>
- Dviejų vektorių kosinuso panašumas matuojamas „θ“.
- Jei θ = 0°, „x“ ir „y“ vektoriai sutampa, taip įrodant, kad jie yra panašūs.
- Jei θ = 90°, „x“ ir „y“ vektoriai yra nepanašūs.
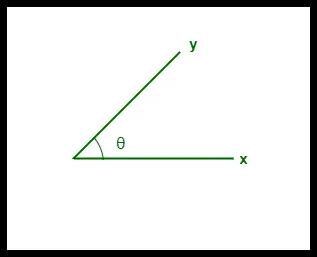
Kosinuso panašumas tarp dviejų vektorių
Privalumai:
- Kosinuso panašumas yra naudingas, nes net jei du panašūs duomenų objektai dėl dydžio nutolę vienas nuo kito Euklido atstumu, jie vis tiek gali turėti mažesnį kampą tarp jų. Kuo mažesnis kampas, tuo didesnis panašumas.
- Kai brėžiama daugiamatėje erdvėje, kosinuso panašumas užfiksuoja duomenų objektų orientaciją (kampą), o ne dydį.