Kampas tarp dviejų vektorių yra kampas tarp jų uodegų ir šį kampą galima lengvai rasti naudojant vektorinių formulių kryžminę sandaugą ir taškinę sandaugą. Kampas tarp dviejų vektorių visada yra nuo 0° iki 180°.
Šiame straipsnyje mes sužinosime apie kampą tarp dviejų vektorių, apibrėžimą, formules ir išsamius pavyzdžius.
Kas yra kampas tarp dviejų vektorių?
Kampas tarp dviejų vektorių yra kampas, susidaręs jų uodegų sankirtoje. Kampas tarp dviejų vektorių gali būti ūminis, dešinysis arba bukas, priklausomai nuo vektorių krypties.
Kampas tarp dviejų vektorių randamas naudojant dvi formules:
- Vektorių taškinio produkto naudojimas
- Kryžminio vektorių sandaugos naudojimas
Tai paaiškinta toliau pateiktoje formulėje.
Kampas tarp dviejų vektorių formulės
Kampas tarp dviejų vektorių yra lengvai ir dažniausiai randamas naudojant vektorių skaliarinę sandaugą.
css teksto lygiavimas

Du vektoriai A ir B
Taškinis produktas A ir B yra pateikta taip,
vec{A}.vec{B} = |A| |B| cosθ.
Ypatingi atvejai
- Kai kampas tarp vektorių yra 0 laipsnių.
Tai yra θ = 0°
⇒ |A| |B| cosθ
⇒ |A| |B| cos0°
⇒ |A| |B| [cos0° = 1]
- Kai kampas tarp vektorių yra 180 laipsnių.
⇒ |A| |B| cosθ
⇒ |A| |B| cos180°
⇒ – |A| |B| [cos180° = -1]
- Kai kampas tarp vektorių yra 90 laipsnių.
⇒ |A| |B| cosθ
⇒ |A| |B| cos90°
⇒ |A| |B| × 0 [cos90° = 0]
⇒ 0
Kampo tarp dviejų vektorių formulė
Kampo tarp dviejų vektorių kosinusas yra lygus atskirų dviejų vektorių sudedamųjų dalių sandaugos sumai, padalytai iš dviejų vektorių dydžio sandaugos.
Du vektoriai A ir B
cosθ=
θ= cos-1
Dekarto forma,
A = Axi + Airj + ASuk
B = Bxi + Birj + BSuk
cos θ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}
„Dot“ gaminio savybės
- Taškinis produktas yra keičiamas
vec{A}.vec{B}=vec{B}.vec{A}
- Taškinis produktas yra platinamas
vec{A}.(vec{B}+vec{C})=(vec{A}.vec{B}+vec{A}.vec{C})
Kampas tarp dviejų vektorių yra tarp 0 ≤ θ ≤ 180. Kai abiejų vektorių uodegos arba galvutės sutampa, tada apskaičiuojamas kampas tarp vektorių.
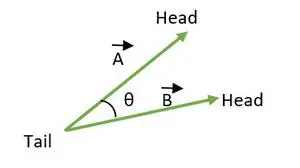
Uodega sutampa
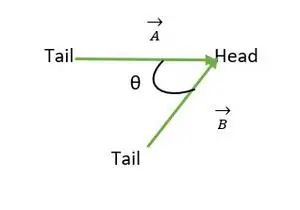
Galva sutampa
Pavyzdiniai uždaviniai Kampo tarp dviejų vektorių formulė
1 uždavinys: suraskite kampą tarp vektorių (jei jie sudaro lygiakraštį trikampį)
- a ir b vektoriai
- b ir c vektoriai
- a ir c vektoriai
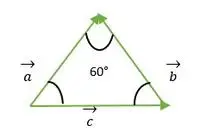
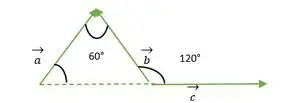
Lygiakraštis trikampis, sudarytas iš a, b, c vektoriaus
Sprendimas:
- a ir b vektoriai
Vektorių a ir b atveju abiejų vektorių galva sutampa vienas su kitu, taigi kampas tarp a ir b vektoriaus yra toks pat kaip kampas tarp dviejų lygiakraščio trikampio kraštinių = 60°.
- b ir c vektoriai:
Iš aukščiau pateikto paveikslo matome, kad b ir c vektoriaus galva arba uodega nesutampa vienas su kitu.
Taigi, naudojant savybę- vektorius išlieka nepakitęs, jei jis perduodamas lygiagrečiai sau.
Vektorius c yra perkeltas lygiagrečiai sau
Dabar matome, kad vektorių b ir c uodega sutampa vienas su kitu, todėl yra toks pat kaip išorinis kampas su lygiakraščiu trikampiu = 120°.
- a ir c vektoriai
A ir c uodega sutampa
Vektorių a ir c atveju abiejų vektorių galai sutampa vienas su kitu, taigi kampas tarp a ir c vektoriaus yra toks pat kaip kampas tarp dviejų lygiakraščio trikampio kraštinių = 60°.
2 uždavinys: Raskite kampus tarp vektorių, jei jie sudaro lygiašonį stačiakampį trikampį.
- a ir b vektorius
- b ir c vektorius
- a ir c vektoriai
Sprendimas:
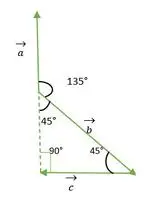
- a ir b vektorius
Stačiakampis Lygiašonis trikampis
Iš aukščiau pateikto paveikslo matome, kad a ir b vektoriaus galva arba uodega nesutampa vienas su kitu. Taigi, naudojant savybę- A vektorius išlieka nepakitęs, jei jis perduodamas lygiagrečiai sau.
vektorius perkeliamas lygiagrečiai sau
Dabar a ir b vektorių uodegos sutampa viena su kita ir sudaro tokį pat kampą kaip išorinis stačiakampio lygiašonio trikampio kampas = 135°.
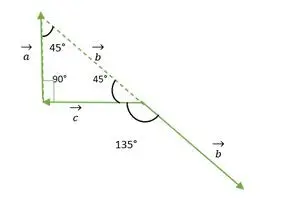
- b ir c vektorius
Stačiakampis Lygiašonis trikampis
Iš aukščiau pateikto paveikslo b ir c vektoriaus galvutė arba uodegos nesutampa. Taigi, naudojant savybę, vektorius išlieka nepakitęs, jei jis perduodamas lygiagrečiai sau.
b vektorius perkeliamas lygiagrečiai sau
Dabar b ir c vektorių uodegos sutampa viena su kita ir sudaro tokį pat kampą kaip išorinis stačiakampio lygiašonio trikampio kampas = 135°.
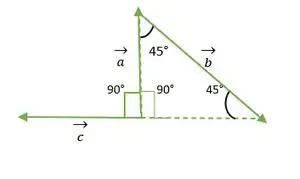
- a ir c vektoriai
Stačiakampis Lygiašonis trikampis
Iš aukščiau pateikto paveikslo a ir c vektoriaus galvutė arba uodegos nesutampa. Taigi, naudojant savybę- A vektorius išlieka nepakitęs, jei jis perduodamas lygiagrečiai sau.
c vektorius perkeliamas lygiagrečiai sau
Dabar a ir c vektorių uodegos sutampa viena su kita ir sudaro tokį pat kampą kaip lygiašonio trikampio stačiakampis = 90°.
3 uždavinys: Raskite kampą tarp vektorių A = i + j + k ir vektoriaus B = -2i – 2j – 2k.
Sprendimas:
Iš formulės,
A = Axi + Airj + ASuk
B = Bxi + Birj + BSuk
cosθ=
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Čia, duotame klausime,
A= i + j + k
B= -2i -2j -2k
Reikšmių pakeitimas formulėje
⇒ cosθ =
frac{(1.(-2)+1.(-2)+1.(-2))}{(sqrt{1^2+1^2+1^2}×sqrt{(-2)^2+(-2)^2+(-2)^2})} ⇒ cosθ =
frac{(-2-2-2)}{(sqrt{1+1+1}×sqrt{4+4+4})} ⇒ cosθ =
frac{-6}{(sqrt{3}×sqrt{12})} ⇒ cosθ =
frac{-6}{(sqrt{36})} ⇒ cosθ = -6/6
⇒ cosθ= -1
⇒ θ = 180°
4 uždavinys: Raskite kampą tarp vektoriaus A = 3i + 4j ir B = 2i + j
Sprendimas:
A = Axi + Airj + ASuk
B = Bxi + Birj + BSuk
cosθ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Čia duota,
A= 3i + 4j + 0k
B= 2i + j + 0k
Formulės reikšmių pakeitimas,
⇒ cosθ =
frac{(3.2+4.1+0.0)}{(sqrt{3^2+4^2+0^2}×sqrt{2^2+1^2+0^2})} ⇒ cosθ =
frac{(6+4+0)}{(sqrt{9+16+0}×sqrt{4+1+0})} ⇒ cosθ =
frac{(10)}{(sqrt{25}×sqrt{5})} ⇒ cosθ =
frac{(10)}{(sqrt{125})} ⇒ θ = cos-1(
frac{(10)}{5.(sqrt{5})} )pakeiskite eilutę Java⇒ θ = cos-1(
frac{2}{(sqrt{5})} )
5 uždavinys: Raskite kampą tarp vektoriaus A = i + j ir vektoriaus B = j + k.
Sprendimas:
Iš formulės,
A = Axi + Airj + ASuk
B = Bxi + Birj + BSuk
cosθ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Čia, duotame klausime,
⇒ A = i + j
⇒ B = j + k
⇒ cosθ =
frac{(1.0+1.1+0.1)}{(sqrt{1^2+1^2+0^2}×sqrt{0^2+1^2+1^2})} ⇒ cosθ =
frac{(1)}{(sqrt{1+1+0}×sqrt{0+1+1})} ⇒ cosθ =
frac{1}{(sqrt{2}×sqrt{2})} ⇒ θ = cos-1(1/2)
⇒ θ = 60°