
Daugelį studentų, besimokančių SAT, labiausiai gąsdina matematikos skyrius. Yra daug klausimų, susijusių su daugybe temų, į kuriuos reikia atsakyti per trumpą laiką. Laimei, galite įeiti į egzaminų kambarį jausdami pasiruošę ir pasitikėdami SAT matematika. Šiame vadove yra 16 geriausių SAT matematikos patarimų ir gudrybių, kuriuos turėtumėte naudoti. Jie apima visus pagrindus nuo to laiko, kai pradedate mokytis, iki to momento, kai iššaukiamas laikas egzaminui ir jūs padedate pieštuką.
SAT Math apžvalga
Prieš pasinerdami į SAT matematikos gudrybes, trumpai apžvelgsime šios egzamino dalies formatą. SAT matematika yra padalinta į dvi dalis. Pirmiausia užpildysite 25 minučių skyrių, kurio metu negalėsite naudotis skaičiuokle. Po trumpos pertraukėlės pereisite į 55 minučių atkarpą. Šioje ilgesnėje dalyje jums leidžiama naudoti skaičiuotuvą.
Abu skyriai prasidės klausimų su daugybe atsakymų variantų, kurių kiekviename bus keturi atsakymų variantai. Tada jūsų bus paprašyta pateikti kai kuriuos mokinių pateiktus atsakymus, labiau žinomus kaip „tinkleliai“. Neturėsite atsakymų į šiuos klausimus ir turėsite patys užpildyti teisingą atsakymą. Skaičiuoklės skiltyje kai kurie iš šių tinklelių bus susiję vienas su kitu kaip išplėstinio mąstymo klausimo dalis.
Čia pateikiamas laiko, klausimų skaičius ir klausimų tipai dviejuose SAT matematikos skyriuose.
| Skyrius | Klausimų skaičius | Laikas |
| Nėra skaičiuoklės | 15 kelių pasirinkimų, 5 tinkleliai | 25 minutes |
| Skaičiuoklė | 30 kelių pasirinkimų, 8 tinkleliai (įskaitant vieną išplėstinio mąstymo klausimą) | 55 minutes |
| Iš viso | 58 klausimai | 80 minučių |
SAT matematikos gudrybės, kurias reikia naudoti prieš bandymo dieną
Naudokitės šiais SAT matematikos patarimais, kol mokysitės testui, kad gerai pasiruoštumėte, kol sėsite laikyti SAT.
1: žinokite, kokia matematika bus tikrinama
Sunku gerai išlaikyti testą, jei nežinai, kokiais dalykais jis tave išbandys. Priklausomai nuo jūsų mokyklos ir matematikos pamokų tipus, kuriuos lankėte , galite pastebėti, kad SAT Math testų temos visiškai skiriasi nuo tos, kurias nagrinėjote matematikos pamokoje. Temos gali būti įgūdžiai, kuriuos išmokote prieš daugelį metų arba niekada net neaptarėte. Bet kuris scenarijus tinkamas; svarbu, kad žinotumėte, dėl ko būsite tikrinami, kad galėtumėte studijuoti tinkamas temas. Čia yra visi 24 įgūdžiai, išbandyti SAT matematikoje:- Linijinės funkcijos
- Vieno kintamojo lygtys
- Tiesinių lygčių sistemos
- Absoliučioji vertė
- Manipuliavimas daugianariais
- Kvadratinės lygtys
- Daugiavardžių dalybos
- Eksponentinės funkcijos
- Funkcijos žymėjimas
- Eksponentinių lygčių sprendimas
- Lygčių sistemos su netiesinėmis lygtimis
- Santykiai ir proporcijos
- Taškinės diagramos ir grafikai
- Kategoriniai duomenys ir tikimybės
- Eksperimentinė interpretacija
- Medana, mediana, režimas, standartinis nuokrypis
- Koordinačių geometrija – linijos ir šlaitai
- Koordinačių geometrija – netiesinės funkcijos
- Geometrija – apskritimai
- Geometrija – linijos ir kampai
- Geometrija – kietoji geometrija
- Geometrija – trikampiai ir daugiakampiai
- Trigonometrija
- Sudėtingi skaičiai
-
- Viename stulpelyje užpildykite ne daugiau kaip vieną apskritimą
- Jei atsakymas neužima visų keturių tarpų (pvz., 8, 17 arba 347), galite jį pradėti bet kuriame stulpelyje. Pavyzdžiui, jei atsakymas yra 201, bet kuris toliau pateiktas atsakymas yra teisingas:
-
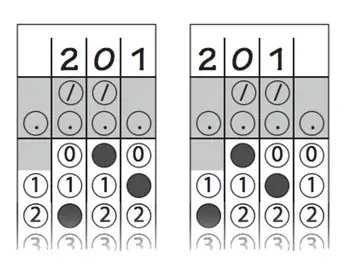
- Atminkite, kad jūsų atsakymas niekada negali būti neigiamas skaičius (nes jokiu būdu negalima burbuliuoti neigiamo ženklo).
- Niekada neįtrauksite pi į savo atsakymą; naudosite dešimtainį skaičių. Pavyzdžiui, 3π būtų parašytas kaip 9,425.
- Galite rašyti atsakymus trupmenomis arba po kablelio, bet negalite naudoti mišrių skaičių. Pvz., 3 ½ tinklelyje turėtumėte nurodyti 7/2 arba 3,5, nes rūšiavimo mašina 3 ½ rodytų kaip 31/2.
- Kai kurie klausimai turės daugiau nei vieną atsakymą (paprastai jie jums tai pasakys klausime). Tik tinklelis viename atsakyme. Pavyzdžiui, jei jūsų paprašys vienos x reikšmės, todėl ( x −1)( x −3)=0, tada atsakymai yra x = 3 arba x =1, ir jūs turėtumėte pasirinkti tinklelį 1 arba 3.
Jei yra kokių nors temų, kurių jau esate tikras, kad nežinote, galite pažymėti jas, kad galėtumėte jas studijuoti. Šis sąrašas taip pat bus naudingas atlikus tam tikrus praktikos testus (žr. 3 patarimą), kad galėtumėte nustatyti sritis, kuriose jums sekasi, ir sritis, kurias reikia tobulinti.

#2: įsiminkite įprastas formules ir matematikos faktus
SAT matematikoje, 12 svarbių formulių, kurios turi būti įtrauktos į abiejų matematikos skyrių pradžioje. Galite remtis šiomis formulėmis visoje SAT Math, bet jei kiekvieną kartą, kai jums reikia ieškoti formulės, pereisite į skyriaus priekį, sugaišite brangų laiką. Geriausia visas formules išmokti atmintinai prieš egzamino dieną. Peržiūrėkite mūsų straipsnį apie formules, kurias reikia žinoti SAT matematikos skyriui, kad pamatytumėte, kurias formules turėsite testo dieną, taip pat kitas matematikos formules ir faktus, kuriuos turėjote įsiminti.
#3: atlikite aukštos kokybės praktinius testus
SAT matematiką galite tobulėti tik tada, kai naudojate aukštos kokybės praktikos testus ir, deja, ten yra daug nekokybiškos studijų medžiagos. Naudodami žemos kokybės praktinę medžiagą galite sumažinti jūsų balą, nes galite studijuoti neteisingą informaciją ir praleisti tai, ko jums reikia.
Absoliučiai geriausias SAT matematikos klausimų šaltinis yra oficialūs SAT testai . Juos gamina tie patys žmonės, kurie kuria tikrąjį SAT, todėl žinote, kad jie tiksliai supras, kokios yra SAT problemos. Rekomenduojame bent dvi SAT matematikos dalis atlikti pagal laiką ir vienu prisėdimu, kad galėtumėte priprasti prie matematikos skyriaus ilgio ir laiko spaudimo. Taip pat turėtumėte pasistengti atlikti kelis pilno ilgio SAT, nustatytu laiku ir vienu prisėdimu, kad pamatytumėte, kokią įtaką jums paveiks kelias valandas trunkantis bandymas.
Daugelis studentų taip pat mėgsta mokytis naudodami parengiamąsias knygas. Jei esate vienas iš jų, peržiūrėkite mūsų straipsnį apiegeriausios SAT matematikos knygos. Visi jie turi aukštos kokybės praktikos testus ir klausimus, kurie taip pat gali padėti jums mokytis.
4: mokykitės iš savo klaidų
Nepakanka įveikti dešimtis ar net šimtus praktikos problemų. Po to turite išanalizuoti kiekvieną klausimą, į kurį atsakėte. Kiekviena klaida, kurią padarėte atliekant testą, įvyksta dėl priežasties. Jei tiksliai nesuprantate, kodėl praleidote šį klausimą, tą klaidą darysite vėl ir vėl.
Kiekviename praktikos teste ar klausimų rinkinyje pažymėkite kiekvieną klausimą, dėl kurio nesate tikri. Kai pataisysite savo atsakymus, peržiūrėkite kiekvieną klausimą, kurį suklydote, ir kiekvieną klausimą, kurį pažymėjote, kad nesate tikri. Tokiu būdu, net jei teisingai atspėjote klausimą, būtinai jį peržiūrėsite.
Kiekvienam klausimui išsiaiškinkite, kaip išspręsti problemą (žr. 5 patarimą) ir supraskite, kodėl nežinojote, kaip ją išspręsti. Jei pastebite, kad daug problemų yra tam tikroje srityje (pvz., geometrijoje), tuomet žinote, kad daugiau laiko reikia skirti konkrečiai šiai temai apžvelgti. Negalima paneigti, kad šie veiksmai užtruks, tačiau jie yra absoliučiai geriausias būdas išnaudoti visas praktikos testų galimybes ir iš tikrųjų pamatyti savo SAT matematikos balo patobulinimus.
Nr. 5: Pakartokite klausimus, kuriuos suklydote prieš žiūrėdami į atsakymo paaiškinimą
Kai pateikiate neteisingą klausimą, pirmiausia tikriausiai pažiūrėkite, koks yra teisingas atsakymas, ir tada perskaitykite atsakymo paaiškinimą. Tačiau tai nėra geriausias būdas mokytis SAT matematikos! Tai pasyvus mokymasis; jūs aktyviai nedalyvaujate klaidoje, kurią padarėte.
Mes rekomenduojame kitokį požiūrį. Raskite teisingą atsakymo pasirinkimą (A–D), kaip įprastai, bet nežiūrėkite į paaiškinimą. Vietoj to, pabandykite iš naujo išspręsti klausimą, kad sužinotumėte, ar žinodami, koks yra teisingas atsakymas, galite išsiaiškinti, kaip teisingai išspręsti klausimą.
Tiesą sakant, tai gali būti sunku. Jei pirmą kartą negavote tinkamo klausimo, paprastai nėra lengva jį teisingai atsakyti bandant dar kartą. Tačiau dabar, kai žinote teisingą atsakymą ir jums netrūksta laiko, galite pastebėti naują strategiją arba galvoti apie naują problemos sprendimo būdą.
Kai tai atsitiks ir jūs teisingai išsprendžiate problemą, tai, ką išmokote, daug ilgiau išliks jūsų mintyse nei jei ką tik būtum perskaitęs atsakymo paaiškinimą. Kadangi aktyviai dirbote, kad išspręstumėte problemą ir pasiektumėte proveržį, šią informaciją išsaugote daug geriau, nei tiesiog pasyviai įsisavindami informaciją. Tai vienas geriausių būdų mokytis iš klaidų ir iš tikrųjų sustiprinti savo silpnąsias vietas.
6: sutelkite savo studijas į sritis, kuriose kovojate daugiausiai
Štai keletas gerų naujienų: galbūt per daug laiko praleidžiate studijuodami! Vis dėlto kai kurioms SAT Math dalims. Kai kuriems studentams kyla pagunda iš karto perskaityti parengiamąsias knygas arba peržiūrėti medžiagą, tačiau jei yra dalykų, kuriuos jau gerai mokate, jums nereikia jų nuolat peržiūrėti. Veiksmingiausias būdas mokytis yra ne tik peržiūrėti visą galimą medžiagą; tai nukreipkite savo studijas, kad daugiausiai laiko praleistumėte tose srityse, kuriose jums reikia daugiausiai tobulėjimo. Čia reikia žinoti, kokių dalykų SAT matematikos testai ir praktikos testai atliekami. Jei žinote, kad esate tvirtas, tarkime, algebroje, bet nuolat pateikiate neteisingus geometrijos klausimus, turėtumėte skirti daug daugiau laiko geometrijos sąvokų studijoms ir geometrijos praktikos uždavinių atsakymui, nei skiriate algebros studijoms.

bash skaitymo failas
SAT matematikos patarimai, kuriuos reikia naudoti sprendžiant visus klausimus
Bandymo dieną ir atsakydami į praktikos klausimus naudokite šiuos SAT matematikos patarimus, kurie padės jums išspręsti visus klausimus, tiek su daugybe atsakymų, tiek į tinklelį.
#7: pabraukite pagrindines klausimo dalis
Tai vienas geriausių SAT matematikos gudrybių, kurias galite naudoti, jei darote neatsargias klaidas ir neteisingai pateikiate klausimus, nors žinote, kaip jas išspręsti. Kiekviename klausime pabraukite tai, ką turite rasti klausime, kad nesupainiotumėte skaičiavimo proceso metu.
Kartais SAT matematikos klausimai jūsų paprašys išspręsti vertę, dėl kurios reikia išspręsti ką nors kita (tarkime, kad jums reikia išspręsti x, kad galėtumėte rasti 4x reikšmę). Kad kažkas kitas (šiuo atveju x reikšmė) dažnai bus vienas iš neteisingų atsakymo pasirinkimų. Daugelis studentų netyčia pasirenka gudrų atsakymą, nes praranda vertę, kurią iš pradžių turėjo rasti. To galite išvengti pabraukdami atitinkamas klausimo dalis, kad išlaikytumėte savo dėmesį.
Štai pavyzdys:

Atsakydamas į šį klausimą, pabrėžčiau 300 USD plius 20 procentų jo pardavimų, 200 USD plius 25 procentai jos pardavimų, tiek pat pardavimų ir ta pati kompensacija bei kompensacija pabaigoje, kad primintų, ko aš ieškojau. Tai yra pagrindinė informacija, kurią turite žinoti, o matydami ją mažais gabalėliais galite lengviau suprasti ir prisiminti, palyginti su žiūrėjimu į teksto bloką. (Beje, teisingas atsakymas yra 700.)
# 8: žinokite savo laiką
Laiko spaudimas yra tai, ką turi žinoti beveik visi, naudojantys SAT, ir tai gali būti ypač didelė problema SAT matematikoje, kai nesunku pamiršti prabėgusių minučių skaičių, kai dirbate sprendžiant sudėtingą lygtį. . Tačiau labai svarbu sekti laiką egzamino metu, nes neatsakius į visus SAT matematikos klausimus gali būti sunku gauti norimą balą.
Pirmiausia žinokite, kiek turite laiko. Skiltyje Be skaičiuoklės turėsite 25 minutes atsakyti į 20 klausimų. Tai suteikia apie 75 sekundes vienam klausimui. Skaičiuoklės skiltyje turėsite 55 minutes atsakyti į 38 klausimus. Taip pat atminkite, kad kiekvienoje skiltyje pateikiami galutiniai klausimai ir į juos atsakymas dažnai užtrunka ilgiau.
Geriausias būdas greičiau mokytis SAT matematikos yra daug praktikuotis. Kai atsakysite į daugiau praktinių klausimų, susipažinsite su SAT Math klausimų stiliumi ir gudrybėmis, kurias bando naudoti testų autoriai.
Be to, neleiskite sau įstrigti ties klausimu ir gaišti daug laiko bandydami jį išspręsti. Kiekvienas matematikos klausimas vertas tiek pat taškų, todėl skirti dešimt minučių vienam klausimui teisingai atsakyti nėra gera strategija, jei dėl to kyla keli klausimai, į kuriuos net nežiūrėjote, kai ateina laikas. Jei su problema dirbate ilgiau nei minutę ir vis dar neįsivaizduojate, kaip ją išspręsti, pažymėkite ją savo bandomojoje knygelėje kaip tą, prie kurios reikia grįžti ir tęsti. Galite grįžti prie jo, jei turite laiko skyriaus pabaigoje.
# 9: įsitikinkite, kad išspręsite tinkamą vertę
SAT rašytojai mėgsta naudoti šį triuką: paprašykite mokinių išspręsti matematikos uždavinį (paprastai ilgą, kad klausimo instrukcijos nebūtų tokios šviežios jų mintyse), tada, išsprendę kintamąjį, jie užtikrintai pažymi savo atsakyk, bet suprask neteisingai! Kas nutiko? T ei, neišsprendė užduoto kintamojo.
Pažvelkite į šį pavyzdį:

Kaip sužinojote 7 patarime, perskaitę šį klausimą turėtumėte aiškiai pabraukti 2 kartus. Pateikiame problemą: „10+x yra 5 daugiau nei 10“. Klausime esantis žodis „yra“ nustato vienodus terminus, todėl išvertę šį teiginį gauname:
10+x=15
Dabar išskirkime savo kintamąjį.
10−10+x=15−10
x=5
Dabar dar kartą patikrinkime, prijungdami x atgal į pradinę lygtį.
10+x yra 5 daugiau nei 10.
10+5=15 yra 5 daugiau nei 10.
Puiku, mes išskyrėme savo kintamąjį. Bet čia SAT bando jus apgauti! Ar matote, kad 5 yra vienas iš atsakymo variantų? Jie tikisi, kad tai pamatysite, pamiršite, kad sprendžiate 2 kartus, ir pažymėsite tai kaip teisingą atsakymą.
Atminkite, kad klausimas nori, kad rastume 2x reikšmę, o ne tik x. x=5
2(5) = 10
Taigi mūsų galutinis atsakymas yra C, 2x=10.
#10: parodykite savo darbą
Jei lankėtės kurioje nors matematikos pamokoje, tikriausiai esate susipažinęs su daug kartų kartojama matematikos mokytojo mantra: parodykite savo darbą. Mokytojai nenori, kad atsakymą trauktum iš oro; jie nori, kad žingsnis po žingsnio parašytumėte, kaip išsprendėte problemą. Tai ne tik parodo jūsų supratimą, bet ir padeda pastebėti visas klaidas.
Dabar jūs negausite dalinių SAT matematikos įskaitų taip, kaip galite mokykloje, tačiau rodydami savo darbą SAT galite išlaikyti teisingą mąstymo procesą ir sumažinti neatsargių klaidų tikimybę.
Užrašykite visus atliktus skaičiavimus, taip pat kitų problemų sprendimo veiksmus, ar sprendžiate dėl x arba supaprastinant kelių kintamųjų išraišką. Daugeliui „No Calculator“ problemų reikia atlikti kelis veiksmus, todėl rašydami savo darbą galėsite sekti savo mąstymą ir išvengti klaidų.

11: žinokite, kada padėti skaičiuotuvą
Daugeliui SAT matematikos klausimų jums leidžiama naudoti skaičiuotuvą, tačiau tai ne visada reiškia, kad turėtumėte jį naudoti. Galima naudoti skaičiuotuvą greitam daugybai/sudėtinei arba, tarkime, kvadratinei šaknies paieškai, bet jei pradėsite bandyti spręsti klausimą naudodami sudėtingą kompiuterinę programą, žinokite, kad tikriausiai apsunkinate problemą, nei reikia. būti. Jokioms matematikos problemoms išspręsti nereikia skaičiuoklės programų. Tiesą sakant, kiekvienas SAT matematikos klausimas gali būti išspręstas be skaičiuoklės, nes egzamino rengėjai nenorėjo suteikti studentams, neturintiems skaičiuoklės, nesąžiningos kliūtys. Skaičiuoklė tiesiog leidžia greičiau ir lengviau išspręsti kai kuriuos klausimus.
Be to, atminkite, kad jei jūsų atsakymas nėra sveikas skaičius, skaičiuotuvas pateiks atsakymą dešimtainiu tikslumu, o kai kuriuos klausimus reikia atsakyti trupmenos forma. Tai reiškia, kad sugaišite laiką konvertuodami iš dešimtainių į trupmenas ir visada norėsite išmintingai naudoti savo laiką SAT.
SAT matematikos gudrybės atsakant į klausimus su keliais pasirinkimais
Pasinaudokite šiais SAT matematikos patarimais ir gudrybėmis atsakydami į egzamino klausimus su atsakymų variantais.
#12: pašalinkite 3 neteisingus atsakymus
Svarbiausia taisyklė, kurią reikia atsiminti atliekant SAT matematiką (kaip ir visus kitus SAT klausimus su atsakymų variantais), yra ta kiekvienam klausimui yra tik vienas teisingas atsakymas; kiti trys atsakymų variantai yra neabejotinai neteisingi. SAT turi mokėti apginti savo klausimus ir parodyti, kad į kiekvieną klausimą yra vienas ir tik vienas aiškus atsakymas. Testas labai susilpnėtų, jei žmonės galėtų nuolat ginčyti klausimus ir įtikinamai ginčytis, kad teisingas gali būti daugiau nei vienas atsakymas. Kolegijos taryba turėtų išmesti visus ginčijamus klausimus, todėl jiems liktų mažiau duomenų balams apskaičiuoti ir nepatikimumo reputacija.
Tai reiškia, kad jūsų strategija numeris vienas yra naudoti pašalinimo procesą. Jei jums sunku rasti teisingą klausimo sprendimą, pabandykite atmesti daugumą atsakymų, o ne priežastis, kodėl tam tikros parinktys galėtų būti naudingos. Visi neteisingi pasirinkimai yra neteisingi dėl rimtų priežasčių, ir jūsų darbas yra surasti tas priežastis, kol susiaurinsite savo atsakymus iki vienos galimybės.
#13: Įskiepių atsakymai problemoms spręsti
Kartais galite susidurti su problema, į kurią neįsivaizduojate, kaip spręsti, arba kurią, jūsų manymu, prireiks per ilgai išspręsti algebriškai. Kitais atvejais galbūt norėsite būti tikri, kad turite teisingą atsakymą į klausimą ir nepadarėte neatsargios klaidos. Kai taip nutinka, atsakymų prijungimas yra vienas geriausių SAT matematikos gudrybių, kurias reikia naudoti norint įsitikinti, kad gausite teisingą atsakymą.
Dar prieš pradėdami spręsti problemą, peržiūrėkite savo atsakymų pasirinkimą. Jei pirmiausia pažvelgsite į atsakymus (užuot bandę išspręsti problemą nuo nulio), jau žinosite diapazoną, į kurį turėtų patekti teisingas atsakymas. Pavyzdžiui, jei jūsų atsakymų diapazonas yra nuo 2 iki 20, žinote, kad teisingas atsakymas negali būti 35.
Dabar kokį atsakymo variantą turėtumėte prijungti pirmiausia? Atkreipkite dėmesį, kad SAT visada pateikia atsakymų pasirinkimus nuo mažiausio iki didžiausio (arba retais atvejais nuo didžiausio iki mažiausio). Mes visada rekomenduojame pradėti nuo atsakymo pasirinkimo C. Tai gali padėti jums susiaurinti laiką, skirtą įskiepiui atsakyti į klausimą, pradedant nuo vidurio ir naudojant pašalinimo procesą. Pavyzdžiui, jei pradedate nuo C ir jis pateikia per didelį atsakymą, galite išbraukti visus didesnius nei C atsakymų pasirinkimus, nes jie tikrai nebus teisingi.
b+ medis
Štai pavyzdys:

Pradėsime nuo C, kur y +z = 0.
Antroje lygtyje turime (y+z), todėl pakeisime ją ten.
3x+y+z=14
3x+0=14
3x=14
Dabar paimkite šią reikšmę 3 kartus ir pakeiskite ją pirmoje lygtyje. (Nereikia rasti vien x reikšmės (4,67), nes 3x kartojasi viršutinėje lygtyje.)
3x+2(y+z)=19
(Kodėl 2y+2z perrašėme kaip 2(y+z)? Nes galėjome paskirstyti bendrąjį 2 ir išlaikyti y+z nepažeistą)
14+2(0)=14
14≠19
Taigi C nėra teisinga.
Iš problemos galime ekstrapoliuoti, kad (y + z) nebus neigiamas. Kodėl? Kadangi 3x išlieka toks pat, bet sprendimas yra didesnis, kai (y + z) padvigubėja. Todėl (y + z) turi būti teigiamas, nes neigiamas (y + z) reikštų, kad viršutinė lygtis turės mažesnį nei apatinės lygties sprendinį.
Taigi toliau išbandykime D variantą.
3x+y+z=14
3x+4=14
3x = 10
Vėlgi, mums nereikia rasti individualios x reikšmės (3,33), nes 3x kartojasi viršutinėje lygtyje.
Taigi 3x+2(y+z)=19
10+2(4)=18
18≠19
Taigi D nėra teisinga.
Dabar pabandykime E variantą.
3x+y+z=14
3x+5=14
3x=9
Dabar šią vertę įtrauksime 3 kartus į viršutinę lygtį.
3x+2(y+z)=19
9+2(5)=19
19=19
reversinė eilutė java
Taigi mūsų galutinis atsakymas yra E, y+z=5.
# 14: pasirinkite vieną raidę visiems klausimams, kurių negalite išspręsti
Neretai pasitaiko keletas SAT matematikos klausimų, kurių tiesiog negalite išspręsti. Nenusiminkite dėl to! Tačiau tai, ką galite padaryti, yra maksimaliai padidinti galimybę gauti papildomų taškų, teisingai atspėdami problemas, kurių negalėjote išspręsti.
Geriausias būdas padidinti tikimybę atsitiktinai pasirinkti tinkamą atsakymą – pasirinkti raidę ir naudoti ją atsakant į visus klausimus, kuriuos spėjate. Tai gali būti bet kokia raidė A–D (nepaisant to, ką galbūt girdėjote, C nėra labiausiai paplitęs teisingas atsakymas ), tiesiog įsitikinkite, kad naudojate ją visiems atspėtiems klausimams (po to, kai pašalinsite visus akivaizdžiai neteisingus atsakymus).
Naudodami tik vieną raidę atspėti suteikiate 25 % tikimybę, kad kiekvienas klausimas bus teisingas, o jei atsitiktinai atspėjote kitą raidę, bendra tikimybė atspėti teisingai būtų žymiai mažesnė.

SAT matematikos gudrybės tinklelio klausimams
Pasinaudokite šiais SAT patarimais ir gudrybėmis, skirtomis matematiniams tinklelio klausimams, į kuriuos jums nėra duotas atsakymų pasirinkimas.
Nr. 15: žinokite, kaip užpildyti atsakymus į tinklelio klausimus
Norėdami atsakyti į klausimus apie SAT Math tinklelį, turite atlikti šiek tiek daugiau darbo nei tiesiog užpildyti tinkamą debesėlį. Neteisingai įvedę atsakymą į atsakymų lapą, galite prarasti daug taškų, net jei iš tikrųjų teisingai sprendžiate problemas. Štai taisyklės, kaip atsakyti į klausimus į tinklelį:#16: Papildinių numeriai problemoms spręsti
Jei kyla problemų dėl tinklelio, neturėsite galimų atsakymų į papildinį, kaip tai darote atsakydami į klausimus su atsakymų variantais. Tačiau galite įtraukti pasirinktas vertes, kad būtų lengviau išspręsti kai kuriuos iš šių klausimų.
Štai pavyzdys:

Kadangi mums nesakoma, kad ši problema tinka „visiems skaičiams“, žinome, kad turime pasirinkti savo skaičių tik vienam kintamajam ir išspręsti likusius.
Šioje užduotyje v pakeičiame savo skaičiumi. Kodėl v? Kadangi v rodomas vidurinėje lygtyje, tai bus naudinga ieškant kitų mūsų kintamųjų.
Taip pat matome, kad v=4t, taigi, duokime v skaičių, kuris dalijasi iš 4. (Pastaba: mes NEPRIVALome v dalytis iš 4, bet tai palengvina mūsų gyvenimą, nes tai reiškia, kad turėsime reikalų sveikieji skaičiai, o ne dešimtainės dalys.)
Taigi sakykime, kad v=8. Jei kiekvieną v pakeisime skaičiumi 8, mūsų pirmoji lygtis atrodytų taip:
x=3v
x=3(8)
x = 24
Taigi dabar žinome, kad kai v = 8, x = 24. Dabar mūsų antroji lygtis:
v=4t
8=4t
t=2
Taigi, kai x = 24 ir v = 8, t bus 2.
Ir galiausiai, pažvelkime į paskutinę lygtį, naudodami naujai rastus x ir t skaičius.
x=pt
24=p(2)
p=12
Taigi p lygus 12.
Bet palauk! Galbūt manote, kad p yra lygus 12 tik šiuo atveju ir kad jis būtų lygus kažkam kitam, jei pasirinktume kitą skaičių v. Na, išbandykime.
Tarkime, kad v = 20, o ne 8.
x=3v
x=3(20)
x=60
Ir mūsų antroji lygtis:
v=4t
20=4t
t=5
Ir galiausiai mūsų paskutinė lygtis:
x=pt
60=p(5)
p=12
Kaip matote, nesvarbu, kokią reikšmę pasirinktume vienam iš mūsų kintamųjų, p visada bus lygus 12, jei išliksime nepažeisti santykiai tarp kintamųjų.
Taigi mūsų galutinis atsakymas yra p=12.
Santrauka: SAT matematikos patarimai ir gudrybės
Gauti norimą rezultatą dažnai įmanoma, jei žinote pagrindinius SAT matematikos patarimus ir gudrybes. Čia yra mūsų 16 geriausių SAT matematikos gudrybių santrauka.
Nr. 1: Žinokite, kokia matematika būsite tikrinama Nr. 2: įsiminkite įprastas formules ir matematikos faktus Nr. 3: atlikite aukštos kokybės praktinius testus Nr. 4: mokykitės iš savo klaidų Nr. 5: Pakartokite klausimus, kuriuos suklydote prieš žiūrėdami į atsakymą Paaiškinimas Nr. 6: sutelkite dėmesį į savo studijas tose srityse, kuriose jums sunkiausia 7: Pabrėžkite pagrindines 8 klausimo dalis: Žinokite savo laiką Nr. 9: Įsitikinkite, kad išsprendėte teisingą vertę Nr. 10: Parodykite savo darbą Nr. 11 : Žinokite, kada padėti skaičiuotuvą # 12: pašalinkite 3 neteisingus atsakymus # 13: Papildiniai atsakymai, kad išspręstumėte problemas # 14: Pasirinkite vieną raidę visiems klausimams, kurių negalite išspręsti # 15: Žinokite, kaip užpildyti atsakymus 16 tinklelio klausimams: Papildinių numeriai problemoms spręstiKas toliau?
Bandote pagerinti savo SAT matematikos balą naudodami papildomus SAT matematikos patarimus ir gudrybes? Štai 9 SAT matematikos patarimai, skirti žmonėms, norintiems greitai padidinti SAT matematikos balą!
Ieškote knygų rekomendacijų, susijusių su matematikos skyriumi? Štai mūsų pasiūlymai dėl geriausių SAT Math paruošiamųjų knygų ir keletas patarimų, kaip jas efektyviausiai naudoti.
Norite įsitikinti, kad gerai išmanote matematikos pagrindus prieš pasinerdami į SAT matematiką? Peržiūrėkite mūsų atnaujinimo straipsnius apie sprendžiant nelygybes , trupmenų pridėjimas ir atėmimas , daugyba, tobuli kvadratai ir paskirstymo savybė .

