Prizmė yra trimatė vientisa figūra su dviem vienodais galais. Jis sudarytas iš plokščių kraštų, panašių pagrindų ir vienodo skerspjūvio. Jo paviršiai yra lygiagrečiai arba stačiakampiai be pagrindo. Tokia prizmė, turinti tris stačiakampius paviršius ir du lygiagrečius trikampio pagrindus, vadinama trikampe prizme. Trikampiai pagrindai yra sujungti šoniniais paviršiais, kurie yra lygiagrečiai vienas kitam.

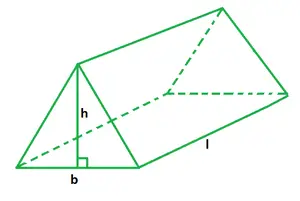
Trikampės prizmės formulės tūris

Trikampės prizmės tūris apibrėžiamas kaip erdvė jos viduje arba jos užpildyta erdvė. Norint apskaičiuoti jos tūrį, reikia žinoti trikampės prizmės pagrindo plotą ir aukštį. Trikampės prizmės tūris yra lygus pagrindo ploto ir prizmės aukščio sandaugai, taip pat žinomai kaip prizmės ilgis. Trikampės prizmės pagrindo plotas lygus pusei trikampio pagrindo ir jos aukščio sandaugos.

Formulė

V = (1/2) × b × h × l

kur,

b yra trikampis pagrindas,

h yra prizmės aukštis,

l yra prizmės ilgis.

Pavyzdinės problemos

1 uždavinys. Raskite trikampės prizmės tūrį, jei jos pagrindas yra 6 cm, aukštis virš jūros lygio 8 cm, o ilgis - 12 cm.

Sprendimas:

Turime b = 6, h = 8 ir l = 12.

mysql liko prisijungti

Naudodami mūsų turimą formulę,

V = (1/2) × b × h × l

= (1/2) × 6 × 8 × 12

= 3 × 8 × 12

= 288 kub. cm

vardas

2 uždavinys. Raskite trikampės prizmės tūrį, jei jos pagrindas yra 5 cm, aukštis virš jūros lygio – 7 cm, o ilgis – 8 cm.

Sprendimas:

Turime b = 5, h = 7 ir l = 8.

Naudodami mūsų turimą formulę,

V = (1/2) × b × h × l

= (1/2) × 5 × 7 × 8

= 5 × 7 × 4

= 140 kub. cm

3 uždavinys. Raskite trikampės prizmės ilgį, jei jos pagrindas yra 6 cm, aukštis virš jūros lygio 9 cm, o tūris – 98 kub. cm.

Sprendimas:

Turime b = 6, h = 9 ir V = 98.

Naudodami mūsų turimą formulę,

V = (1/2) × b × h × l

=> 98 = (1/2) × 6 × 9 × l

testavimas ir testavimo tipai

=> 196 = 27 l

=> l = 196/27

=> l = 7,25 cm

4 uždavinys. Raskite trikampės prizmės aukštį, jei jos pagrindas yra 8 cm, ilgis 14 cm, o tūris – 504 kub. cm.

Sprendimas:

Turime b = 8, l = 14 ir V = 504.

Naudodami mūsų turimą formulę,

V = (1/2) × b × h × l

=> 504 = (1/2) × 8 × h × 14

=> 504 = 56 val

=> h = 504/56

=> h = 9 cm

5 uždavinys. Raskite trikampės prizmės pagrindo plotą, jei jos ilgis 18 cm, aukštis 10 cm, tūris 450 kub. cm.

Sprendimas:

Turime l = 18, h = 10 ir V = 450.

Naudodami tūrio formulę turime,

V = (1/2) × b × h × l

=> 450 = (1/2) × b × 10 × 18

=> 450 = 90b

=> b = 450/90

sklearn tikslumo balas

=> b = 5 cm

Taigi trikampio pagrindo plotas yra

A = (1/2) × b × h

= (1/2) × 5 × 10

= 25 kv. cm