Šiame straipsnyje aptarsime medžio perėjimą duomenų struktūroje. Sąvoka „medžio perėjimas“ reiškia kiekvieno medžio mazgo perėjimą arba aplankymą. Yra vienas būdas pereiti tiesinę duomenų struktūrą, pvz., susietą sąrašą, eilę ir krūvą. Tuo tarpu yra keli būdai, kaip pereiti medį, kurie išvardyti taip:
- Išankstinis pervažiavimas
- Užsakymo perėjimas
- Pašto siuntų pervežimas
Taigi, šiame straipsnyje aptarsime aukščiau išvardintus medžio kirtimo būdus. Dabar pradėkime aptarti medžių perėjimo būdus.
Išankstinis pervažiavimas
Ši technika atitinka „šakninės kairės dešinės“ politiką. Tai reiškia, kad aplankomas pirmasis šakninis mazgas, po to kairysis pomedis perkeliamas rekursyviai, o galiausiai – rekursyviai perkeliamas dešinysis pomedis. Kadangi šakninis mazgas kertamas prieš (arba prieš) kairįjį ir dešinįjį pomedį, jis vadinamas išankstinio užsakymo perėjimu.
Taigi, atliekant išankstinį užsakymą, kiekvienas mazgas aplankomas prieš abu jo pomedžius.
Išankstinio užsakymo judėjimo programos apima:
- Jis naudojamas medžio kopijai sukurti.
- Jis taip pat gali būti naudojamas norint gauti išraiškos medžio priešdėlio išraišką.
Algoritmas
Until all nodes of the tree are not visited Step 1 - Visit the root node Step 2 - Traverse the left subtree recursively. Step 3 - Traverse the right subtree recursively.
Pavyzdys
Dabar pažiūrėkime išankstinio užsakymo perėjimo technikos pavyzdį.
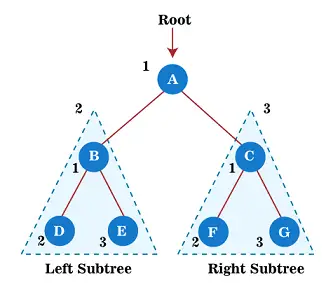
Dabar pradėkite taikyti išankstinio užsakymo judėjimą aukščiau esančiame medyje. Pirmiausia pereiname šakninį mazgą A; po to pereikite prie jo kairiojo pomedžio B , kuris taip pat bus perkeltas pagal išankstinį užsakymą.
Taigi, kairiajam pomedžiui B, pirma, šakninis mazgas B yra perkeliamas pats; po to jo kairysis pomedis D yra pravažiuojama. Nuo mazgo D neturi vaikų, pereiti į dešinįjį pomedį IR . Kadangi mazgas E taip pat neturi vaikų, šakninio mazgo A kairiojo pomedžio perėjimas baigtas.
git push komanda
Dabar eikite link šakninio mazgo A dešiniojo pomedžio, kuris yra C. Taigi dešiniajame pomedžiui C pirmiausia šakninis mazgas C perėjo save; po to jo kairysis pomedis F yra pravažiuojama. Nuo mazgo F neturi vaikų, pereikite prie dešiniojo pomedžio G . Kadangi mazgas G taip pat neturi vaikų, šakninio mazgo A dešiniojo pomedžio perėjimas baigtas.
Todėl visi medžio mazgai yra perkeliami. Taigi, pirmiau pateikto medžio išankstinio užsakymo perėjimo išvestis yra -
A → B → D → E → C → F → G
npm diegimo komanda
Norėdami sužinoti daugiau apie išankstinio užsakymo perėjimą duomenų struktūroje, galite spustelėti nuorodą Išankstinis pervažiavimas .
Pašto siuntų pervežimas
Šis metodas atitinka „kairės ir dešinės šaknies“ politiką. Tai reiškia, kad kertamas pirmasis kairysis šakninio mazgo pomedis, po to rekursyviai kerta dešinįjį pomedį ir galiausiai perkeliamas šakninis mazgas. Kadangi šakninis mazgas kertamas po kairiojo ir dešiniojo pomedžio (arba po jo), tai vadinama postorder traversal.
Taigi, atliekant postorder perėjimą, kiekvienas mazgas aplankomas po abiejų jo pomedžių.
Postorder traverzavimo programos apima:
- Jis naudojamas medžiui ištrinti.
- Jis taip pat gali būti naudojamas norint gauti išraiškos medžio postfix išraišką.
Algoritmas
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Traverse the right subtree recursively. Step 3 - Visit the root node.
Pavyzdys
Dabar pažiūrėkime apie postorder traversal technikos pavyzdį.

Dabar pradėkite taikyti postorder traversal ant aukščiau esančio medžio. Pirmiausia pereiname kairįjį pomedį B, kuris bus perkeliamas postorder. Po to pereisime dešiniuoju pomedžiu C pašte. Ir galiausiai aukščiau minėto medžio šaknies mazgas, t.y. A , yra pravažiuojama.
Taigi, kairiajam pomedžiui B, pirma, jo kairysis pomedis D yra pravažiuojama. Nuo mazgo D neturi vaikų, pereikite per dešinįjį pomedį IR . Kadangi mazgas E taip pat neturi vaikų, pereikite prie šakninio mazgo B. Pervažiavus mazgą B, baigiamas šakninio mazgo A kairiojo pomedžio perėjimas.
Dabar eikite link šaknies mazgo A dešiniojo pomedžio, kuris yra C. Taigi, dešiniajam pomedžiui C, pirmiausia jo kairysis pomedis F yra pravažiuojama. Nuo mazgo F neturi vaikų, pereikite per dešinįjį pomedį G . Kadangi mazgas G taip pat neturi vaikų, todėl galiausiai dešiniojo pomedžio šakninis mazgas, t.y. C, yra pravažiuojama. Baigtas šakninio mazgo A dešiniojo pomedžio perėjimas.
Pagaliau pereikite per tam tikro medžio šaknies mazgą, t.y. A . Perėjus šaknies mazgą, baigiamas duoto medžio postorder perėjimas.
Todėl visi medžio mazgai yra perkeliami. Taigi, aukščiau pateikto medžio postorder perėjimo išvestis yra -
D → E → B → F → G → C → A
Norėdami sužinoti daugiau apie postorder perėjimą duomenų struktūroje, galite spustelėti nuorodą Pašto siuntų pervežimas .
Užsakymo perėjimas
Šis metodas atitinka „kairiosios šaknies dešinės“ politiką. Tai reiškia, kad po to šakninio mazgo aplankomas pirmasis kairysis pomedis, o galiausiai – dešinysis pomedis. Kadangi šakninis mazgas kertamas tarp kairiojo ir dešiniojo pomedžio, jis vadinamas inorder traversal.
Taigi, eilės eilės metu kiekvienas mazgas aplankomas tarp jo pomedžių.
Inorder traversal programos apima:
išanalizuoti eilutę į int
- Jis naudojamas norint gauti BST mazgus didėjančia tvarka.
- Jis taip pat gali būti naudojamas norint gauti išraiškos medžio priešdėlio išraišką.
Algoritmas
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Visit the root node. Step 3 - Traverse the right subtree recursively.
Pavyzdys
Dabar pažiūrėkime Inorder traversal technikos pavyzdį.

Dabar pradėkite taikyti inorder traversal aukščiau esančiame medyje. Pirmiausia pereiname kairįjį pomedį B kad bus pereinama eilės tvarka. Po to pereisime šakninį mazgą A . Ir galiausiai, tinkamas pomedis C pereinama eilės tvarka.
Taigi, kairiajam pomedžiui B , pirma, jo kairysis pomedis D yra pravažiuojama. Nuo mazgo D vaikų neturi, todėl pervažiavus jį mazgas B bus pereita ir pagaliau dešinysis mazgo B pomedis, tai yra IR , yra pravažiuojama. Mazgas E taip pat neturi vaikų; todėl šakninio mazgo A kairiojo pomedžio perėjimas baigtas.
Po to pereikite per tam tikro medžio šaknies mazgą, t.y. A .
Galiausiai pereikite link šaknies mazgo A dešiniojo pomedžio, kuris yra C. Taigi, dešiniajam pomedžiui C; pirma, jo kairysis pomedis F yra pravažiuojama. Nuo mazgo F vaikų neturi, mazgas C bus pereita ir pagaliau dešinysis mazgo C pomedis, tai yra, G , yra pravažiuojama. Mazgas G taip pat neturi vaikų; todėl šakninio mazgo A dešiniojo pomedžio perėjimas baigtas.
Kadangi visi medžio mazgai yra perkeliami, duoto medžio eilė yra baigta. Aukščiau pateikto medžio eilės eilės išvestis yra -
D → B → E → A → F → C → G
Kaip atsisiųsti video iš youtube vlc
Norėdami sužinoti daugiau apie eilės eiliškumą duomenų struktūroje, galite spustelėti nuorodą Inorder Traversal .
Medžių perėjimo metodų sudėtingumas
Aukščiau aptartų medžių perėjimo metodų sudėtingumas laike yra O(n) , kur 'n' yra dvejetainio medžio dydis.
Tuo tarpu aukščiau aptartų medžių perėjimo metodų erdvės sudėtingumas yra toks O(1) jei neatsižvelgsime į funkcijų iškvietimų kamino dydį. Priešingu atveju šie metodai yra sudėtingi Oi) , kur 'h' yra medžio aukštis.
Tree traversal įgyvendinimas
Dabar pažiūrėkime, kaip įgyvendinamos aukščiau aptartos technikos naudojant skirtingas programavimo kalbas.
Programa: Parašykite programą, skirtą medžių perėjimo metodams įgyvendinti C.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(36); root->left = createNode(26); root->right = createNode(46); root->left->left = createNode(21); root->left->right = createNode(31); root->left->left->left = createNode(11); root->left->left->right = createNode(24); root->right->left = createNode(41); root->right->right = createNode(56); root->right->right->left = createNode(51); root->right->right->right = createNode(66); printf('
The Preorder traversal of given binary tree is -
'); traversePreorder(root); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); printf('
The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } Išvestis

Programa: Parašykite programą, kuri įgyvendintų medžio apėjimo metodus C#.
using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Preorder traversal of given binary tree is - '); bt.traversePreorder(); Console.WriteLine(); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); Console.WriteLine(); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } Išvestis

Programa: Parašykite programą, skirtą medžių perėjimo technikoms įgyvendinti C++.
perjungti java programavimą
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout<<' '<element<left); traversepreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } *function to traverse the nodes of binary tree in postorder* void traversepostorder(struct node* root) { if (root="=" null) return; traversepostorder(root->left); traversePostorder(root->right); cout<<' '<element<left="createNode(28);" root->right = createNode(48); root->left->left = createNode(23); root->left->right = createNode(33); root->left->left->left = createNode(13); root->left->left->right = createNode(26); root->right->left = createNode(43); root->right->right = createNode(58); root->right->right->left = createNode(53); root->right->right->right = createNode(68); cout<<'
the preorder traversal of given binary tree is -
'; traversepreorder(root); cout<<'
inorder traverseinorder(root); postorder traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-6.webp" alt="Tree Traversal"> <p> <strong>Program:</strong> Write a program to implement tree traversal techniques in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class Tree { Node root; /* root of the tree */ Tree() { root = null; } /*function to print the nodes of given binary in Preorder*/ void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } /*function to print the nodes of given binary in Inorder*/ void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } /*function to print the nodes of given binary in Postorder*/ void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { Tree pt = new Tree(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println('
'); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println('
'); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-7.webp" alt="Tree Traversal"> <h2>Conclusion</h2> <p>In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.</p> <p>So, that's all about the article. Hope it will be helpful and informative to you.</p> <hr></'
></'></'></'> Išvestis
Įvykdžius aukščiau pateiktą kodą, išvestis bus -

Išvada
Šiame straipsnyje aptarėme įvairius medžių perėjimo metodus: išankstinio užsakymo perėjimą, įsakymo perėjimą ir postorder perėjimą. Mes matėme šiuos metodus kartu su algoritmu, pavyzdžiu, sudėtingumu ir įgyvendinimu C, C++, C# ir Java.
Taigi, viskas apie straipsnį. Tikimės, kad tai bus naudinga ir informatyvi.
