Šiame straipsnyje aptarsime eilės eiliškumą duomenų struktūroje.
Jei norime pereiti mazgus didėjančia tvarka, tada naudojame inorder traversal. Toliau pateikiami žingsniai, reikalingi norint pereiti į eilutę:
- Aplankykite visus kairiojo pomedžio mazgus
- Apsilankykite šakniniame mazge
- Aplankykite visus dešiniojo pomedžio mazgus
Linijinės duomenų struktūros, tokios kaip dėklas, masyvas, eilė ir t. t., turi tik vieną būdą perduoti duomenis. Tačiau hierarchinėse duomenų struktūrose, pvz medis, yra keletas būdų, kaip perkelti duomenis. Čia aptarsime kitą būdą, kaip pereiti medžio duomenų struktūrą, t.
Yra du būdai, kaip pereiti į eilutę:
- Užsakyti perėjimą naudojant Recursion
- Inorder perėjimas naudojant iteracinį metodą
Taikoma inorder traversal technika Kairė šaknis dešinė politika. Čia Left Root Right reiškia, kad pirmiausia perkeliamas kairysis šakninio mazgo pomedis, tada šakninis mazgas ir tada dešinysis šakninio mazgo pomedis. Čia pats eilės pavadinimas rodo, kad šakninis mazgas yra tarp kairiojo ir dešiniojo pomedžio.
Aptarsime eilės eiliškumą naudodami rekursinius ir iteracinius metodus. Pirmiausia pradėkime nuo eilės perėjimo naudojant rekursiją.
Inorder perėjimas naudojant rekursiją
Step 1: Recursively traverse the left subtree Step 2: Now, visit the root Step 3: Traverse the right subtree recursively
Inorder perėjimo pavyzdys
Dabar pažiūrėkime į eilės tvarką pavyzdį. Naudojant pavyzdį, bus lengviau suprasti įprastos eilės perėjimo procedūrą.
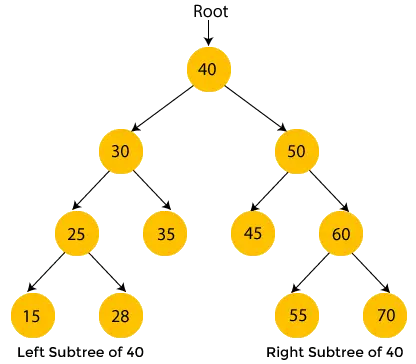
Geltonos spalvos mazgai dar nelankyti. Dabar pereisime aukščiau pateikto medžio mazgus naudodami inorder traversal.
- Čia 40 yra šakninis mazgas. Perkeliame į kairįjį 40 pomedį, tai yra 30, ir jame taip pat yra 25 pomedis, todėl vėl pereiname prie kairiojo 25 pomedžio, kuris yra 15. Čia 15 pomedžio nėra, taigi spausdinti 15 ir pereikite link pirminio mazgo 25.
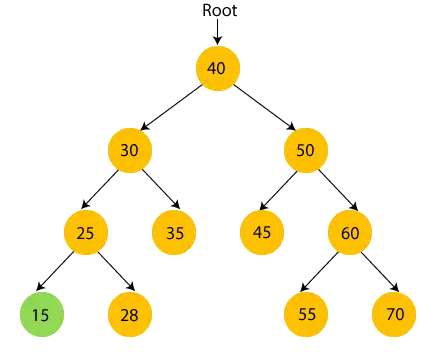
- Dabar spausdinti 25 ir pereikite į dešinįjį 25 pomedį.
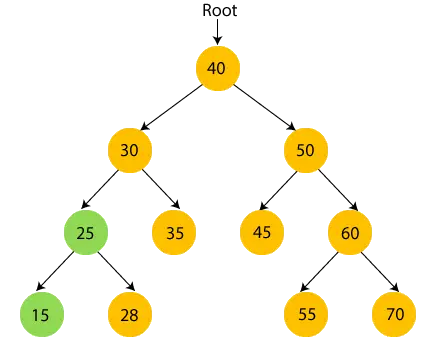
- Dabar spausdinti 28 ir pereikite prie šakninio mazgo 25, tai yra 30.
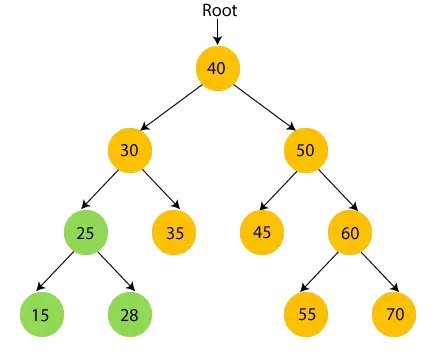
- Taigi, lankomas kairysis 30 pomedis. Dabar spausdinti 30 ir pereiti pas dešinįjį 30 metų vaiką.
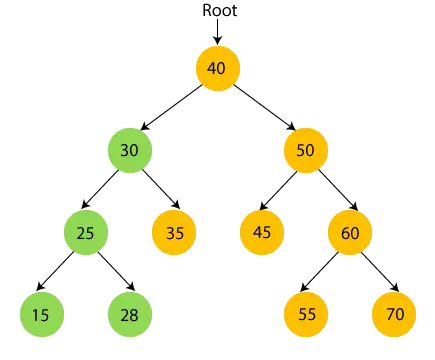
- Dabar spausdinti 35 ir pereikite prie 30 šakninio mazgo.
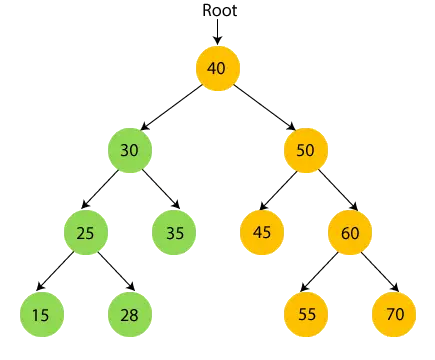
- Dabar spausdinti šakninį mazgą 40 ir pereikite prie jo dešiniojo pomedžio.
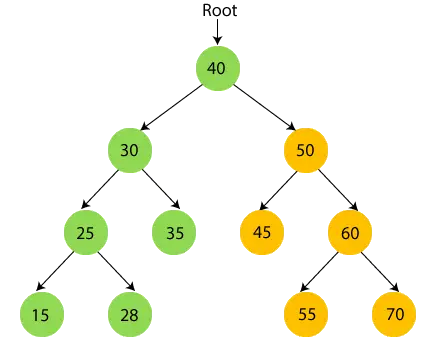
- Dabar rekursyviai pereikite dešinįjį 40 pomedį, kuris yra 50.
50 turi pomedį, todėl pirmiausia pereikite per kairįjį 50 pomedį, kuris yra 45. 45 neturi vaikų, todėl Spausdinti 45 ir pereiti į jo šakninį mazgą.
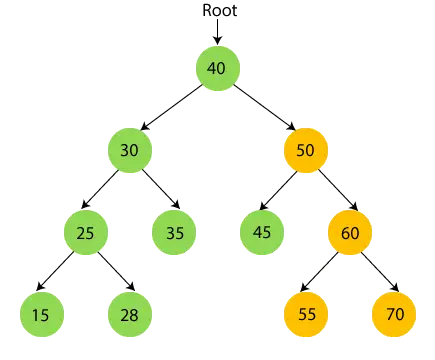
- Dabar spausdinti 50 ir pereikite prie dešiniojo 50 pomedžio, kuris yra 60.
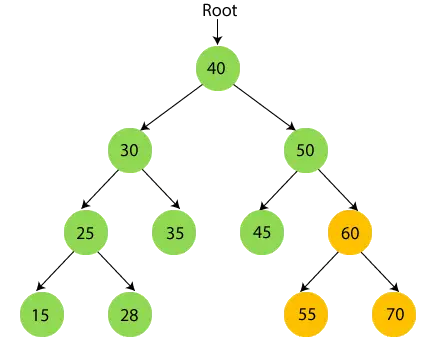
- Dabar rekursyviai pereikite dešinįjį 50 pomedį, kuris yra 60. 60 turi pomedį, taigi pirmiausia pereikite per kairįjį 60 pomedį, kuris yra 55. 55 neturi vaikų, taigi spausdinti 55 ir pereiti į jo šakninį mazgą.
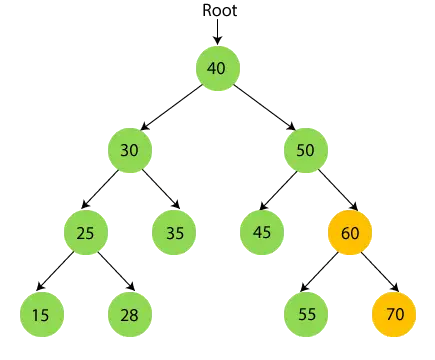
- Dabar spausdinti 60 ir pereikite prie dešiniojo pomedžio 60, tai yra 70.
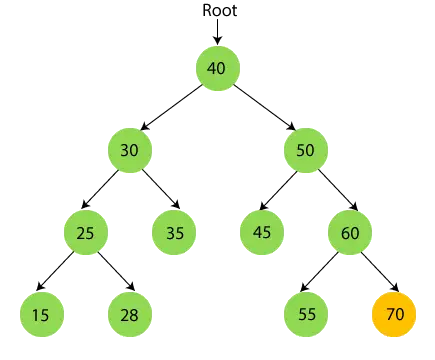
- Dabar spausdinti 70.
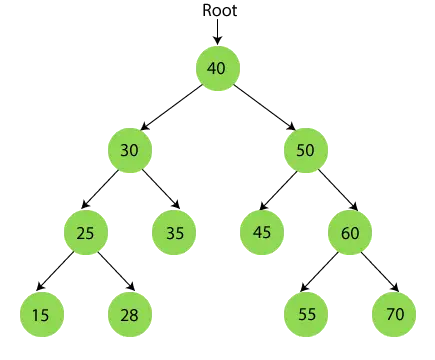
Užbaigus eilės tvarką, galutinis rezultatas yra -
{15, 25, 28, 30, 35, 40, 45, 50, 55, 60, 70}
Inorder perėjimo sudėtingumas
Inorder perėjimo laiko sudėtingumas yra O(n), kur „n“ yra dvejetainio medžio dydis.
java eilutė į int
Tuo tarpu erdvės sudėtingumas tarp eiliškumo yra toks O(1), jei neatsižvelgsime į funkcijų iškvietimų kamino dydį. Priešingu atveju, erdvės sudėtingumas inorder traverza yra Oi), kur „h“ yra medžio aukštis.
Inorder traversal įgyvendinimas
Dabar pažiūrėkime, kaip įgyvendinamas inorder traversal įvairiose programavimo kalbose.
Programa: Parašykite programą, kuri įgyvendintų inorder traversal C kalba.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } int main() { struct node* root = createNode(40); root->left = createNode(30); root->right = createNode(50); root->left->left = createNode(25); root->left->right = createNode(35); root->left->left->left = createNode(15); root->left->left->right = createNode(28); root->right->left = createNode(45); root->right->right = createNode(60); root->right->right->left = createNode(55); root->right->right->right = createNode(70); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); return 0; } Išvestis

Programa: Parašykite programą, kuri įgyvendintų inorder traversal C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } int main() { struct node* root="createNode(39);" root->left = createNode(29); root->right = createNode(49); root->left->left = createNode(24); root->left->right = createNode(34); root->left->left->left = createNode(14); root->left->left->right = createNode(27); root->right->left = createNode(44); root->right->right = createNode(59); root->right->right->left = createNode(54); root->right->right->right = createNode(69); cout<<'
the inorder traversal of given binary tree is -
'; traverseinorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-14.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in C#.</p> <pre> using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(36); bt.root.left = new Node(26); bt.root.right = new Node(46); bt.root.left.left = new Node(21); bt.root.left.right = new Node(31); bt.root.left.left.left = new Node(11); bt.root.left.left.right = new Node(24); bt.root.right.left = new Node(41); bt.root.right.right = new Node(56); bt.root.right.right.left = new Node(51); bt.root.right.right.right = new Node(66); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-15.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-16.webp" alt="Inorder Traversal"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></'
></'> Išvestis

Programa: Parašykite programą, kuri įdiegtų inorder traversal Java.
class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } Išvestis

Taigi, viskas apie straipsnį. Tikimės, kad straipsnis bus jums naudingas ir informatyvus.











