Topologinis rūšiavimas Režisuotas aciklinis grafikas (DAG) yra tiesinė viršūnių tvarka, kad kiekviena nukreipta briauna u-v būtų viršūnė in ateina anksčiau in užsakyme.
Pastaba: Topologinis grafiko rūšiavimas neįmanomas, jei grafikas nėra a DIENA .
Pavyzdys:
Rekomenduojama praktikaDFS pagrįstas sprendimas topologiniam rūšiavimui rasti jau buvo aptarta.Įvestis: Grafikas:
Pavyzdys
Išvestis: 5 4 2 3 1 0
Paaiškinimas: Pirmoji topologinio rūšiavimo viršūnė visada yra viršūnė, kurios laipsnis yra 0 (viršūnė be įeinančių briaunų). Topologinis šio grafiko rūšiavimas yra 5 4 2 3 1 0. Grafui gali būti daugiau nei vienas topologinis rūšiavimas. Kitas šio grafiko topologinis rūšiavimas yra 4 5 2 3 1 0.
Topologinė tvarka negali būti unikali:
Topologinis rūšiavimas yra priklausomybės problema, kai vienos užduoties atlikimas priklauso nuo kelių kitų užduočių, kurių tvarka gali skirtis, atlikimo. Supraskime šią sąvoką pavyzdžiu:
Tarkime, kad mūsų užduotis yra pasiekti savo mokyklą ir, kad ją pasiektume, pirmiausia turime apsirengti. Priklausomybės dėvėti drabužius parodytos toliau pateiktoje priklausomybės diagramoje. Pavyzdžiui, prieš dėvėdami kojines negalite avėti batų.
Iš aukščiau pateikto paveikslėlio jau supratote, kad yra keli apsirengimo būdai, žemiau esančiame paveikslėlyje parodyti kai kurie iš tų būdų.
json formato pavyzdysAr galite išvardyti visa įmanoma topologinė tvarka apsirengti pagal aukščiau pateiktą priklausomybės grafiką?
Topologinio rūšiavimo naudojant DFS algoritmas:
Štai žingsnis po žingsnio algoritmas topologiniam rūšiavimui naudojant pirmą gylio paiešką (DFS):
- Sukurkite grafiką su n viršūnių ir m - nukreipti kraštai.
- Inicijuoti krūvą ir aplankyto dydžio masyvą n .
- Kiekvienai neaplankytai grafiko viršūnei atlikite šiuos veiksmus:
- Iškvieskite DFS funkciją, kurios parametras yra viršūnė.
- DFS funkcijoje pažymėkite viršūnę kaip aplankytą ir rekursyviai iškvieskite DFS funkciją visoms nelankomoms viršūnės kaimynėms.
- Kai aplankysite visus kaimynus, stumkite viršūnę ant kamino.
- Juk buvo aplankytos viršūnės, iškelkite elementus iš krūvos ir pridėkite juos prie išvesties sąrašo, kol krūva bus tuščia.
- Gautas sąrašas yra topologiškai surūšiuota grafiko tvarka.
Iliustracijos topologinio rūšiavimo algoritmas:
Žemiau pateiktame paveikslėlyje pavaizduotas aukščiau pateiktas metodas:

Bendra topologinio rūšiavimo darbo eiga
1 žingsnis:
- DFS pradedame nuo 0 mazgo, nes jame nėra jokių gaunamų mazgų
- Mes įstumiame mazgą 0 į krūvą ir pereiname prie kito mazgo, turinčio minimalų gretimų mazgų skaičių, t. y. 1 mazgą.
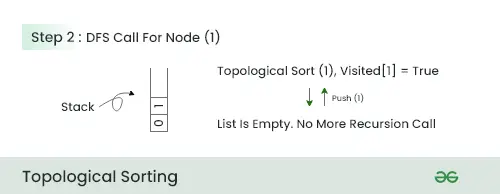
2 žingsnis:
- Šiame žingsnyje , kadangi šalia šio mazgo nėra, stumkite 1 mazgą į krūvą ir pereikite prie kito mazgo.
3 veiksmas:
- Šiame žingsnyje pasirenkame 2 mazgą, nes jame yra minimalus gretimų mazgų skaičius po 0 ir 1.
- Iškviečiame 2 mazgo DFS ir stumiame visus mazgus, kurie ateina iš 2 mazgo, atvirkštine tvarka.
- Taigi paspauskite 3, tada paspauskite 2.
4 veiksmas:
- Dabar vadiname DFS 4 mazgui
- Kadangi 0 ir 1 jau yra krūvoje, todėl mes tiesiog įstumiame 4 mazgą į krūvą ir grįžtame.
5 veiksmas:
- Šiame žingsnyje, kadangi visi gretimi 5 mazgai jau yra krūvoje, mes įstumiame 5 mazgą į krūvą ir grįžtame.
6 veiksmas: Tai paskutinis topologinio rūšiavimo žingsnis, kurio metu mes iškeliame visus elementus iš krūvos ir spausdiname tokia tvarka.
Toliau pateikiamas pirmiau minėto metodo įgyvendinimas:
C++ #include using namespace std; // Function to perform DFS and topological sorting void topologicalSortUtil(int v, vector>& adj, vektorius & aplankytas, sukrauti & Stack) { // Pažymėti dabartinį mazgą kaip aplankytą aplankytas[v] = true; // Pakartoti visoms gretimoms viršūnėms for (int i : adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Stack); } // Stumkite esamą viršūnę į krūvą, kurioje saugomas rezultatas Stack.push(v); } // Topologinio rūšiavimo funkcija void topologicalSort(vector>& adj, int V) { krūva Stack; // Stack, kad išsaugotumėte rezultatų vektorių aplankytas(V, false); // Iškvieskite rekursinio pagalbininko funkciją, kad išsaugotumėte // Topologinis rūšiavimas pradedant nuo visų viršūnių po vieną // po vieną (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Stack); } // Print contents of stack while (!Stack.empty()) { cout << Stack.top() << ' '; Stack.pop(); } } int main() { // Number of nodes int V = 4; // Edges vector> briaunos = { { 0, 1 }, { 1, 2 }, { 3, 1 }, { 3, 2 } }; // Grafas vaizduojamas kaip gretimų sąrašo vektorius> adj(V); for (auto i : briaunos) { adj[i[0]].push_back(i[1]); } cout<< 'Topological sorting of the graph: '; topologicalSort(adj, V); return 0; }>
Java import java.util.*; public class TopologicalSort { // Function to perform DFS and topological sorting static void topologicalSortUtil(int v, List> Adj, Boolean[] aplankė, Stack stack) { // Pažymėti dabartinį mazgą kaip aplankytą aplankytas[v] = true; // Pakartoti visoms gretimoms viršūnėms for (int i : adj.get(v)) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Stumkite esamą viršūnę į krūvą, kurioje saugomas // rezultatas stack.push(v); } // Funkcija topologiniam rūšiavimui atlikti statinį void topologicalSort(List> adj, int V) { // Stack, kad išsaugotumėte rezultatą Stack stack = naujas Stack(); loginis [] aplankytas = naujas loginis [V]; // Iškvieskite rekursinę pagalbinę funkciją, kad išsaugotumėte // Topologinis rūšiavimas pradedant nuo visų viršūnių po vieną // po vieną (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack System.out.print( 'Topological sorting of the graph: '); while (!stack.empty()) { System.out.print(stack.pop() + ' '); } } // Driver code public static void main(String[] args) { // Number of nodes int V = 4; // Edges List> briaunos = naujas ArrayList(); edges.add(Arrays.asList(0, 1)); edges.add(Arrays.asList(1, 2)); edges.add(Arrays.asList(3, 1)); edges.add(Arrays.asList(3, 2)); // Grafikas vaizduojamas kaip gretimų sąrašo sąrašas> adj = naujas ArrayList(V); už (int i = 0; i< V; i++) { adj.add(new ArrayList()); } for (List i : briaunos) { adj.get(i.get(0)).add(i.get(1)); } topologinis Rūšiuoti(adj, V); } }>>Python3
C# using System; using System.Collections.Generic; class Program { // Function to perform DFS and topological sorting static void TopologicalSortUtil(int v, List> adj, bool[] aplankė, Stack stack) { // Pažymėti dabartinį mazgą kaip aplankytą aplankytas[v] = true; // Recur visoms gretimoms viršūnėms foreach(int i in adj[v]) { if (!visited[i]) TopologicalSortUtil(i, adj, visited, stack); } // Stumkite esamą viršūnę į krūvą, kurioje saugomas // rezultatų krūvas. Push(v); } // Funkcija topologiniam rūšiavimui atlikti statinį void TopologicalSort(List> adj, int V) { // Stack, kad išsaugotumėte rezultatą Stack stack = naujas Stack (); bool[] aplankytas = naujas bool[V]; // Iškvieskite rekursinę pagalbinę funkciją, kad išsaugotumėte // Topologinis rūšiavimas pradedant nuo visų viršūnių po vieną // po vieną (int i = 0; i< V; i++) { if (!visited[i]) TopologicalSortUtil(i, adj, visited, stack); } // Print contents of stack Console.Write('Topological sorting of the graph: '); while (stack.Count>0) { Console.Write(stack.Pop() + ' '); } } // Tvarkyklės kodas static void Main(string[] args) { // Mazgų skaičius int V = 4; // Kraštų sąrašas> briaunos = naujas sąrašas>{ naujas sąrašas {0, 1}, naujas sąrašas { 1, 2 }, naujas sąrašas { 3, 1 }, naujas sąrašas {3, 2}}; // Grafikas vaizduojamas kaip gretimų sąrašo sąrašas> adj = naujas sąrašas>(); už (int i = 0; i< V; i++) { adj.Add(new List ()); } foreach(Sąrašas i briaunose) { adj[i[0]].Pridėti(i[1]); } TopologicalSort(adj, V); } }>>Javascript0) { console.log(stack.pop() + ' '); } } // Tvarkyklės kodas (() => { // Mazgų skaičius const V = 4; // Briaunos const briaunos = [[0, 1], [1, 2], [3, 1], [3, 2]] // Grafikas, vaizduojamas kaip gretimų sąrašas const adj = Masyvas.from({ ilgis: V }, () => [] for (tegu kraštų i) { adj[i[0]] (i[1]); } topologinis Rūšiuoti (adj, V })>>
Išvestis Topological sorting of the graph: 3 0 1 2>
Laiko sudėtingumas: O(V+E). Aukščiau pateiktas algoritmas yra tiesiog DFS su papildomu kaminu. Taigi laiko sudėtingumas yra toks pat kaip DFS
Pagalbinė erdvė: O(V). Kaminui reikia papildomos vietos
Topologinis rūšiavimas naudojant BFS:
C++ #include #include #include using namespace std; // Class to represent a graph class Graph { int V; // No. of vertices list * adj; // Rodyklė į masyvą, kuriame yra // gretimų sąrašai public: Graph(int V); // Konstruktorius void addEdge(int v, int w); // Funkcija pridėti briauną į grafiką void topologicalSort(); // atspausdina topologinį // viso grafiko tipą }; Grafikas::Grafas(int V) { this->V = V; adj = naujas sąrašas [V]; } void Grafas::addEdge(int v, int w) { adj[v].push_back(w); // Pridėkite w prie v sąrašo. } // Funkcija atlikti topologinį rūšiavimą void Graph::topologicalSort() { // Sukurkite vektorių, skirtą saugoti visų viršūnių vektorių laipsniu in_degree(V, 0); // Pereikite gretimų sąrašus, kad užpildytumėte viršūnių in_degree // (int v = 0; v< V; ++v) { for (auto const& w : adj[v]) in_degree[w]++; } // Create a queue and enqueue all vertices with // in-degree 0 queue q; už (int i = 0; i< V; ++i) { if (in_degree[i] == 0) q.push(i); } // Initialize count of visited vertices int count = 0; // Create a vector to store topological order vector top_order; // Po vieną iš eilės ir eilės ištraukiamos viršūnės // gretimos viršūnės, jei gretimo laipsnis tampa 0, while (!q.empty()) { // Išskleiskite eilės priekį (arba atlikite ištraukimą) // ir pridėkite prie topologinė tvarka int u = q.front(); q.pop(); top_order.push_back(u); // Pakartokite visus gretimus mazgus // iš ištraukto mazgo u ir sumažinkite jų laipsnį // 1 sąrašu ::iteratorius itr; for (itr = adj[u].begin(); itr != adj[u].end(); ++itr) // Jei laipsnis tampa nuliu, įtraukite jį į eilę if (--in_degree[*itr ] == 0) q.push(*itr); skaičiuoti++; } // Patikrinkite, ar buvo ciklas if (count != V) { cout<< 'Graph contains cycle
'; return; } // Print topological order for (int i : top_order) cout << i << ' '; } // Driver code int main() { // Create a graph given in the above diagram Graph g(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); cout << 'Following is a Topological Sort of the given ' 'graph
'; g.topologicalSort(); return 0; }> Java import java.util.ArrayList; import java.util.LinkedList; import java.util.Queue; // Class to represent a graph class Graph { private int V; // No. of vertices private ArrayList [] adj; // Gretumų sąrašas // grafiko // vaizdavimas // Konstruktoriaus grafikas(int V) { this.V = V; adj = naujas ArrayList[V]; už (int i = 0; i< V; ++i) adj[i] = new ArrayList(); } // Function to add an edge to the graph void addEdge(int v, int w) { adj[v].add(w); // Add w to v’s list. } // Function to perform Topological Sort void topologicalSort() { // Create an array to store in-degree of all // vertices int[] inDegree = new int[V]; // Calculate in-degree of each vertex for (int v = 0; v < V; ++v) { for (int w : adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with // in-degree 0 Queue q = naujas LinkedList(); už (int i = 0; i< V; ++i) { if (inDegree[i] == 0) q.add(i); } // Initialize count of visited vertices int count = 0; // Create an ArrayList to store topological order ArrayList topOrder = naujas ArrayList(); // Vieną po kitos iškelkite viršūnes iš eilės ir // į eilę gretimas viršūnes, jei // gretimų viršūnių laipsnis tampa 0 while (!q.isEmpty()) { // Išskleiskite eilės priekį ir įtraukite ją į // topologinę tvarką int u = q.poll(); topOrder.add(u); skaičiuoti++; // Pakartokite visus gretimus // ištraukto mazgo u mazgus ir sumažinkite jų laipsnį // 1 už (int w : adj[u]) { // Jei laipsnis tampa nuliu, įtraukite jį į // eilę if (--inDegree[w] == 0) q.add(w); } } // Patikrinkite, ar buvo ciklas if (count != V) { System.out.println('Grafoje yra ciklas'); grąžinti; } // Spausdinti topologinę tvarką (int i : topOrder) System.out.print(i + ' '); } } // Tvarkyklės kodas public class Main { public static void main(String[] args) { // Sukurkite grafiką, pateiktą aukščiau pateiktoje diagramoje Grafas g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); System.out.println('Toliau pateikiamas topologinis nurodyto grafiko rūšiavimas'); g.topologinis Rūšiuoti(); } }>>Python3 JavaScript // Class to represent a graph class Graph { constructor(V) { this.V = V; // No. of vertices this.adj = new Array(V); // Array containing adjacency lists for (let i = 0; i < V; i++) { this.adj[i] = []; } } // Function to add an edge to the graph addEdge(v, w) { this.adj[v].push(w); // Add w to v’s list. } // Function to perform Topological Sort topologicalSort() { // Create a array to store in-degree of all vertices let inDegree = new Array(this.V).fill(0); // Traverse adjacency lists to fill inDegree of vertices for (let v = 0; v < this.V; v++) { for (let w of this.adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with in-degree 0 let queue = []; for (let i = 0; i < this.V; i++) { if (inDegree[i] === 0) { queue.push(i); } } // Initialize count of visited vertices let count = 0; // Create an array to store topological order let topOrder = []; // One by one dequeue vertices from queue and enqueue // adjacent vertices if in-degree of adjacent becomes 0 while (queue.length !== 0) { // Extract front of queue and add it to topological order let u = queue.shift(); topOrder.push(u); // Iterate through all its neighboring nodes // of dequeued node u and decrease their in-degree by 1 for (let w of this.adj[u]) { // If in-degree becomes zero, add it to queue if (--inDegree[w] === 0) { queue.push(w); } } count++; } // Check if there was a cycle if (count !== this.V) { console.log('Graph contains cycle'); return; } // Print topological order console.log('Topological Sort of the given graph:'); console.log(topOrder.join(' ')); } } // Driver code // Create a graph given in the above diagram let g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); console.log('Following is a Topological Sort of the given graph:'); g.topologicalSort(); //This code is contributed by Utkarsh> Išvestis
Grafo konstravimo laiko sudėtingumas yra O(V + E), kur V – viršūnių skaičius, o E – briaunų skaičius.
Topologinio rūšiavimo naudojant BFS laiko sudėtingumas taip pat yra O(V + E), kur V yra viršūnių skaičius, o E yra briaunų skaičius. Taip yra todėl, kad kiekviena viršūnė ir kiekviena briauna aplankoma vieną kartą per BFS perėjimą.
Erdvės sudėtingumas:
Grafo saugojimo naudojant gretimų sąrašą erdvės sudėtingumas yra O(V + E), kur V yra viršūnių skaičius, o E yra briaunų skaičius.
Papildoma vieta naudojama viršūnių laipsnio saugojimui, o tam reikia O(V) vietos.
BFS perėjimui naudojama eilė, kurioje gali būti daugiausia V viršūnių. Taigi, eilės erdvės sudėtingumas yra O(V).
Šarvanandas
Apskritai algoritmo erdvės sudėtingumas yra O(V + E) dėl grafiko, laipsnio masyvo ir eilės saugojimo.
Apibendrinant galima pasakyti, kad pateikto įgyvendinimo laiko sudėtingumas yra O(V + E), o erdvės sudėtingumas taip pat yra O(V + E).
Pastaba: Čia taip pat galime naudoti masyvą vietoj krūvos. Jei naudojamas masyvas, atspausdinkite elementus atvirkštine tvarka, kad gautumėte topologinį rūšiavimą.
Topologinio rūšiavimo pranašumai:
- Padeda planuoti užduotis ar įvykius pagal priklausomybes.
- Aptinka ciklus nukreiptame grafike.
- Veiksmingas sprendžiant problemas su pirmumo apribojimais.
Topologinio rūšiavimo trūkumai:
- Taikoma tik nukreiptoms aciklinėms diagramoms (DAG), netinka ciklinėms diagramoms.
- Negali būti unikalus, gali būti keli galiojantys topologiniai išdėstymai.
- Neefektyvus dideliems grafams su daug mazgų ir kraštų.
Topologinio rūšiavimo programos:
- Užduočių planavimas ir projektų valdymas.
- Priklausomybės sprendimas paketų valdymo sistemose.
- Kompiliavimo tvarkos nustatymas programinės įrangos kūrimo sistemose.
- Aklavietės aptikimas operacinėse sistemose.
- Kursų planavimas universitetuose.
Susiję straipsniai:
- Kahno topologinio rūšiavimo algoritmas
- Visi topologiniai nukreipto aciklinio grafiko tipai