Trigonometrija yra svarbi matematikos šaka, nagrinėjanti stačiakampio trikampio kampų ir kraštinių ilgių ryšį. Šeši trigonometriniai santykiai arba funkcijos yra sinusas, kosinusas, liestinė, kosekantas ir sekantas, o trigonometrinis santykis yra santykis tarp stačiakampio trikampio kraštinių. Sinuso, kosinuso ir liestinės funkcijos yra trys svarbios trigonometrinės funkcijos, nes kitos trys, ty kosekantinės, sekantinės ir kotangentinės funkcijos yra atitinkamai sinuso, kosinuso ir liestinės funkcijos abipusės funkcijos.
- sin θ = priešinga pusė/hipotenuzė
- cos θ = gretima pusė/hipotenūza
- tan θ = priešinga pusė/gretima pusė
- cosec θ = hipotenuzė / priešinga pusė
- sek θ = hipotenuzė/gretima pusė
- lovelė θ = gretima pusė / priešinga pusė
Tangentinė funkcija yra viena iš 6 naudojamų trigonometrinių funkcijų trigonometrijos formulės .
Turinys
Tangento formulė
Stačiakampio trikampio kampo liestinė yra priešingos kraštinės ilgio ir gretimos kraštinės ilgio santykis su nurodytu kampu. Tangento funkciją rašome kaip tan. Panagrinėkime stačiakampį trikampį XYZ, kurio vienas smailių kampų yra θ. Priešinga pusė yra ta, kuri yra priešinga kampui θ, o gretima pusė yra ta, kuri yra greta kampo θ.
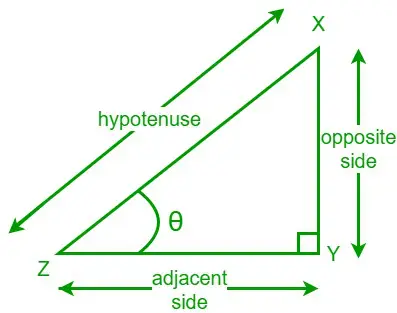
Dabar duoto kampo θ liestinės formulė yra
tan θ = priešinga pusė/gretima pusė
Kai kurios pagrindinės tangentų formulės
Tangentinė funkcija kvadrantuose
Tangento funkcija yra teigiama pirmame ir trečiame kvadrantuose, o neigiama antrajame ir ketvirtame kvadrantuose.
- įdegis (2π + θ) = įdegis θ (1Švkvadrantas)
- įdegis (π – θ) = – įdegis θ (2ndkvadrantas)
- įdegis (π + θ) = įdegis θ (3rdkvadrantas)
- įdegis (2π – θ) = – įdegis θ (4thkvadrantas)
Tangentinė funkcija kaip neigiama funkcija
Liestinės funkcija yra neigiama funkcija, nes neigiamo kampo liestinė yra liestinės teigiamo kampo neigiama.
tan (-θ) = – tan θ
Tangentinė funkcija sinusinės ir kosinusinės funkcijos požiūriu
Tangentinė funkcija sinuso ir kosinuso atžvilgiu gali būti parašyta kaip,
tan θ = sin θ/cos θ
Mes žinome, kad įdegis θ = priešinga pusė/gretima pusė
Dabar padalinkite skaitiklį ir vardiklį su hipotenuze
tan θ = (priešinga pusė/hipotenūza)/(gretima pusė/hipotenūza)
Mes žinome, kad sin θ = priešinga pusė / hipotenuzė
cos θ = gretima pusė/hipotenuzė
Vadinasi, tan θ = sin θ/cos θ
Tangentinė funkcija sinusinės funkcijos požiūriu
Tangentinė funkcija sinusinės funkcijos atžvilgiu gali būti parašyta kaip,
tan θ = sin θ/(√1 – sin 2 i)
Mes tai žinome,
tan θ = sin θ/cos θ
git status -s
Iš pitagoriečių tapatybių mes turime,
be2θ + cos2θ = 1
cos2θ = 1 – nuodėmė2i
cos θ = √(1 – sin2i)
Vadinasi, tan θ = sin θ/(√1 – nuodėmė2i)
Tangentinė funkcija kosinuso funkcijos požiūriu
Tangentinė funkcija, kalbant apie kosinuso funkciją, gali būti parašyta kaip,
tan θ = (√1 -cos 2 i)/cos i
Mes tai žinome,
tan θ = sin θ/cos θ
Iš pitagoriečių tapatybių mes turime,
be2θ + cos2θ = 1
be2θ = 1 – cos2i
sin θ = √(1 – cos2i)
Vadinasi, tan θ = (√1 – cos2i)/cos i
Tangentinė funkcija kotangentinės funkcijos požiūriu
Tangentinė funkcija, kalbant apie kotangentinę funkciją, gali būti parašyta kaip,
įdegis θ = 1/lovytė θ
arba
įdegis θ = vaikiška lovelė (90° – θ) (arba) lova (π/2 – θ)
Tangentinė funkcija kosekantinės funkcijos požiūriu
Tangentinė funkcija, kalbant apie kosekantinę funkciją, gali būti parašyta kaip,
įdegio θ = 1/√ (kosek 2 aš - 1)
Iš pitagoriečių tapatybių mes turime,
cosec2θ – vaikiška lovelė2θ = 1
vaikiška lovelė2θ = kosek2aš - 1
vaikiška lovelė θ = √ (kosek2aš - 1)
Mes tai žinome,
įdegio θ = 1/lovytė θ
Vadinasi, tan θ = 1/√ (kosek2aš - 1)
Tangentinė funkcija, kalbant apie sekantinę funkciją
Tangentinė funkcija, kalbant apie sekantinę funkciją, gali būti parašyta kaip,
tan θ = √sek 2 aš - 1
Iš pitagoriečių tapatybių mes turime,
sek2θ – taip2θ = 1
tan θ = sek2aš - 1
Vadinasi, tan θ = √ (sek2aš - 1)
Tangentinė funkcija dvigubo kampo požiūriu
Dvigubo kampo liestinės funkcija yra
tan 2θ = (2 tan θ)/(1 – tan 2 i)
Tangentinė funkcija trigubo kampo atžvilgiu
Trigubo kampo liestinės funkcija yra
tan 3θ = (3 tan θ – įdegis 3 θ) / (1–3 įdeg 2 i)
Liestinės funkcija pusės kampo atžvilgiu
Puskampio liestinės funkcija yra
įdegis (θ/2) = ± √[ (1 – cos θ) / (1 + cos θ) ]
tan (θ/2) = (1 – cos θ) / ( sin θ)
Liestinės funkcija dviejų kampų sudėjimo ir atėmimo terminais
Tangentinės funkcijos sumos ir skirtumo formulės yra
įdegis (A + B) = (įdegis A + įdegis B)/(1 – įdegis A įdegis B)
įdegis (A – B) = (įdegis A – įdegis B)/(1 + įdegis A įdegis B)
Trigonometrinių santykių lentelė
| Kampas (laipsniais) | Kampas (radianais) | nuodėmė i | cos θ | tan θ = sin θ/cos θ | cosec θ | sek θ | lovytė i |
|---|---|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0/1 = 0 | Neapibrėžtas | 1 | Neapibrėžtas |
| 30° | p/6 | 1/2 | √3/2 | (1/2)/(√3/2) = 1/√3 | 2 | 23 | √3 |
| 45° | p/4 | 1/√2 | 1/√2 | (1/√2)/(1/√2) = 1 | √2 | √2 | 1 |
| 60° | p/3 | √3/2 | 1/2 | (√3/2)/(1/2) = √3 sumažinimo vaizdas | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | 1/0 = neapibrėžta | 1 | Neapibrėžtas | 0 |
| 120° | 2p/3 | √3/2 | -1/2 | (√3/2)/(-1/2) = -√3 | 23 | -2 | -1/√3 |
| 150° | 5p/6 | 1/2 | -(√3/2) | (1/2)/(-√3/2) = -1/√3 | 2 | -(23) | -√3 |
| 180° | Pi | 0 | -1 | 0/(-1) = 0 | Neapibrėžtas | -1 | Neapibrėžtas |
Išspręstas liestinių formulių pavyzdys
1 pavyzdys: Raskite tan θ reikšmę, jei sin θ = 2/5 ir θ yra pirmasis kvadranto kampas.
Sprendimas:
Atsižvelgiant į
- sin θ = 2/5
Iš mūsų turimų pitagoriečių tapatybių,
be2θ + cos2θ = 1
cos2θ = 1 – nuodėmė2θ = 1 – (2/5)2
cos2θ = 1 – (4/5) = 21/25
cos θ = ±√21/5
Kadangi θ yra pirmasis kvadranto kampas, cos θ yra teigiamas.
cos θ = √21/5
Mes tai žinome,
tan θ = sin θ/cos θ
= (2/5)/(√21/5) = 2/√21
įdegio θ = 2√21 /21
Taigi, tan θ reikšmė, kai sin θ = 2/5 ir θ yra pirmame kvadrante, yra (2√21) /(21)
2 pavyzdys: Raskite tan x reikšmę, jei sek x = 13/12 ir x yra ketvirtasis kvadranto kampas.
Sprendimas:
Pateikta sek. x = 13/12
Iš pitagoriečių tapatybių mes turime,
sek2x – taip2x = 1
taip2x = sek2x – 1 = (13/12)2– 1
taip2x = (169/144) – 1 = 25/144
įdegis x = ± 5/12
Kadangi x yra ketvirtasis kvadranto kampas, tan x yra neigiamas.
įdegis x = – 5/12
Vadinasi, įdegis x = – 5/12
3 pavyzdys: jei tan X = 2/3 ir tan Y = 1/2, tai kokia yra tan reikšmė (X + Y)?
Sprendimas:
Atsižvelgiant į
įdegis X = 2/3 ir įdegis Y = 1/2
Mes tai žinome,
įdegis (X + Y) = (rusvai įdegis X + įdegis Y)/(1 – įdegis X įdegis Y)
įdegis (X + Y) = [(2/3) + (1/2)]/[1 – (2/3) × (1/2)]
mano gyvas kriketas= (7/6)/(2/3) = 7/4
Vadinasi, įdegis (X + Y) = 7/4
4 pavyzdys: Apskaičiuokite liestinės funkciją, jei gretimos ir priešingos stačiakampio trikampio kraštinės yra atitinkamai 4 cm ir 7 cm.
Sprendimas:
Atsižvelgiant į
Gretima pusė = 4 cm
Priešinga pusė = 7 cm
Mes tai žinome,
tan θ = priešinga pusė/gretima pusė
tan θ = 7/4 = 1,75
Vadinasi, tan θ = 1,75
5 pavyzdys: Vyras žiūri į laikrodžio bokštą 60° kampu į bokšto viršūnę, kurio aukštis yra 100 m. Koks atstumas tarp žmogaus ir bokšto papėdės?
Sprendimas:
Atsižvelgiant į
Bokšto aukštis = 100 m, o θ = 60°
Tegul atstumas tarp žmogaus ir bokšto papėdės = d
Mes turime,
tan θ = priešinga pusė/gretima pusė
įdegis 60° = 100/d
√3 = 100 per dieną [nuo tada 60° = √3]
d = 100/√3
Todėl atstumas tarp žmogaus ir bokšto papėdės yra 100/√3
6 pavyzdys: Raskite tan θ reikšmę, jei sin θ = 7/25 ir sec θ = 25/24.
Sprendimas:
Atsižvelgiant į
sin θ = 7/25
sek θ = 25/24
Mes tai žinome,
sek θ = 1/cos θ
25/24 = 1/cos θ cos θ = 24/25
Mes turime,
tan θ = sin θ/cos θ
= (7/25)/(24/25)
= 7/24
Vadinasi, įdegio θ = 7/24
7 pavyzdys: Raskite tan θ reikšmę, jei cosec θ = 5/3, o θ yra pirmasis kvadranto kampas.
Sprendimas:
Duota, cosec θ = 5/3
Iš pitagoriečių tapatybių mes turime,
123 filmascosec2θ – vaikiška lovelė2θ = 1
vaikiška lovelė2θ = kosek2aš - 1
vaikiška lovelė θ = (5/3)2– 1 = (25/9) – 1 = 16/9
vaikiška lovelė θ = ±√16/9 = ± 4/3
Kadangi θ yra pirmasis kvadranto kampas, tiek kotangentinės, tiek tangentinės funkcijos yra teigiamos.
vaikiška lovelė θ = 4/3
Mes tai žinome,
vaikiška lovelė θ = 1/tan θ
4/3 = 1/tanθ
įdegio θ = 3/4
Vadinasi, įdegio θ = 3/4
8 pavyzdys: Raskite tan 3θ, jei sin θ = 3/7 ir θ yra pirmasis kvadranto kampas.
Sprendimas:
Duota, nuodėmė θ = 12/13
Iš mūsų turimų pitagoriečių tapatybių,
be2θ + cos2θ = 1
cos2θ = 1 – nuodėmė2θ = 1 – (12/13)2
cos2 θ = 1 – (144/169) = 25/169
cos θ = ±√25/169 = ±5/13
Kadangi θ yra pirmasis kvadranto kampas, cos θ yra teigiamas.
cos θ = 5/13
Mes tai žinome,
tan θ = sin θ/cos θ
= (12/25)/(5/13) = 12/5
Vadinasi, tan θ = 12/5
Dabar mes žinome, kad
tan 3θ = (3 tan θ – tan3θ) / (1–3 tan2θ)
įdegis 3θ = 3 × (12/5)

