Galima išmatuoti tris bet kurio matomo ar paliesti objekto matmenis: ilgį, plotį ir aukštį. Yra tam tikrų mūsų namų, kuriuose gyvename, matmenys. Stačiakampio ekrano / monitoriaus, į kurį žiūrite, plotis ir plotis yra viso ilgio. Kiekvienai trimatei geometrinei struktūrai matuojamas paviršiaus plotas ir tūris.
Aera, padengta objekto paviršiumi, yra bet kurio objekto paviršiaus plotas. Tuo tarpu objekte turimos vietos kiekis yra tūris.
Turinys
- Paviršiaus plotas
- Bendras paviršiaus plotas
- Išlenkto paviršiaus plotas / šoninis paviršiaus plotas
- Apimtis
- Paviršiaus plotų ir tūrių pavyzdžiai
- DUK apie paviršiaus ploto ir tūrio formules
Paviršiaus plotas
Paviršiaus plotą ir tūrį galima apskaičiuoti bet kokiai trimačiai (3D) geometrinei formai. Bet kurios srities paviršius yra sritis, kurią užima objekto paviršius. Tūris yra objekte turimos vietos kiekis. Turime įvairių formų, tokių kaip pusrutulis, rutulys, kubas, stačiakampis, cilindras ir kt. Visos trimatės formos turi plotą ir tūrį. Tačiau dvimatės formos, tokios kaip kvadratai, stačiakampiai, trikampiai, apskritimai ir kt.
Čia dvimačiai, galime išmatuoti tik plotą. Plotas, kurį trimačio objekto užima išorinis paviršius, vadinamas paviršiaus plotu. Jis matuojamas kvadratiniais vienetais.
Teritorija yra dviejų tipų:
- Bendras paviršiaus plotas
- Išlenkto paviršiaus plotas / šoninis paviršiaus plotas
Bendras paviršiaus plotas
Plotas, įskaitant pagrindą (-ius) ir išlenktą dalį, atitinka bendrą paviršiaus plotą. Tai ploto, kurį uždaro objekto paviršius, dydis. Jei forma turi išlenktą pagrindą ir paviršių, tai dviejų sričių suma būtų bendras plotas. Bendras paviršiaus plotas gali būti apibrėžtas kaip bendras plotas, kurį dengia objektas, įskaitant jo pagrindą ir išlenktą dalį. Jei objektas turi ir pagrindą, ir išlenktą plotą, bendras paviršiaus plotas bus lygus pagrindo ir išlenkto ploto sumai.
- Bendras paviršiaus plotas yra bendras plotas, kurį užima objektas.
- Pavyzdžiui, kaip pavyzdį paimkite stačiakampį stačiakampį, kuriame yra 6 paviršiai, 12 briaunų ir 8 viršūnės.
Bendras paviršiaus plotas = bazinis plotas + išlenktas plotas
python programas
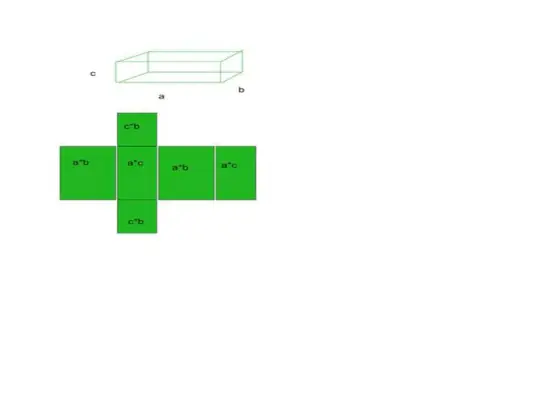
- Visų tų 6 sričių suma bus mūsų bendras konkrečios formos paviršiaus plotas
Pavyzdys:
Žemiau pateikta stačiakampė, kurios matmuo nurodytas kaip ilgis = 8 cm, plotis = 4 cm ir aukštis = 6 cm, raskite stačiakampio TSA
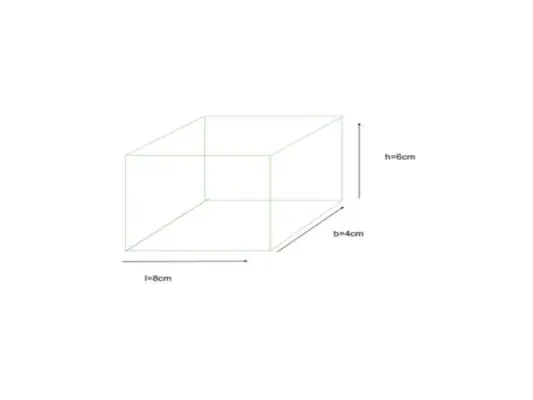
duota l = 8cm, b = 4cm, h = 6cm
TSA = 2 ((l * b) + (l * h) + (b * h))
= 2((8 * 4) + (8 * 6) + (4 * 6))
= 2((32) + (48) + (24))
= 2 (104)
= 208
Kuboido TSA yra 208 cm.
Išlenkto paviršiaus plotas / šoninis paviršiaus plotas
Išlenkto paviršiaus plotas, išskyrus jo centrą, atitinka tik išlenktos formos (-ių) dalies plotą. Tokioms formoms kaip kūgis jis dažnai vadinamas šoniniu paviršiaus plotu. Šoninis paviršiaus plotas gali būti apibrėžtas kaip sritis, apimanti tik išlenktą objekto paviršiaus plotą arba objekto šoninio paviršiaus plotą, neįskaitant objekto pagrindo ploto. Šoninis paviršiaus plotas taip pat žinomas kaip išlenktas paviršiaus plotas.
Dauguma formų ar objektų nurodo išlenkto paviršiaus plotą, o formos arba objekto formos cilindras nurodo jį kaip šoninį paviršiaus plotą. Paprasčiau tariant, mums matoma sritis vadinama šoniniu paviršiaus plotu. Pavyzdžiui, apsvarstykite cilindrą, kaip parodyta toliau pateiktame paveikslėlyje.
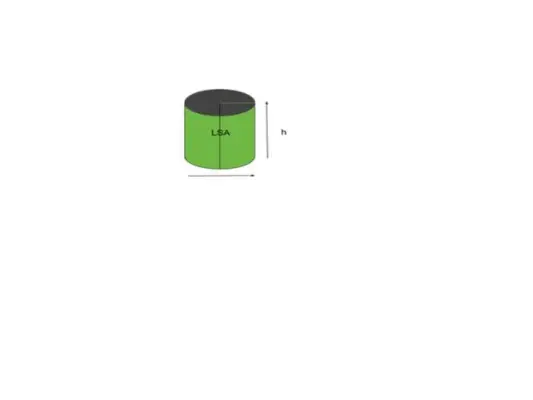
Apimtis
Tūris yra tam tikrame 3D objekte esančios erdvės kiekis. Bendras erdvės kiekis, kurį užima objektas ar medžiaga, vadinamas tūriu. Jis matuojamas kubiniais vienetais.
Paviršiaus ploto ir tūrio formulės
Pateiktoje lentelėje yra bendras paviršiaus plotas, išlenkto paviršiaus plotas / šoninis paviršiaus plotas ir įvairių formų tūris.
| Formos pavadinimas | Išlenktas paviršiaus plotas | Bendras paviršiaus plotas | Apimtis |
|---|---|---|---|
| Kuboidas | 2h (l + b) | 2 (lb + bh + hl) | l * b * h |
| kubas | 4a2 | 6a2 | a3 |
| Cilindras | 2πrh | 2π(r + h) | πr2h |
| Sfera | 4πr2 grupavimas | 4πr2 | 4/3π r3 |
| Kūgis | πrl | πr(r + l) | 1/3π r2h |
| Pusrutulis | 2pr2 | 3πr2 | 2/3π r3 |
Skaityti daugiau:
- Piramidės paviršiaus plotas
- Cilindro paviršiaus plotas
- Pusrutulio paviršiaus plotas
- Sferos paviršiaus plotas
- Kuboido paviršiaus plotas
Paviršiaus plotų ir tūrių pavyzdžiai
1 pavyzdys: 2 kubeliai, kurių kiekvieno tūris yra 512 cm 3 yra sujungti iki galo. Raskite gautos stačiakampės paviršiaus plotą?
Sprendimas:
Atsižvelgiant į
Kiekvieno kubo tūris (V) = 512 cm3
dabar galime teigti, kad a3= 512 cm3
∴ Kubo kraštinė, ty a = 8 cm
Dabar gauto stačiakampio plotis ir ilgis bus po 8 cm, o aukštis - 16 cm.
Taigi, stačiakampio paviršiaus plotas (TSA) = 2 (lb + bh + lh)
Dabar, sudėję vertybes, gauname,
= 2 (8 × 16 + 8 × 8 + 16 × 8) cm 2
= (2 × 320) = 640 cm 2
Vadinasi, stačiakampio TSA = 640 cm 2
2 pavyzdys: Turime 14 cm skersmens ir 2 cm ilgio cilindrinę žvakę. Jis išlydomas, kad susidarytų 7 cm × 11 cm × 1 cm matmenų stačiakampė žvakė. Kiek kuboidinių žvakių galima įsigyti?
Sprendimas:
Cilindrinės žvakės matmenys:
Cilindrinės žvakės spindulys = 14/2 cm = 7 cm
Aukštis/storis = 2 cm
Vienos cilindrinės žvakės tūris = πr2h = π x 7 x 7 x (2) cm3= 308 cm3.
Statutinės formos tūris žvakė = 7 x 11 x 1 = 77 cm3
Vadinasi, kuboidinių žvakių skaičius = stačiakampės žvakės tūris / vienos cilindrinės žvakės tūris = 308/77 = 4
Taigi galime gauti 4 kubo formos žvakes.
3 pavyzdys: Moteris nori iš molio pastatyti sferinį žaislinį rutulį, kurio spindulys būtų lygus jos nešiojamos apyrankės spinduliui. Atsižvelgdama į tai, kad apyrankė yra apskritimo formos, ji taip pat nori, kad apyrankės plotas būtų lygus sferos tūriui. Išsiaiškinkite jos nešiojamos apyrankės spindulį?
Sprendimas:
Tegul r yra apyrankės spindulys ir sfera,
Mums buvo duota, kad sferos tūris yra lygus apyrankės plotui:
Vadinasi,
πr2= 4/3 πr3
⇒ r = 3/4
Taigi apyrankės spindulys yra 3/4 vienetų.
4 pavyzdys: Nustatyta, kad dešiniojo apskrito kūgio nuožulnus aukštis yra 25 cm, o aukštis - 24 cm. Rasti išlenktą kūgio paviršiaus plotą?
Sprendimas:
Kūgio išlenkto paviršiaus ploto formulė yra πrl. Kur r yra kūgio spindulys, o l yra kūgio nuožulnus aukštis.
Čia kūgis yra dešinysis apskritas kūgis.
rekha amžiusTaigi kūgio spindulys būtų toks:
r = sqrt{l^2 – h^2}
=>r = sqrt{25^2 – 24^2}
=> r = 7 cm.
Dabar apskaičiuojant išlenktą paviršių:
Reikalingas plotas = (22/7) * 7 * 25 = 550 cm2
Taigi kūgio išlenkto paviršiaus plotas yra 550 cm 2 .
5 pavyzdys: Raskite cilindro, kurio pagrindo spindulys 6 coliai ir 14 colių aukštis, šoninio paviršiaus plotą.
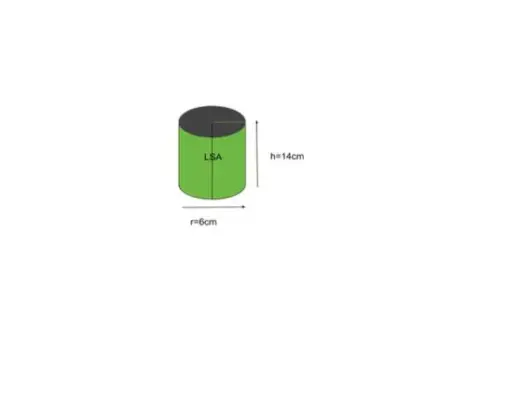
Sprendimas:
Duotas spindulys r = 6, aukštis h = 14
LSA = 2∏rh
= 2 * ∏ * 6 * 14
= 168∏
= 527 787
= 528.
Nurodyto cilindro LSA yra 528 cm .
Praktinis klausimas dėl paviršiaus plotų ir tūrių
Įvairūs Praktiniai klausimai apie paviršiaus plotus ir tūrį formulės yra:
Q1. Raskite kubo, kurio kraštinės ilgis yra 5 centimetrai, paviršiaus plotą.
Q2. Apskaičiuokite 3 metrų spindulio rutulio tūrį.
Q3. Nustatykite cilindro, kurio spindulys yra 4 centimetrai ir aukštis 8 centimetrai, bendrą paviršiaus plotą.
4 klausimas. Raskite kūgio, kurio spindulys yra 6 coliai ir aukštis 10 colių, tūrį.
Q5. Apskaičiuokite stačiakampės prizmės, kurios ilgis 7 metrai, plotis 4 metrai ir aukštis 6 metrai, paviršiaus plotą.
DUK apie paviršiaus ploto ir tūrio formules
Kokios yra paviršiaus ploto ir tūrio formulės?
Aukščiau esančiame straipsnyje pridėtos įvairios paviršiaus ploto ir tūrio formulės.
Kokia yra 10 klasės paviršiaus ploto tūrio formulė?
10 paviršiaus ploto ir tūrio klasės formulę sudaro:
| Formos pavadinimas | Išlenktas paviršiaus plotas | Bendras paviršiaus plotas | Apimtis |
|---|---|---|---|
| Kuboidas java perdavė char į eilutę | 2h (l + b) | 2 (lb + bh + hl) | l × b × h |
| kubas | 4a2 | 6a2 | a3 |
| Cilindras | 2πrh | 2π(r + h) | πr2h |
| Sfera | 4πr2 | 4πr2 | 4/3π r3 |
| Kūgis | πrl | πr(r + l) | 1/3π r2h |
| Pusrutulis | 2pr2 | 3πr2 | 2/3π r3 |
Kokia yra kuboido paviršiaus ploto ir tūrio formulė?
- Kuboido paviršiaus plotas = 2 (lb + bh + hl)
- Kubiodo tūris = l × b × h
Kas yra paviršiaus plotas ir tūris?
Paviršiaus plotas yra visų kietojo kūno paviršių plotas, o jo tūris yra plotas, kurį užima dugnas.
