Realiame pasaulyje ne visi duomenys, su kuriais dirbame, turi tikslinį kintamąjį. Tokio tipo duomenų negalima analizuoti naudojant prižiūrimus mokymosi algoritmus. Mums reikia neprižiūrimų algoritmų pagalbos. Vienas iš populiariausių nekontroliuojamo mokymosi analizės tipų yra klientų segmentavimas tiksliniams skelbimams arba medicininiam vaizdavimui, siekiant rasti nežinomas ar naujas užkrėstas sritis ir daug kitų naudojimo atvejų, kuriuos toliau aptarsime šiame straipsnyje.
Turinys
- Kas yra klasterizavimas?
- Klasterizacijos tipai
- Klasterizacijos panaudojimas
- Klasterizacijos algoritmų tipai
- Klasterizacijos pritaikymas įvairiose srityse:
- Dažnai užduodami klausimai (DUK) apie grupavimą
Kas yra klasterizavimas?
Duomenų taškų grupavimo, atsižvelgiant į jų panašumą, užduotis vadinama grupavimu arba klasterių analize. Šis metodas yra apibrėžtas skyriuje Mokymasis be priežiūros , kuriuo siekiama gauti įžvalgų iš nepažymėtų duomenų taškų, ty kitaip nei prižiūrimas mokymasis mes neturime tikslinio kintamojo.
Klasterizacijos tikslas - sudaryti vienarūšių duomenų taškų grupes iš nevienalyčio duomenų rinkinio. Jis įvertina panašumą pagal metriką, pvz., Euklido atstumą, kosinuso panašumą, Manheteno atstumą ir kt., tada sugrupuoja taškus, kurių panašumo balas didžiausias.
Pavyzdžiui, toliau pateiktame grafike aiškiai matome, kad pagal atstumą susidaro 3 apskriti klasteriai.
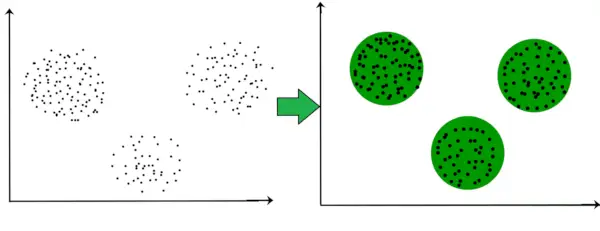
Dabar nebūtina, kad suformuotos sankaupos būtų apskritos. Klasterių forma gali būti savavališka. Yra daug algoritmų, kurie gerai veikia aptikdami savavališkos formos grupes.
skaitymas iš csv failo java
Pavyzdžiui, žemiau pateiktame grafike matome, kad suformuoti klasteriai nėra apskritimo formos.

Klasterizacijos tipai
Apskritai, yra 2 tipų grupavimas, kurį galima atlikti norint sugrupuoti panašius duomenų taškus:
- Sunkus klasterizavimas: Šio tipo klasterizuojant kiekvienas duomenų taškas visiškai priklauso klasteriui arba ne. Pavyzdžiui, tarkime, kad yra 4 duomenų taškai ir turime juos sugrupuoti į 2 grupes. Taigi kiekvienas duomenų taškas priklausys 1 arba 2 klasteriui.
| Duomenų taškai | Klasteriai |
|---|---|
| A | C1 |
| B | C2 |
| C | C2 |
| D | C1 |
- Minkštas grupavimas: Taikant tokio tipo klasterizavimą, užuot priskyręs kiekvieną duomenų tašką į atskirą klasterį, įvertinama tikimybė arba tikimybė, kad tas taškas bus tas klasteris. Pavyzdžiui, tarkime, kad yra 4 duomenų taškai ir turime juos sugrupuoti į 2 grupes. Taigi mes įvertinsime duomenų taško, priklausančio abiem klasteriams, tikimybę. Ši tikimybė apskaičiuojama visiems duomenų taškams.
| Duomenų taškai | C1 tikimybė | C2 tikimybė |
| A | 0,91 | 0.09 |
| B | 0.3 | 0.7 |
| C | 0.17 | 0,83 |
| D | 1 | 0 |
Klasterizacijos panaudojimas
Dabar, prieš pradėdami nuo grupavimo algoritmų tipų, apžvelgsime grupavimo algoritmų naudojimo atvejus. Klasterizacijos algoritmai dažniausiai naudojami:
- Rinkos segmentacija – Įmonės naudoja klasterizavimą savo klientams grupuoti ir naudoja tikslines reklamas, kad pritrauktų daugiau auditorijos.
- Socialinių tinklų analizė – Socialinės žiniasklaidos svetainės naudoja jūsų duomenis, kad suprastų jūsų naršymo elgseną ir pateiktų tikslines draugų ar turinio rekomendacijas.
- Medicininis vaizdavimas – gydytojai naudoja klasterizavimą, kad nustatytų ligotas sritis diagnostiniuose vaizduose, pvz., rentgeno spinduliuose.
- Anomalijų aptikimas – Norėdami rasti išimčių realaus laiko duomenų rinkinio sraute arba prognozuoti nesąžiningus sandorius, galime juos identifikuoti naudodami grupes.
- Supaprastinkite darbą su dideliais duomenų rinkiniais – užbaigus grupavimą kiekvienam klasteriui suteikiamas klasterio ID. Dabar galite sumažinti visą funkcijų rinkinio funkcijų rinkinį į klasterio ID. Klasterizavimas yra efektyvus, kai jis gali būti sudėtingas atvejis su paprastu klasterio ID. Naudojant tą patį principą, duomenų grupavimas gali supaprastinti sudėtingus duomenų rinkinius.
Yra daug daugiau grupių naudojimo atvejų, tačiau yra keletas pagrindinių ir įprastų grupavimo atvejų. Toliau aptarsime grupavimo algoritmus, kurie padės atlikti aukščiau nurodytas užduotis.
Klasterizacijos algoritmų tipai
Paviršiaus lygmeniu grupavimas padeda analizuoti nestruktūrizuotus duomenis. Grafikas, trumpiausias atstumas ir duomenų taškų tankis yra keletas elementų, turinčių įtakos klasterio formavimuisi. Klasterizavimas yra procesas, kurio metu nustatoma, kiek objektai yra susiję, remiantis metrika, vadinama panašumo matu. Panašumo metriką lengviau rasti mažesniuose funkcijų rinkiniuose. Padidėjus funkcijų skaičiui, tampa sunkiau sukurti panašumo priemones. Priklausomai nuo duomenų gavyboje naudojamo klasterizacijos algoritmo tipo, duomenims iš duomenų rinkinių grupuoti naudojami keli metodai. Šioje dalyje aprašomi klasterizacijos metodai. Įvairių tipų klasterizacijos algoritmai yra:
- Centroidinis klasterizavimas (skirstymo metodai)
- Tankiu pagrįstas grupavimas (modeliu pagrįsti metodai)
- Ryšiais pagrįstas grupavimas (hierarchinis grupavimas)
- Paskirstymu pagrįstas grupavimas
Trumpai apžvelgsime kiekvieną iš šių tipų.
1. Padalijimo metodai yra patys paprasčiausi klasterizacijos algoritmai. Jie grupuoja duomenų taškus pagal jų artumą. Paprastai šiems algoritmams pasirinktas panašumo matas yra Euklido atstumas, Manheteno atstumas arba Minkovskio atstumas. Duomenų rinkiniai yra suskirstyti į iš anksto nustatytą skaičių grupių, o kiekviena grupė nurodoma reikšmių vektoriumi. Palyginus su vektoriaus reikšme, įvesties duomenų kintamasis nesiskiria ir prisijungia prie klasterio.
pėdos prieš pėdą
Pagrindinis šių algoritmų trūkumas yra reikalavimas, kad intuityviai arba moksliškai (naudodami alkūnės metodą) nustatytume klasterių skaičių k, prieš bet kuriai klasterizavimo mašininio mokymosi sistemai pradedant skirstyti duomenų taškus. Nepaisant to, tai vis dar yra populiariausias klasterizacijos tipas. K reiškia ir K-medoidai grupavimas yra keletas tokio tipo klasterizacijos pavyzdžių.
2. Tankiu pagrįstas grupavimas (modeliu pagrįsti metodai)
Tankiu pagrįstas klasterizavimas, modeliu pagrįstas metodas, randa grupes pagal duomenų taškų tankį. Priešingai nei centroidais pagrįstas klasterizavimas, kuris reikalauja, kad klasterių skaičius būtų iš anksto nustatytas ir būtų jautrus inicijavimui, tankumu pagrįstas grupavimas automatiškai nustato grupių skaičių ir yra mažiau jautrus pradinėms pozicijoms. Jie puikiai tvarko skirtingų dydžių ir formų grupes, todėl puikiai tinka duomenų rinkiniams su netaisyklingos formos arba persidengiančiais klasteriais. Šie metodai valdo tiek tankius, tiek negausius duomenų regionus, sutelkdami dėmesį į vietinį tankį ir gali atskirti įvairių morfologijų grupes.
Priešingai, grupavimas centroidais, kaip ir k vidurkis, turi problemų ieškant savavališkos formos klasterių. Dėl iš anksto nustatyto klasterio reikalavimų skaičiaus ir didelio jautrumo pradinei centroidų pozicijai rezultatai gali skirtis. Be to, centroidais pagrįstų metodų tendencija kurti sferines arba išgaubtas grupes riboja jų gebėjimą valdyti sudėtingas ar netaisyklingos formos grupes. Apibendrinant galima pasakyti, kad tankiu pagrįstas grupavimas pašalina centroidų metodų trūkumus, nes savarankiškai pasirenka klasterių dydžius, yra atsparus inicijavimui ir sėkmingai fiksuoja įvairaus dydžio ir formos grupes. Populiariausias tankiu pagrįstas klasterizacijos algoritmas yra DBSCAN .
3. Ryšiais pagrįstas grupavimas (hierarchinis grupavimas)
Susijusių duomenų taškų surinkimo į hierarchines grupes metodas vadinamas hierarchiniu klasterizavimu. Į kiekvieną duomenų tašką iš pradžių atsižvelgiama kaip į atskirą klasterį, kuris vėliau sujungiamas su panašiausiomis grupėmis, kad būtų sudarytas vienas didelis klasteris, kuriame yra visi duomenų taškai.
Pagalvokite, kaip galite sutvarkyti daiktų kolekciją pagal jų panašumą. Kiekvienas objektas prasideda kaip atskiras klasteris medžio apačioje, kai naudojamas hierarchinis klasterizavimas, kuris sukuria dendrogramą, į medį panašią struktūrą. Tada artimiausios klasterių poros sujungiamos į didesnes grupes, algoritmui išnagrinėjus, kiek objektai yra panašūs vienas į kitą. Kai kiekvienas objektas yra viename klasteryje medžio viršuje, sujungimo procesas baigtas. Įvairių detalumo lygių tyrinėjimas yra vienas smagiausių dalykų, susijusių su hierarchiniu klasterizavimu. Norėdami gauti nurodytą grupių skaičių, galite pasirinkti iškirpti dendrograma tam tikrame aukštyje. Kuo panašesni du objektai yra klasteryje, tuo arčiau jie yra. Tai galima palyginti su daiktų klasifikavimu pagal jų šeimos medžius, kai artimiausi giminaičiai yra susitelkę, o platesnės šakos reiškia bendresnius ryšius. Yra du hierarchinio klasterizavimo būdai:
- Skiriamasis klasterizavimas : Taikant metodą „iš viršaus į apačią“, visi duomenų taškai yra vienos didelės klasterio dalis, o tada šis klasteris suskirstomas į mažesnes grupes.
- Aglomeracinis klasterizavimas : Taikant metodą „iš apačios į viršų“, visi duomenų taškai laikomi atskirų klasterių dalimi, o tada šie klasteriai sujungiami į vieną didelę klasterį su visais duomenų taškais.
4. Paskirstymu pagrįstas klasterizavimas
Naudojant pasiskirstymu pagrįstą grupavimą, duomenų taškai generuojami ir suskirstomi pagal jų polinkį patekti į tą patį tikimybių skirstinį (pvz., Gauso, dvejetainį ar kitą) duomenų viduje. Duomenų elementai grupuojami naudojant tikimybe pagrįstą skirstinį, pagrįstą statistiniais skirstiniais. Įtraukiami duomenų objektai, kurie turi didesnę tikimybę būti klasteryje. Mažesnė tikimybė, kad duomenų taškas bus įtrauktas į klasterį, kuo toliau nuo klasterio centrinio taško, kuris yra kiekviename klasteryje.
Reikšmingas tankumu ir ribomis pagrįstų metodų trūkumas yra poreikis a priori nurodyti kai kurių algoritmų grupes, o visų pirma – klasterio formos apibrėžimą daugeliui algoritmų. Turi būti pasirinktas bent vienas derinimas arba hiperparametras, ir nors tai padaryti turėtų būti paprasta, jo suklydimas gali turėti nenumatytų pasekmių. Paskirstymu pagrįstas grupavimas turi neabejotiną pranašumą prieš artumo ir centroidų klasterizacijos metodus lankstumo, tikslumo ir grupių struktūros požiūriu. Esminis klausimas yra tas, kad norint išvengti perdėtas , daugelis grupavimo metodų veikia tik su imituotais arba pagamintais duomenimis arba kai didžioji duomenų taškų dalis tikrai priklauso iš anksto nustatytam paskirstymui. Populiariausias paskirstymu pagrįstas grupavimo algoritmas yra Gauso mišinio modelis .
Klasterizacijos pritaikymas įvairiose srityse:
- Rinkodara: Jis gali būti naudojamas apibūdinti ir atrasti klientų segmentus rinkodaros tikslais.
- Biologija: Jis gali būti naudojamas klasifikuojant įvairias augalų ir gyvūnų rūšis.
- Bibliotekos: Jis naudojamas grupuojant įvairias knygas pagal temas ir informaciją.
- Draudimas: Jis naudojamas siekiant pripažinti klientus, jų politiką ir nustatyti sukčiavimą.
- Miesto planavimas: Jis naudojamas namų grupėms sudaryti ir jų vertėms tirti pagal jų geografinę padėtį ir kitus esamus veiksnius.
- Žemės drebėjimo tyrimai: Sužinoję apie žemės drebėjimo paveiktas zonas galime nustatyti pavojingas zonas.
- Vaizdo apdorojimas : grupavimas gali būti naudojamas panašiems vaizdams grupuoti, vaizdams klasifikuoti pagal turinį ir vaizdų duomenų šablonams nustatyti.
- Genetika: Klasterizavimas naudojamas genams, turintiems panašius ekspresijos modelius, grupuoti ir genų tinklams, kurie kartu veikia biologiniuose procesuose, nustatyti.
- Finansai: Klasterizavimas naudojamas rinkos segmentams pagal klientų elgseną nustatyti, akcijų rinkos duomenų modeliams nustatyti ir investicinių portfelių rizikai analizuoti.
- Klientų aptarnavimas: Klasterizavimas naudojamas klientų užklausoms ir skundams suskirstyti į kategorijas, nustatyti bendrąsias problemas ir kurti tikslinius sprendimus.
- Gamyba : Klasterizavimas naudojamas panašiems produktams grupuoti, gamybos procesams optimizuoti ir gamybos procesų defektams nustatyti.
- Medicininė diagnozė: Klasterizavimas naudojamas pacientams, turintiems panašių simptomų ar ligų, grupuoti, o tai padeda nustatyti tikslią diagnozę ir nustatyti veiksmingus gydymo būdus.
- Sukčiavimo aptikimas: Klasterizavimas naudojamas siekiant nustatyti įtartinus finansinių operacijų modelius ar anomalijas, kurios gali padėti aptikti sukčiavimą ar kitus finansinius nusikaltimus.
- Eismo analizė: Klasterizavimas naudojamas panašiems eismo duomenų modeliams, pvz., piko valandoms, maršrutams ir greičiams, grupuoti, o tai gali padėti pagerinti transporto planavimą ir infrastruktūrą.
- Socialinių tinklų analizė: Klasterizavimas naudojamas bendruomenėms ar grupėms socialiniuose tinkluose nustatyti, o tai gali padėti suprasti socialinį elgesį, įtaką ir tendencijas.
- Kibernetinė sauga: Klasterizavimas naudojamas panašiems tinklo srauto ar sistemos elgsenos modeliams grupuoti, o tai gali padėti aptikti kibernetines atakas ir jų išvengti.
- Klimato analizė: Klasterizavimas naudojamas panašiems klimato duomenų modeliams, tokiems kaip temperatūra, krituliai ir vėjas, grupuoti, o tai gali padėti suprasti klimato kaitą ir jos poveikį aplinkai.
- Sporto analizė: Klasterizavimas naudojamas panašiems žaidėjų ar komandos veiklos duomenų modeliams grupuoti, o tai gali padėti analizuoti žaidėjo ar komandos stipriąsias ir silpnąsias puses bei priimti strateginius sprendimus.
- Nusikaltimų analizė: Klasterizavimas naudojamas panašiems nusikaltimų duomenų modeliams, pvz., vietai, laikui ir tipui, grupuoti, o tai gali padėti nustatyti nusikalstamumo židinius, numatyti būsimas nusikalstamumo tendencijas ir tobulinti nusikalstamumo prevencijos strategijas.
Išvada
Šiame straipsnyje aptarėme grupavimą, jo tipus ir programas realiame pasaulyje. Neprižiūrimas mokymasis apima daug daugiau, o klasterio analizė yra tik pirmas žingsnis. Šis straipsnis gali padėti pradėti naudoti grupavimo algoritmus ir sukurti naują projektą, kurį galima įtraukti į savo portfelį.
Dažnai užduodami klausimai (DUK) apie grupavimą
K. Koks yra geriausias klasterizacijos metodas?
10 geriausių klasterizacijos algoritmų yra šie:
- K reiškia klasterizavimą
- Hierarchinis klasterizavimas
- DBSCAN (tankiu pagrįstas erdvinis programų su triukšmu grupavimas)
- Gauso mišinio modeliai (GMM)
- Aglomeracinis klasterizavimas
- Spektrinis klasterizavimas
- Vidutinio poslinkio grupavimas
- Afiniteto plitimas
- OPTIKA (taškų užsakymas identifikuoti grupavimo struktūrą)
- Beržas (subalansuotas iteracinis redukavimas ir grupavimas naudojant hierarchijas)
K. Kuo skiriasi grupavimas ir klasifikavimas?
Pagrindinis skirtumas tarp grupavimo ir klasifikavimo yra tas, kad klasifikavimas yra prižiūrimas mokymosi algoritmas, o grupavimas yra neprižiūrimas mokymosi algoritmas. Tai yra, mes taikome grupavimą tiems duomenų rinkiniams, kuriuose nėra tikslinio kintamojo.
K. Kokie yra klasterizacijos analizės pranašumai?
Duomenys gali būti suskirstyti į reikšmingas grupes, naudojant stiprią analitinę klasterių analizės įrankį. Galite naudoti jį norėdami tiksliai nustatyti segmentus, rasti paslėptus modelius ir pagerinti sprendimus.
K. Kuris yra greičiausias klasterizacijos metodas?
K-means klasterizavimas dažnai laikomas greičiausiu klasterizacijos metodu dėl savo paprastumo ir skaičiavimo efektyvumo. Ji kartotiškai priskiria duomenų taškus artimiausiam klasterio centroidui, todėl tinka dideliems duomenų rinkiniams, kurių matmenys yra maži, ir nedidelis grupių skaičius.
pagrindinis raktas ir sudėtinis raktas sql
K. Kokie yra grupavimo apribojimai?
Klasterizacijos apribojimai apima jautrumą pradinėms sąlygoms, priklausomybę nuo parametrų pasirinkimo, sunkumus nustatant optimalų grupių skaičių ir iššūkius, susijusius su didelių matmenų ar triukšmingų duomenų apdorojimu.
K. Nuo ko priklauso klasterizacijos rezultato kokybė?
Klasterizacijos rezultatų kokybė priklauso nuo tokių veiksnių kaip algoritmo pasirinkimas, atstumo metrika, klasterių skaičius, inicijavimo metodas, išankstinio duomenų apdorojimo metodai, klasterių vertinimo metrika ir srities žinios. Šie elementai bendrai įtakoja klasterizacijos rezultato efektyvumą ir tikslumą.
