logo

TechCodeview

Stipriai sujungti komponentai

Stipriai sujungti komponentai (SCC) yra pagrindinė grafų teorijos ir algoritmų sąvoka. Nukreiptame grafike a Tvirtai sujungtas komponentas yra viršūnių poaibis, kuriame kiekviena poaibio viršūnė pasiekiama iš visų kitų to paties poaibio viršūnių, kertant nukreiptas briaunas. Suradę SCC grafiko naudojimas gali suteikti svarbių įžvalgų apie grafiko struktūrą ir ryšį, naudojant įvairiose srityse, pvz. socialinių tinklų analizė, žiniatinklio tikrinimas ir tinklo maršruto parinkimas . Šioje pamokoje bus nagrinėjamas apibrėžimas, savybės ir veiksmingi algoritmai, skirti atpažinti stipriai susietus komponentus grafinių duomenų struktūrose.

tinklo topologija

Turinys



Kas yra stipriai sujungti komponentai (SCC)?

A stipriai sujungtas komponentas nukreipto grafo yra maksimalus pografas, kuriame kiekviena viršūnių pora yra abipusiai pasiekiama. Tai reiškia, kad bet kuriuose dviejuose šio pografo mazguose A ir B yra kelias nuo A iki B ir kelias iš B į A.

Pavyzdžiui: Žemiau pateiktame grafike yra du stipriai sujungti komponentai {1,2,3,4} ir {5,6,7}, nes yra kelias nuo kiekvienos viršūnės iki kiekvienos kitos to paties stipriai sujungto komponento viršūnės.

scc_fianldrawio

Tvirtai sujungtas komponentas



Kodėl stipriai sujungti komponentai (SCC) yra svarbūs?

SCC supratimas yra labai svarbus įvairioms programoms, tokioms kaip:

  • Tinklo analizė : Identifikuoja glaudžiai tarpusavyje sujungtų mazgų grupes.
  • Žiniatinklio tikrintuvų optimizavimas : glaudžiai susietų žiniatinklio grafiko dalių nustatymas.
  • Priklausomybės sprendimas : programinėje įrangoje suprasti, kurie moduliai yra tarpusavyje susiję.

Skirtumas tarp sujungtų ir stipriai sujungtų komponentų ( SCC)

Ryšys a neorientuotas grafikas nurodo, ar dvi viršūnės pasiekiamos viena nuo kitos, ar ne. Sakoma, kad dvi viršūnės yra sujungtos, jei tarp jų yra kelias. Tuo tarpu Stipriai sujungtas taikomas tik nukreipti grafikai . Nukreipto grafo pografas laikomas an Stipriai sujungti komponentai (SCC) tada ir tik tada, kai kiekvienai viršūnių porai A ir B , yra kelias iš A į B ir kelias iš B į A . Pažiūrėkime, kodėl standartinis dfs metodas susietiems komponentams rasti grafike negali būti naudojamas stipriai sujungtiems komponentams nustatyti.

Apsvarstykite šią diagramą:



scc_fianldrawio

Dabar pradėkime a dfs skambinkite iš 1 viršūnės, kad aplankytumėte kitas viršūnes.

dfs_finaldrawio

Kodėl įprastu DFS metodu negalima rasti stipriai sujungtų komponentų?

Visas viršūnes galima pasiekti iš 1 viršūnės. Tačiau 1 ir 5, 6, 7 viršūnės negali būti tame pačiame stipriai sujungtame komponente, nes nėra nukreipto kelio iš viršūnės 5, 6 arba 7 į viršūnę 1. Grafas turi dvi stipriai sujungtas dalis. sujungti komponentai {1,2,3,4} ir {5,6,7}. Taigi įprasto dfs metodo negalima naudoti norint rasti stipriai sujungtus komponentus.

kas yra ymail

Dviejų tvirtai sujungtų komponentų sujungimas vienakrypčiu kraštu

Du skirtingi sujungti komponentai tampa vienu komponentu, jei tarp vieno komponento viršūnės ir kito komponento viršūnės pridedama briauna. Tačiau taip nėra stipriai sujungtų komponentų atveju. Du stipriai sujungti komponentai netampa vienu stipriai sujungtu komponentu, jei yra tik vienakryptis kraštas nuo vieno SCC iki kito SCC.

Java dinaminis masyvas

unidrawio-(2)

Brutalios jėgos metodas ieškant stipriai susijusių komponentų

Paprastas metodas bus kiekvienai viršūnei i (kuri nėra jokio stipriai komponento dalis) rasti viršūnes, kurios bus stipriai sujungto komponento, kuriame yra viršūnė i, dalis. Dvi viršūnės i ir j bus tame pačiame stipriai sujungtame komponente, jei yra nukreiptas kelias iš viršūnės i į viršūnę j ir atvirkščiai.

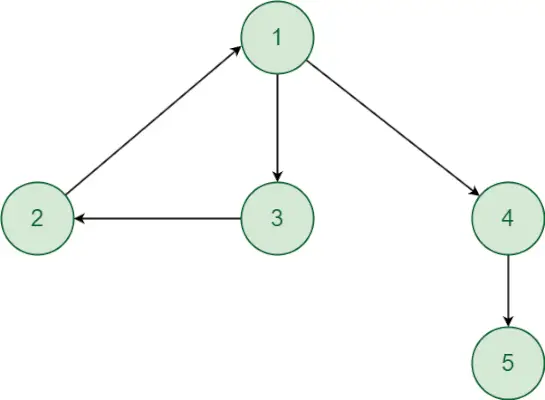
Supraskime metodą naudodami šį pavyzdį:

piešimo pavyzdys

  • Pradedant nuo 1 viršūnės. Yra kelias nuo 1 viršūnės iki 2 viršūnės ir atvirkščiai. Panašiai yra kelias nuo 1 viršūnės iki 3 viršūnės ir atvirkščiai. Taigi, 2 ir 3 viršūnės bus tame pačiame stipriai sujungtame komponente kaip ir 1 viršūnė. Nors yra nukreiptas kelias iš 1 viršūnės į viršūnę 4 ir viršūnę 5. Tačiau nėra nukreipto kelio iš viršūnės 4,5 į viršūnę 1, taigi viršūnė 4 ir 5 nebus tame pačiame stipriai sujungtame komponente kaip 1 viršūnė. Taigi 1, 2 ir 3 viršūnės sudaro stipriai susietą komponentą.
  • 2 ir 3 viršūnėse jau nustatytas stipriai sujungtas komponentas.
  • 4 viršūnėje yra kelias nuo 4 viršūnės iki 5 viršūnės, bet nėra kelio nuo 5 viršūnės iki 4 viršūnės. Taigi 4 ir 5 viršūnės nebus tame pačiame stipriai sujungtame komponente. Taigi ir „Vertex 4“, ir „Vertex 5“ bus vieno tvirtai sujungto komponento dalis.
  • Taigi bus 3 tvirtai sujungti komponentai {1,2,3}, {4} ir {5}.

Žemiau pateikiamas aukščiau aprašyto metodo įgyvendinimas:

C++ 
#include  using namespace std; class GFG { public:  // dfs Function to reach destination  bool dfs(int curr, int des, vector>& adj, vektorius & vis) { // Jei curr mazgas yra paskirties, return true if (curr == des) { return true;  } vis[curr] = 1;  for (auto x : adj[curr]) { if (!vis[x]) { if (dfs(x, des, adj, vis)) { return true;  } } } return false;  } // Nurodykite, ar yra kelias nuo šaltinio iki // paskirties bool isPath(int src, int des, vektorius>& adj) { vektorius vis(adj.size() + 1, 0);  return dfs(src, des, adj, vis);  } // Funkcija grąžinti visą stipriai susietą // grafiko komponentą.  vektorius> rastiSCC(int n, vektorius>& a) { // Saugo visus stipriai sujungtus komponentus.  vektorius> ans;  // Išsaugo, ar viršūnė yra bet kurio stipriai // sujungto komponento vektoriaus dalis is_scc(n + 1, 0);  vektorius> adj(n + 1);  už (int i = 0; i< a.size(); i++) {  adj[a[i][0]].push_back(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++) {  if (!is_scc[i]) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // thr part of thidl ist.  vector scc;  scc.push_back(i);  už (int j = i + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa put vertex j  // into the current SCC list.  if (!is_scc[j] && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc[j] = 1;  scc.push_back(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.push_back(scc);  }  }  return ans;  } }; // Driver Code Starts int main() {  GFG obj;  int V = 5;  vector> briaunos{ { 1, 3 }, { 1, 4 }, { 2, 1 }, { 3, 2 }, { 4, 5 } };  vektorius> ans = obj.findSCC(V, briaunos);  cout<< 'Strongly Connected Components are:
';  for (auto x : ans) {  for (auto y : x) {  cout << y << ' ';  }  cout << '
';  } }>
Java 
import java.util.ArrayList; import java.util.List; class GFG {  // dfs Function to reach destination  boolean dfs(int curr, int des, List> adj, sąrašas vis) { // Jei curr mazgas yra tikslas return true if (curr == des) { return true;  } vis.set(curr, 1);  for (int x : adj.get(curr)) { if (vis.get(x) == 0) { if (dfs(x, des, adj, vis)) { return true;  } } } return false;  } // Norėdami sužinoti, ar yra kelias nuo šaltinio iki // paskirties loginis isPath(int src, int des, List> adj) { Sąrašas vis = new ArrayList(adj.size() + 1);  už (int i = 0; i<= adj.size(); i++) {  vis.add(0);  }  return dfs(src, des, adj, vis);  }  // Function to return all the strongly connected  // component of a graph.  List> rastiSCC(int n, sąrašas> a) { // Saugo visus stipriai sujungtus komponentus.  Sąrašas> ans = new ArrayList();  // Saugoma, ar viršūnė yra bet kurio stipriai // prijungtų komponentų sąrašo dalis is_scc = naujas ArrayList(n + 1);  už (int i = 0; i<= n; i++) {  is_scc.add(0);  }  List> adj = naujas ArrayList();  už (int i = 0; i<= n; i++) {  adj.add(new ArrayList());  }  for (List kraštas : a) { adj.get(kraštas.get(0)).add(kraštas.get(1));  } // Pereinamos visos viršūnės, skirtos (int i = 1; i<= n; i++) {  if (is_scc.get(i) == 0) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  List scc = naujas ArrayList();  scc.add(i);  už (int j = i + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (is_scc.get(j) == 0 && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc.set(j, 1);  scc.add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.add(scc);  }  }  return ans;  } } public class Main {  public static void main(String[] args) {  GFG obj = new GFG();  int V = 5;  List> briaunos = naujas ArrayList();  edges.add(new ArrayList(List.of(1, 3)));  edges.add(new ArrayList(List.of(1, 4)));  edges.add(new ArrayList(List.of(2, 1)));  edges.add(new ArrayList(List.of(3, 2)));  edges.add(new ArrayList(List.of(4, 5)));  Sąrašas> ans = obj.findSCC(V, briaunos);  System.out.println('Tvirtai sujungti komponentai yra:');  už (sąrašas x : ans) { for (int y : x) { System.out.print(y + ' ');  } System.out.println();  } } } // Šį kodą sukūrė shivamgupta310570>>Python
C# 
using System; using System.Collections.Generic; class GFG {  // dfs Function to reach destination  public bool Dfs(int curr, int des, List> adj, sąrašas vis) { // Jei curr mazgas yra paskirties vieta, return true if (curr == des) { return true;  } vis[curr] = 1;  foreach (var x in adj[curr]) { if (vis[x] == 0) { if (Dfs(x, des, adj, vis)) { return true;  } } } return false;  } // Norėdami sužinoti, ar yra kelias nuo šaltinio iki paskirties vietos public bool IsPath(int src, int des, List> adj) { var rodyti = naujas sąrašas (adj.Skaičius + 1);  už (int i = 0; i< adj.Count + 1; i++)  {  vis.Add(0);  }  return Dfs(src, des, adj, vis);  }  // Function to return all the strongly connected components of a graph  public List> RastiSCC(int n, sąrašas> a) { // Saugo visus stipriai sujungtus komponentus var ans = new List>();  // Saugoma, ar viršūnė yra bet kurio stipriai sujungto komponento dalis var isScc = naujas sąrašas (n + 1);  už (int i = 0; i< n + 1; i++)  {  isScc.Add(0);  }  var adj = new List>(n + 1);  už (int i = 0; i< n + 1; i++)  {  adj.Add(new List ());  } for (int i = 0; i< a.Count; i++)  {  adj[a[i][0]].Add(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++)  {  if (isScc[i] == 0)  {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  var scc = new List ();  scc.Pridėti(i);  už (int j = i + 1; j<= n; j++)  {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (isScc[j] == 0 && IsPath(i, j, adj) && IsPath(j, i, adj))  {  isScc[j] = 1;  scc.Add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.Add(scc);  }  }  return ans;  } } // Driver Code Starts class Program {  static void Main(string[] args)  {  GFG obj = new GFG();  int V = 5;  List> briaunos = naujas sąrašas> { naujas sąrašas { 1, 3 }, naujas sąrašas { 1, 4 }, naujas sąrašas {2, 1}, naujas sąrašas { 3, 2 }, naujas sąrašas {4, 5}};  Sąrašas> ans = obj.RastiSCC(V, briaunos);  Console.WriteLine('Tvirtai sujungti komponentai yra:');  foreach (var x in ans) { foreach (var y in x) { Console.Write(y + ' ');  } Console.WriteLine();  } } } // Šį kodą sukūrė shivamgupta310570>>Javascript
Išvestis 
Strongly Connected Components are: 1 2 3 4 5>

Laiko sudėtingumas: O(n * (n + m)), nes kiekvienai viršūnių porai mes tikriname, ar tarp jų yra kelias.
Pagalbinė erdvė: O(N)

kaip uždaryti kūrėjo režimą

Veiksmingas metodas ieškant stipriai sujungtų komponentų (SCC)

Norėdami rasti SCC grafike, galime naudoti tokius algoritmus kaip Kosaraju algoritmas arba Tarjano algoritmas . Išnagrinėkime šiuos algoritmus žingsnis po žingsnio.

1. Kosaraju algoritmas :

Kosaraju algoritmas susideda iš dviejų pagrindinių etapų:

  1. Pradinėje diagramoje atliekama pirmoji giluminė paieška (DFS). :
    • Pirmiausia atliekame DFS pradiniame grafike ir įrašome mazgų pabaigos laikus (t. y. laiką, kai DFS baigia visiškai ištirti mazgą).
  2. DFS vykdymas perkeltoje diagramoje :
    • Tada pakeičiame visų grafiko briaunų kryptis, kad sukurtume perkeltą grafiką.
    • Tada atliekame perkelto grafiko DFS, atsižvelgdami į mazgus mažėjančia tvarka pagal jų užbaigimo laiką, įrašytą pirmajame etape.
    • Kiekvienas DFS perėjimas šiame etape suteiks mums vieną SCC.

Štai supaprastinta Kosaraju algoritmo versija:

  1. DFS originalioje diagramoje : Įrašykite pabaigos laiką.
  2. Perkelkite grafiką : Apverskite visus kraštus.
  3. DFS perkeltoje diagramoje : apdorokite mazgus mažėjančio užbaigimo laiko tvarka, kad surastumėte SCC.

2. Tarjano algoritmas :

Tarjano algoritmas yra efektyvesnis, nes jis suranda SCC viename DFS leidime, naudodamas krūvą ir papildomą apskaitą:

  1. DFS perkėlimas : DFS metu palaikykite kiekvieno mazgo indeksą ir mažiausią indeksą (žemos nuorodos reikšmę), kurią galima pasiekti iš mazgo.
  2. Stack : Sekite mazgus, esančius šiuo metu rekursijos krūvoje (dalis dabartinio SCC tiriama).
  3. SCC identifikavimas : Kai mazgo žemo ryšio reikšmė lygi jo indeksui, tai reiškia, kad radome SCC. Iškelkite visus mazgus iš krūvos, kol pasieksime dabartinį mazgą.

Štai supaprastintas Tarjano algoritmo kontūras:

  1. Inicijuotiindex>iki 0.
  2. Kiekvienam neaplankytam mazgui atlikite DFS.
    • Nustatykite mazgo indeksą ir žemo ryšio reikšmę.
    • Stumkite mazgą ant kamino.
    • Kiekvienam gretimam mazgui atlikite DFS, jei jame nesilankote, arba atnaujinkite žemo ryšio reikšmę, jei ji yra krūvoje.
    • Jei mazgo žemo ryšio reikšmė lygi jo indeksui, iškelkite mazgus iš krūvos, kad sudarytų SCC.

Išvada

Supratimas ir atradimas stipriai sujungti komponentai nukreiptas grafikas yra būtinas daugeliui kompiuterių mokslo programų. Kosaraju's ir Tarjano algoritmai yra veiksmingi būdai identifikuoti SCC, kurių kiekvienas turi savo požiūrį ir privalumus. Įvaldę šias sąvokas galite geriau analizuoti ir optimizuoti sudėtingų tinklų struktūrą ir elgesį.