Standartinė parabolės forma yra y = ax²+ bx + c kur a, b ir c yra tikrieji skaičiai, o a nėra lygus nuliui. Parabolė apibrėžiama kaip aibė visų plokštumos taškų, kurie yra vienodu atstumu nuo fiksuotos linijos ir fiksuoto taško plokštumoje.

Šiame straipsnyje mes išsamiai suprasime, kas yra parabolė, standartinė parabolės lygtis, susiję pavyzdžiai ir kiti.

Turinys

• Kas yra parabolė?
• Parabolės lygtis
• Bendrosios parabolės lygtys
• Standartinės parabolės lygtys
• Parabolės dalys
• Parabolės lygties pavyzdžiai

Kas yra parabolė?

Parabolė yra kūgio pjūvis, apibrėžiamas kaip visų taškų, vienodu atstumu nuo taško, vadinamo židiniu, ir linijos, vadinamos krypties, rinkinys. Standartinės parabolės lygtys priklauso nuo jos orientacijos (atidarymo krypties) ir padėties.

Parabolės lygtis

Parabolės lygtis gali būti parašyta standartine arba bendra forma ir abi jos pridedamos žemiau:

Bendrosios parabolės lygtys

Bendroji parabolės lygtis yra

y = 4a(x – h) ² + k

(arba)

x = 4a(y – k) ² + h

Kur (h, k) yra parabolės viršūnė.

Standartinės parabolės lygtys

Standartinė parabolės lygtis yra

y = kirvis ² + bx + c

(arba)

x = yra ² + + c

kur a niekada negali būti nulis.

Parabolės dalys

Kai kurie svarbūs parabolės terminai ir dalys yra:

• Fokusas: Fokusas yra fiksuotas parabolės taškas.

• Kryptis: Parabolės kryptis yra tiesė, statmena parabolės ašiai.

• Židinio akordas: Akordas, einantis per parabolės židinį ir perpjaunantis parabolę dviejuose skirtinguose taškuose, vadinamas židinio styga.

• Židinio nuotolis: Židinio nuotolis yra atstumas iki taško (x₁, ir₁) ant parabolės nuo židinio.

• Dešinioji pusė: Latus tiesioji žarna yra židinio styga, kuri eina per parabolės židinį ir yra statmena parabolės ašiai. Latus tiesiosios žarnos ilgis yra LL’ = 4a.

• Ekscentriškumas: Taško atstumo nuo židinio ir atstumo nuo krypties santykis vadinamas ekscentriškumu (e). Parabolės ekscentriškumas yra lygus 1, ty e = 1.

Parabolė turi keturias standartines lygtis, pagrįstas parabolės ir jos ašies orientacija. Kiekviena parabolė turi skirtingą skersinę ir konjuguotą ašį.

Parabolės lygtis	Parabolė	Parabolės parametrų formulės
ir 2 = 4ax	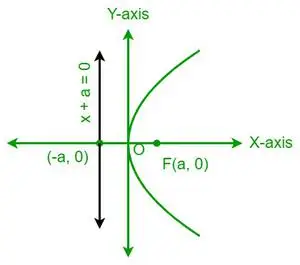Horizontali parabolė	Viršūnė = (0,0) Fokusas = (a, 0) Parabolė atsidaro į dešinę pusę. Ašies lygtis yra y = 0 Krypties lygtis yra x + a = 0 Latus tiesiosios žarnos ilgis = 4a
ir 2 = -4ax	Horizontali parabolė	Viršūnė = (0,0) Fokusuoti = (-a, 0) Parabolė atsidaro į kairę pusę. Ašies lygtis yra y = 0 Krypties lygtis yra x – a = 0 Latus tiesiosios žarnos ilgis = 4a
x 2 = 4ay	Vertikali parabolė	Viršūnė = (0,0) Fokusas = (0, a) Parabolė atsiveria į viršų. Ašies lygtis yra x = 0 Krypties lygtis yra y + a = 0 Latus tiesiosios žarnos ilgis = 4a
x 2 = -4ay	Vertikali parabolė	Viršūnė = (0,0) Fokusuoti = (0, -a) Parabolė atsidaro žemyn. Ašies lygtis yra x = 0 Krypties lygtis yra y – a = 0 Latus tiesiosios žarnos ilgis = 4a

Toliau pateikiami stebėjimai, atlikti naudojant standartinę parabolės lygčių formą:

• Parabolė yra simetriška prieš savo ašį. Pavyzdžiui, y²= 4ax yra simetriška x ašies atžvilgiu, o x²= 4ay yra simetriškas y ašies atžvilgiu.

• Jei parabolė yra simetriška x ašiai, tada parabolė atsidaro į dešinę, jei x koeficientas yra teigiamas, ir į kairę, jei x koeficientas yra neigiamas.

• Jei parabolė yra simetriška y ašiai, tada parabolė atsidaro aukštyn, jei y koeficientas yra teigiamas, ir žemyn, jei y koeficientas yra neigiamas.

Toliau pateikiamos standartinės parabolės lygtys, kai simetrijos ašis yra lygiagreti x arba y ašiai, o viršūnė nėra pradžioje.

Parabolės lygtis	Parabolė	Parabolės parametrų formulės
(ir – k)2= 4a(x – h)	Horizontali parabolė	Viršūnė = (h, k) Fokusas = (h + a, k) Parabolė atsidaro į dešinę pusę. Ašies lygtis yra y = k Krypties lygtis x = h – a Latus tiesiosios žarnos ilgis = 4a
(ir – k)2= -4a(x – h)	Horizontali parabolė	Viršūnė = (h, k) Fokusas = (h – a, k) Parabolė atsidaro į kairę pusę. Ašies lygtis yra y = k Krypties lygtis yra x = h + a Latus tiesiosios žarnos ilgis = 4a
(x – h)2= 4a(y – k)	Vertikali parabolė	Viršūnė = (h, k) Fokusas = (h, k + a) Parabolė atsiveria į viršų. Ašies lygtis x = h Krypties lygtis yra y = k – a Latus tiesiosios žarnos ilgis = 4a
(x – h)2= -4a(y – k)	Vertikali parabolė	Viršūnė = (h, k) Fokusas = (h, k – a) Parabolė atsidaro žemyn. Ašies lygtis x = h Krypties lygtis yra y = k + a Latus tiesiosios žarnos ilgis = 4a

Parabolės išvedimo lygtis

Tegu P yra taškas parabolėje, kurios koordinatės yra (x, y). Pagal parabolės apibrėžimą taško P atstumas iki židinio (F) yra lygus to paties taško P atstumui iki parabolės krypties. Dabar panagrinėkime krypties tašką X, kurio koordinatės yra (-a, y).

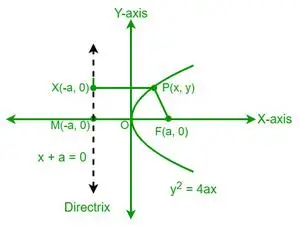
Iš parabolės ekscentriškumo apibrėžimo turime

e = PF/PX = 1

⇒ PF = PX

Židinio koordinatės yra (a, 0). Dabar, naudodamiesi koordinačių atstumo formule, galime rasti taško P (x, y) atstumą iki židinio F (a, 0).

PF = √[(x – a)²+ (ir – 0)²]

⇒ PF = √[(x – a)²+ ir²] ------ (1)

Krypties lygtis yra x + a = 0. Norėdami rasti PX atstumą, naudojame statmeno atstumo formulę.

PX = (x + a)/√[1²+0²]

⇒ PX = x +a —————— (2)

Mes jau žinome, kad PF = PX. Taigi, sulyginkite (1) ir (2) lygtis.

√[(x – a)²+ ir²] = (x + a)

Iš abiejų pusių padalydami kvadratu, gauname,

⇒ [(x – a)²+ ir²] = (x + a)²

⇒ x²+ a²– 2ax + y²= x²+ a²+ 2ax

⇒ ir²– 2ax = 2ax

⇒ ir²= 2ax + 2ax ⇒ ir ² = 4ax

Taigi, mes išvedėme parabolės lygtį. Panašiai galime išvesti kitų trijų parabolių standartines lygtis.

• ir²= -4ax
• x²= 4ay
• x²= -4ay

ir ² = 4ax ir ² = -4ax, x ² = 4ay ir x ² = -4ay yra standartinės parabolės lygtys.

Straipsniai, susiję su parabole:

• Apskritimo lygtis
• Elipsės lygtis
• Hiperbolės lygtis
• Parabolės taikymas realiame gyvenime

Parabolės lygties pavyzdžiai

1 pavyzdys: Raskite latus tiesiosios žarnos ilgį, židinį ir viršūnę, jei parabolės lygtis yra y ² = 12x.

Sprendimas:

Atsižvelgiant į

Parabolės lygtis yra y²= 12x

Palyginus pateiktą lygtį su standartine y forma²= 4ax

4a = 12

⇒ a = 12/4 = 3

Mes tai žinome,

Dešinė parabolės pusė = 4a = 4 (3) = 12

Dabar parabolės židinys = (a, 0) = (3, 0)

Duotos parabolės viršūnė = (0, 0)

2 pavyzdys: Raskite parabolės, kuri yra simetriška X ašiai ir eina per tašką (-4, 5), lygtį.

Sprendimas:

Atsižvelgiant į

Parabolė yra simetriška X ašiai ir jos viršūnė yra ištakoje.

Taigi lygtis gali būti y formos²= 4ax arba y²= -4ax, kur ženklas priklauso nuo to, ar parabolė atsidaro į kairę ar į dešinę pusę.

Parabolė turi atsidaryti į kairę, nes ji eina per (-4, 5), esantį antrajame kvadrante.

Taigi lygtis bus tokia: y²= -4ax

Pakeičiant (-4, 5) pirmiau pateiktoje lygtyje,

⇒ (5)²= -4a(-4)

⇒ 25 = 16a

⇒ a = 25/16

Todėl parabolės lygtis yra tokia: y²= -4(25/16)x (arba) 4m²= -25x.

3 pavyzdys: Raskite parabolės x židinio, ašies, krypties lygties ir tiesiosios žarnos latus koordinates ² = 16 m.

Sprendimas:

Atsižvelgiant į

Parabolės lygtis yra: x²= 16 m

Lyginant pateiktą lygtį su standartine forma x²= 4ay,

4a = 16 ⇒ a = 4

Koeficientas y yra teigiamas, todėl parabolė atsidaro aukštyn.

Be to, simetrijos ašis yra išilgai teigiamos Y ašies.

Vadinasi,

Parabolės židinys yra (a, 0) = (4, 0).

Krypties lygtis yra y = -a, ty y = -4 arba y + 4 = 0.

Latus tiesiosios žarnos ilgis = 4a = 4(4) = 16.

4 pavyzdys: Raskite tiesiosios žarnos, židinio ir viršūnės ilgį, jei parabolės lygtis yra 2(x-2) ² + 16 = m.

Sprendimas:

Atsižvelgiant į

Parabolės lygtis yra 2(x-2)²+ 16 = ir

Lyginant pateiktą lygtį su bendrąja parabolės lygtimi y = a(x – h)²+ k, gauname

a = 2

(h, k) = (2, 16)

Mes tai žinome,

Parabolės tiesiosios žarnos ilgis = 4a

= 4 (2) = 8

Dabar fokusuokite = (a, 0) = (2, 0)

Dabar viršūnė = (2, 16)

5 pavyzdys: parabolės lygtis yra x ² – 12x + 4y – 24 = 0, tada raskite jos viršūnę, židinį ir kryptį.

Sprendimas:

Atsižvelgiant į

Parabolės lygtis yra x²– 12x + 4m – 24 = 0

⇒ x²– 12x + 36 – 36 + 4m – 24 = 0

⇒ (x – 6)²+ 4 m. – 60 = 0

⇒ (x – 6)²= -4 (y + 15)

Gauta lygtis yra (x – h)²= -4a(y – k)

-4a = -4 ⇒ a = 1

Taigi, viršūnė = (h, k) = (6, – 15)

Fokusas = (h, k – a) = (6, -15-1) = (6, -16)

Krypties lygtis yra y = k + a

⇒ y = -15 + 1 ⇒ y = -14

⇒ y + 14 = 0

DUK apie parabolės lygtį

Kaip rasti standartinę parabolės lygtį?

Standartinė parabolės forma yra y²= 4ax arba x²= 4ay.

Kas yra normalioji parabolės lygtis?

Parabolės y normaliosios lygtis²= 4ax su nuolydžiu m pateikiama taip: y = mx – 2am – am ³

Kaip rasti parabolės viršūnę?

Duotajai parabolei: y = ax²+ bx + c jos viršūnę galima rasti naudojant formulę x = − b/2a. Prijunkite šią x reikšmę atgal į lygtį, kad rastumėte atitinkamą y koordinatę.

paaiškinti duomenų nepriklausomumą