Nuolydžio formulė naudojama linijos statumui arba nuolydžiui nustatyti. Tiesės nuolydžiui apskaičiuoti naudojamos taškų, esančių tiesėje, x ir y koordinatės. Y koordinatės pokytis, susijęs su x koordinačių pokyčiu, vadinamas linijos nuolydžiu ir paprastai vaizduojamas raide m.

Turinys

• Kas yra nuolydžio formulė?
• Šlaito formulė
• Nuolydžio formulės išvedimas
• Linijos nuolydžio (tiesios linijos) formulė
• Nuolydžio lygtis
• Nuolydžio formulės pavyzdys

Kas yra nuolydžio formulė?

Norint apskaičiuoti linijos nuolydį, reikalinga nuolydžio formulė. Tiesės nuolydžiui apskaičiuoti reikalingos tiesės taškų x ir y koordinatės. Y koordinačių pokyčio ir x koordinačių kitimo santykis vadinamas tiesės nuolydžiu.

Nuolydis (m) = y pokytis/x pokytis = Δy/Δx

Šlaito formulė

Matematikoje linijos nuolydis naudojamas norint nustatyti, kiek linija pasvirusi, t. y. linijos statumą. Norint nustatyti tiesės nuolydį, mums reikia tiesėje esančių taškų x ir y koordinačių. Nuolydžio formulė yra grynasis y koordinatės pokytis, padalytas iš grynojo x koordinatės pokyčio. Δy yra y koordinačių pokytis, o Δx yra x koordinačių pokytis. Taigi, y koordinačių pokyčio santykis su x koordinačių pokyčiu pateikiamas taip:

Nuolydis (m) = y pokytis/x pokytis = Δy/Δx

m = (ir ₂ - ir ₁ )/(x ₂ – x ₁ )

kur

• x₁ir x₂yra X ašies koordinatės
• ir₁ir y₂yra Y ašies koordinatės

Nuolydžio formulės išvedimas

Linijos nuolydžiui apskaičiuoti naudojamos tiesės x ir y koordinatės. Grynasis y koordinatės pokytis yra Δy, o grynasis x koordinatės pokytis yra Δx. Taigi y koordinatės pokytis x koordinatės pokyčio atžvilgiu gali būti parašytas taip,

m = Δy/Δx

kur,

• m yra nuolydis
• Δy yra y koordinačių pokytis
• Δx yra x koordinačių pokytis

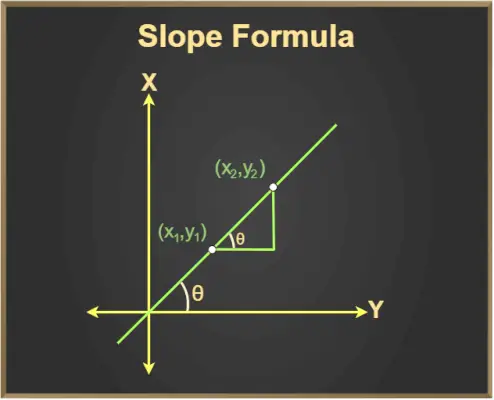
Žinome, kad tan θ taip pat yra linijos nuolydis, kur θ yra kampas, sudarytas linijos su teigiama x ašies kryptimi.

Ir, tan θ = aukštis/pagrindas

Kadangi aukštis / pagrindas tarp bet kurių dviejų nurodytų taškų = (y₂- ir₁)/(x₂– x₁)

Taigi, nuolydžio lygtis yra tokia, kad m = tan θ = Δy/Δx

Iš grafiko matome:

„Android“ kūrėjo režimo išjungimas

Δy = (y₂- ir₁)

Δx = (x₂– x₁)

Tada nuolydžio formulė pateikiama taip:

Nuolydis = m = (y ₂ - ir ₁ )/(x ₂ – x ₁ )

Linijos nuolydžio (tiesios linijos) formulė

• Mes tai žinome įdegis θ taip pat yra linijos nuolydis, todėl linijos nuolydis taip pat gali būti pavaizduotas kaip

Nuolydis (m) = tan θ = Δy/Δx

Kur i yra kampas, kurį sudaro linija w.r.t su teigiama X ašimi,

• Δy = y koordinačių pokytis,
• Δx = x koordinačių pokytis.

• Taip pat linijos nuolydį galime apibrėžti kaip kilimo santykį bėgimo atžvilgiu.

Nuolydis (m) = kilimas / bėgimas

• Tegul ax + by + c = 0 yra bendroji tiesės lygtis. Dabar linijos nuolydžio formulė pateikiama taip,

Nuolydis (m) = – x koeficientas / y koeficientas = -a/b

• Linijos nuolydžio pertraukos forma naudojant linijos lygtį pateikiama taip,

y = mx + c

Kur m yra tiesės nuolydis, o c yra linijos y susikirtimo taškas.

Nuolydžio lygtis

Linijos nuolydžiui nustatyti naudojama nuolydžio formulė. Lygtis, naudojama ieškant nuolydžio, parašyta taip:

m = tanθ = Δy/Δx = (y ₂ - ir ₁ )/(x ₂ – x ₁ )

aktorius Zeenat Aman

kur,

• m yra linijos nuolydis
• Δy yra y koordinačių skirtumas
• Δx yra x koordinačių skirtumas
• i yra kampas, sudarytas tiesės su teigiama x ašimi

Linijos su nuolydžiu m lygtis pateikiama taip,

y = mx + c

kur,

• m yra linijos nuolydis
• b yra linijos y susikirtimas

Skaityti daugiau,

apvalkalo rūšis

• Lygiagrečios linijos
• Šlaito perėmimo forma

Nuolydžio formulės pavyzdys

1 pavyzdys: Raskite tiesės, kurios koordinatės yra (3, 7) ir (5, 8), nuolydį.

Sprendimas:

Atsižvelgiant, (x₁, ir₁) = (3,7) ir (x₂, ir₂) = (5,8)

Nuolydžio formulė (m) = (y ₂ - ir ₁ )/(x ₂ – x ₁ )

⇒ m = (8 – 7)/(5 – 3) = 1/2

Vadinasi, nurodytos linijos nuolydis yra 1/2.

2 pavyzdys: nustatykite linijos, kurios koordinatės yra (7, -5) ir (2, -3), nuolydį.

Sprendimas:

Atsižvelgiant, (x₁, ir₁) = (7, -5) ir (x₂, ir₂) = (23)

Nuolydžio formulė (m) = (y ₂ - ir ₁ )/(x ₂ – x ₁ )

⇒ m = (-3 – (-5))/(2 – 7) = -2/5

Vadinasi, nurodytos linijos nuolydis yra -2/5

3 pavyzdys: Raskite a reikšmę, jei linijos, einančios per taškus (-4, a) ir (2, 5), nuolydis yra 3.

Sprendimas:

Atsižvelgiant, (x₁, ir₁) = (4,a) ir (x₂, ir₂) = (2, 5) ir nuolydis (m) = 3

Žinome, kad nuolydis (m) = (y ₂ - ir ₁ )/(x ₂ – x ₁ )

⇒ 3 = (5 – a)/(2 – 4)

⇒ 3 = (5 – a)/(-2)

⇒ -6 = 5 – a ⇒ a = 5 + 6 = 11

Taigi a reikšmė = 11

4 pavyzdys: jei tiesė sudaro 60° kampą su teigiama Y ašimi, kokia yra linijos nuolydžio vertė?

Sprendimas:

Pateikti duomenys, kampas, sudarytas iš linijos su teigiama y ašimi = 60°

eilutę į int java

Žinome, kad jei linija sudaro 60° kampą nuo teigiamos y ašies, tai ji sudaro (90° – 60° = 30°) kampą su x ašimi.

Todėl linijos nuolydžio vertė (m) = tan 30° = 1/√3

Vadinasi, linijos nuolydžio reikšmė = 1/√3.

5 pavyzdys: Sheela tikrino grafiką ir pastebėjo, kad kėlimas buvo 12 vienetų, o bėgimas – 4 vienetai. Dabar apskaičiuokite linijos nuolydį.

Sprendimas:

Pateiktais duomenimis, pakilimas = 12 vienetų ir paleidimas = 4 vienetai

Žinome, kad nuolydis (m) = kilimas/bėgimas

⇒ m = 12/4 = 3

Taigi nurodytos linijos nuolydis yra 3

6 pavyzdys: Raskite tiesės nuolydį 3x – 7y + 8 = 0.

Sprendimas:

Pateikti duomenys, tiesės lygtis = 3x – 7y + 8 = 0

Dabar palyginkite pateiktą su bendrąja linijos lygtimi, ty ax + by + c = 0

Todėl a = 3, b = -7 ir c = 8

Žinome, kad nuolydis (m) = – x koeficientas/y koeficientas = -a/b

⇒ m = -3/(-7) = 3/7

Vadinasi, nurodytos linijos nuolydis yra 3/7.

Praktiniai klausimai apie nuolydžio formulę

Q1. Apskaičiuokite linijos, einančios per taškus (2, 3) ir (5, 7), nuolydį

Q2. Duota tiesės lygtis: y = 3x – 11, koks jos nuolydis?

Q3. Jei tiesės nuolydis yra 5/6 ir ji eina per tašką (2, 5), kokia yra tiesės lygtis nuolydžio pertraukos forma?

4 klausimas. Apskaičiuokite tiesės, lygiagrečios tiesei (0, -3) ir (1, 11) nuolydį

pavasario inicializr

Q5. Jei linijos nuolydis neapibrėžtas, ką galite padaryti apie liniją?

DUK apie nuolydžio formulę

Kas yra linijos nuolydis?

Linijos nuolydis – tai tiesės statumo arba polinkio x-y plokštumoje reikšmė. Nuolydis apskaičiuojamas naudojant skirtingus metodus, priklausomai nuo to, ar pateikta tiesės lygtis, ar linijos taškų koordinatės.

Pagal kokią formulę galima rasti liestinės formulės nuolydį?

Linijos nuolydis apskaičiuojamas pagal pateiktą formulę. Tarkime, kad dviejų taškų, esančių tiesėje, koordinatės yra (x₁, ir₁)/(x_{2 ,}ir₂). Tada formulė pateikiama kaip Nuolydis = m = tan θ = (y ₂ - ir ₁ )/(x ₂ – x ₁ )

Kas yra nuolydžio formulės apibrėžimas?

Nuolydžio formulė apibrėžiama taip,

• Nuolydis = (y koordinatės pokytis) / (x koordinatės pokytis)
• Nuolydis = kilimas / bėgimas.

Koks yra grafiko formulės nuolydis?

Linijos nuolydis yra jos polinkio su teigiama x ašimi matas. Matematiškai nuolydis apibrėžiamas kaip pakilti per paleisti .