Sin Cos formulės trigonometrijoje: Trigonometrija, kaip rodo jos pavadinimas, yra trikampių tyrimas. Tai svarbi matematikos šaka, tirianti ryšį tarp stačiojo trikampio kraštinių ilgių ir kampų, taip pat padedanti nustatyti trūkstamus trikampio kraštinių ilgius arba kampus. Yra šeši trigonometriniai santykiai arba funkcijos: sinusas, kosinusas, liestinė, kosekantas, sekantas ir kotangentas, kur kosekantas, sekantas ir kotangentas yra abipusės kitų trijų funkcijų, t. y. sinuso, kosinuso ir liestinės, funkcijos.
Trigonometrinis santykis apibrėžiamas kaip stačiojo trikampio kraštinių ilgių santykis. Trigonometrija mūsų kasdieniame gyvenime naudojama įvairiose srityse. Tai padeda nustatyti kalvų ar pastatų aukštį. Jis taip pat naudojamas tokiose srityse kaip kriminologija, statyba, fizika, archeologija, laivų variklių inžinerija ir kt.
Šiame straipsnyje mes išnagrinėsime viską trigonometrijos formulės dažniausiai sin ir cos formulės su jų pavyzdžiais ir visų trigonometrijos formulių sąrašas.
Turinys
- Formulės trigonometrijoje
- Kai kurios pagrindinės Sin Cos formulės
- Sin Cos formulių lentelė
- Sin Cos formulių pavyzdžiai
- Praktikos problemos dėl Sin Cos formulių trigonometrijoje su pavyzdžiais
Formulės trigonometrijoje
Panagrinėkime stačiakampį trikampį XYZ, kur ∠Y = 90°. Tegul kampas viršūnėje Z yra θ. Kraštinė, esanti šalia θ, vadinama gretima, o priešinga θ – priešinga. Hipotenuzė yra priešinga stačiajam kampui arba ilgiausia stačiojo kampo pusė.
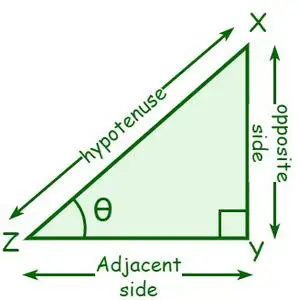
- sin θ = priešinga pusė/hipotenuzė
- cos θ = gretima pusė/hipotenūza
- tan θ = priešinga pusė/gretima pusė
- cosec θ = 1/sin θ = hipotenuzė / priešinga pusė
- sek θ = 1/ cos θ = hipotenūza/gretima pusė
- vaikiška lovelė θ = 1/ tan θ = gretima pusė / priešinga pusė
Sinuso formulė
Stačiakampio trikampio kampo sinusas yra priešingos kraštinės ilgio ir hipotenuzės ilgio santykis su nurodytu kampu. Sinuso funkcija vaizduojama kaip nuodėmė.
sin θ = priešinga pusė/hipotenuzė
Kosinuso formulė
Stačiakampio trikampio kampo kosinusas yra gretimos kraštinės ilgio ir hipotenuzės ilgio santykis su nurodytu kampu. Kosinuso funkcija vaizduojama kaip cos.
objektas java programavimecos θ = gretima pusė/hipotenūza
Kai kurios pagrindinės Sin Cos formulės
Sinuso ir kosinuso funkcijos kvadrantuose
- Sinuso funkcija yra teigiama pirmame ir antrame kvadrantuose, o neigiama trečiame ir ketvirtame kvadrantuose.
- Pirmajame ir ketvirtajame kvadrantuose kosinuso funkcija yra teigiama, o antrajame ir trečiame – neigiama.
Laipsniai
Kvadrantas
Sinuso funkcijos ženklas
Kosinuso funkcijos ženklas
0° iki 90°
1 kvadrantas
+ (teigiamas)
+ (teigiamas)
90° iki 180°
2 kvadrantas
+ (teigiamas)
– (neigiamas)
180° iki 270°
3 kvadrantas
– (neigiamas)
– (neigiamas)
270° iki 360°
4-asis kvadrantas
– (neigiamas)
+ (teigiamas)
Sinuso ir kosinuso funkcijų neigiamo kampo tapatybė
- Neigiamojo kampo sinusas visada lygus neigiamam kampo sinusui.
sin (– θ) = – sin θ
- Neigiamo kampo kosinusas visada lygus kampo kosinusui.
cos (– θ) = cos θ
Ryšys tarp sinuso ir kosinuso funkcijos
sin θ = cos (90° – θ)
Sinuso ir kosinuso funkcijų abipusės funkcijos
- Kosekanto funkcija yra sinusinės funkcijos abipusė funkcija.
cosec θ = 1/sin θ
- Sekanto funkcija yra kosinuso funkcijos abipusė funkcija.
sek θ = 1/cos θ
Pitagoro tapatybė
be 2 θ + cos 2 θ = 1
Sinuso ir kosinuso funkcijų periodinės tapatybės
sin (θ + 2nπ) = sin θ
cos (θ + 2nπ) = cos θ
Dvigubo kampo formulės sinuso ir kosinuso funkcijoms
sin 2θ = 2 sin θ cos θ
cos 2θ = cos 2 θ – nuodėmė 2 θ = 2 cos 2 θ – 1 = 1 – 2 nuodėmė 2 i
Sinuso ir kosinuso funkcijų pusės kampo tapatybės
sin (θ/2) = ±√[(1 – cos θ)/2]
cos (θ/2) = ±√[(1 + cos θ)/2]
Trigubo kampo tapatybės sinuso ir kosinuso funkcijoms
sin 3θ = 3 sin θ – 4 sin 3 i
cos 3θ = 4cos 3 θ – 3 cos θ
Sumos ir skirtumo formulės
- Sinuso funkcija
nuodėmė (A + B) = nuodėmė A cos B + cos A nuodėmė B
sin (A – B) = sin A cos B – cos A nuodėmė B
- Kosinuso funkcija
cos (A + B) = cos A cos B – sin A sin B
cos (A – B) = cos A cos B + sin A sin B
Sinuso dėsnis arba sinuso taisyklė
Sinuso taisyklės sinusų dėsnis yra trigonometrinis dėsnis, nurodantis santykį tarp trikampio kraštinių ilgių ir kampų.

a/sin A = b/sin B = c/sin C
Kur a, b ir c yra trikampio ABC trijų kraštinių ilgiai, o A, B ir C yra kampai.
Kosinusų dėsnis
Kosinuso taisyklės kosinusų dėsnis naudojamas trūkstamiems arba nežinomiems trikampio kampams arba kraštinių ilgiams nustatyti.

a 2 = b 2 + c 2 – 2bc cos A
b 2 = c 2 + a 2 – 2ca cos B
c 2 = a 2 + b 2 – 2ab cos C
Kur a, b ir c yra trikampio ABC trijų kraštinių ilgiai, o A, B ir C yra kampai.
Sin Cos formulių lentelė
Čia yra Sin ir Cos formulių lentelė / sąrašas įvairiems kampams laipsniais ir radianais:
Sin Cos formulių sąrašas
| Kampas (laipsniais) | Kampas (radianais) | nuodėmė i | cos θ |
|---|---|---|---|
| 0° | 0 | 0 | 1 |
| 30° | p/6 | 1/2 | _3/2 |
| 45° | p/4 | 1/√2 | 1/√2 |
| 60° | p/3 | √3/2 | 1/2 |
| 90° | p/2 | 1 | 0 |
| 120° | 2p/3 | √3/2 | -1/2 |
| 150° | 5p/6 | 1/2 | -√3/2 |
| 180° | Pi | 0 | -1 |
Sin Cos formulių pavyzdžiai
1 uždavinys: jei cos α = 24/25, tada raskite sin α reikšmę.
Sprendimas:
Atsižvelgiant į
cos α = 24/25
Iš mūsų turimų pitagoriečių tapatybių;
cos2θ + nuodėmė2θ = 1
(24/25)2+ be2α = 1
be2α = 1 – (24/25)2
be2α = 1 – (576/625) = (625 – 576)/625
be2α = (625 – 576)/625 = 49/626
sin α = √49/625 = ±7/25
Vadinasi, sin α = ±7/25.
2 uždavinys: įrodykite sin 2A ir cos 2A formules, jei ∠A= 30°.
sumažinimo perbraukimas
Sprendimas:
Duota, ∠A= 30°
Mes tai žinome,
1) sin 2A = 2 sin A cos A
sin 2(30°) = 2 sin 30° cos 30°
sin 60° = 2 × (1/2) × (√3/2) {Kadangi sin 30° = 1/2, cos 30° = √3/2 ir sin 60° = √3/2}
√3/2 = √3/2
L.H.S = R.H.S
2) cos 2A = 2cos2A – 1
cos 2(30°) = 2cos2(30°) – 1
cos 60° = 2 (√3/2)2– 1 = 3/2 – 1 {Kadangi cos 60° = 1/2 ir cos 30° = √3/2}
1/2 = 1/2
L.H.S = R.H.S
Taigi įrodyta.
3 uždavinys: Raskite cos x reikšmę, jei tan x = 3/4.
Sprendimas:
Duota, įdegis x = 3/4
Mes tai žinome,
įdegis x = priešinga pusė / gretima pusė = 3/4
Norėdami rasti hipotenuzą, naudojame Pitagoro teoremą:
hipotenuzė2= priešingai2+ gretimas2
H2= 32+ 42
H2= 9 + 16 = 25
H = √25 = 5
Dabar cos x = gretima pusė / hipotenuzė
cos x = 4/5
Taigi cos x reikšmė yra 4/5.
4 uždavinys: raskite ∠C (laipsniais) ir ∠A (laipsniais), jei ∠B = 45°, BC = 15 colių ir AC = 12 colių.

Sprendimas:
Duota: ∠B = 45°, BC = a = 15 colių ir AC = b = 12 colių.
Iš sinusų dėsnio mes turime
a/sin A = b/sin B = c/sin C
⇒ a/sin A = b/sin B
⇒ 15/sin A = 12/sin 45°
⇒ 15/sin A = 12/(1/√2)
⇒ 15/sin A = 12√2 = 16,97
⇒ be A = 15/16,97 = 0,8839
⇒ ∠A = nuodėmė-1(0,8839) = 62,11°
Žinome, kad trikampio vidinių kampų suma yra 180°.
Taigi, ∠A + ∠B + ∠C = 180°
⇒ 62,11° + 45° + ∠C = 180°
⇒ ∠C = 180° – (62,11° + 45°) = 72,89°
Vadinasi, ∠A = 62,11° ir ∠C = 72,89°.
5 uždavinys: Įrodykite kosinuso funkcijos pusės kampo tapatybes.
Sprendimas:
Kosinuso funkcijos pusės kampo tapatybė yra tokia:
cos (θ/2) = ±√[(1 + cos θ)/2]
Iš dvigubo kampo tapatybių turime,
cos 2A = 2 cos2A – 1
Dabar pakeiskite A θ/2 abiejose pusėse
⇒ cos 2(θ/2) = 2 cos2(i/2) – 1
⇒ cos θ = 2 cos2(i/2) – 1
⇒ 2cos2(θ/2) = cos θ + 1
⇒ cos2(θ/2) = (cos θ + 1)/2
⇒ cos (θ/2) = ±√[(1 + cos θ)/2]
Taigi įrodyta.
Praktikos problemos dėl Sin Cos formulių trigonometrijoje su pavyzdžiais
1. Duota sin θ = 3/5. Raskite cos θ.
2. Įrodykite tapatybę sin(2A) = 2 sinA cosA, jei A=45∘.
3. Jei cos α = 5/13. Raskite nuodėmę(2a).
4. Išspręskite θ, jei sin θ = cos(90∘−θ).
5. Jei tan β = 2. Raskite sin β ir cos β naudodami Pitagoro tapatybę.
DUK apie Sin Cos formules trigonometrijoje su pavyzdžiais
Kokios yra pagrindinės trigonometrijos sinuso ir kosinuso formulės?
Pagrindinės sinuso ir kosinuso formulės yra sin θ = priešprieša/hipotenūza ir cos θ = gretimas/hipotenūza, kur θ yra stačiakampio trikampio kampas.
Kaip rasti specialių kampų sinusus ir kosinusus?
Specialūs kampai, tokie kaip 0∘, 30∘, 45∘, 60∘ ir 90∘, turi specifines sinuso ir kosinuso reikšmes, kurias galima prisiminti naudojant trigonometrines lenteles arba vienetinio apskritimo sąvokas.
Koks yra sinuso ir kosinuso funkcijų ryšys?
Sinuso ir kosinuso funkcijos yra susijusios tapatybe sin θ = cos(90∘- θ) ir pitagoriečių tapatybę be 2 θ+cos 2 θ = 1.
Kaip naudojate sinuso ir kosinuso dvigubo kampo formules?
Dvigubo kampo formulės yra sin(2θ) = 2sinθcosθ ir cos(2θ)=cos 2 θ – nuodėmė 2 i. Jie naudojami dvigubų kampų trigonometrinėms funkcijoms išreikšti pavieniais kampais.
Kaip rasti skirtingų kvadrantų kampų sinuso ir kosinuso vertes?
Sinuso ir kosinuso funkcijų ženklai priklauso nuo kvadranto, kuriame yra kampas:
- Pirmasis kvadrantas: sin θ> 0 ir cos θ> 0
- Antrasis kvadrantas: sin θ> 0 ir cos θ < 0
- Trečiasis kvadrantas: sinθ <0 ir cosθ < 0
- Ketvirtasis kvadrantas: sinθ 0
