Kvantilio-kvantilės (q-q diagramos) diagrama yra grafinis metodas, leidžiantis nustatyti, ar duomenų rinkinys atitinka tam tikrą tikimybių pasiskirstymą, ar du duomenų pavyzdžiai yra iš to paties. gyventojų arba ne. Q-Q diagramos yra ypač naudingos vertinant, ar duomenų rinkinys yra paprastai paskirstytas arba jei jis atitinka kitą žinomą pasiskirstymą. Jie dažniausiai naudojami statistikoje, duomenų analizėje ir kokybės kontrolėje, siekiant patikrinti prielaidas ir nustatyti nukrypimus nuo numatomų paskirstymų.
Kvantiliai ir procentiliai
Kvantiliai yra taškai duomenų rinkinyje, padalijantys duomenis į intervalus, kuriuose yra vienodos tikimybės arba viso skirstinio proporcijos. Jie dažnai naudojami apibūdinti duomenų rinkinio sklaidą ar pasiskirstymą. Dažniausiai naudojami kvantiliai:
- Mediana (50 procentilis) : mediana yra vidutinė duomenų rinkinio reikšmė, kai jis suskirstytas nuo mažiausio iki didžiausio. Jis padalija duomenų rinkinį į dvi lygias dalis.
- Kvartiliai (25, 50 ir 75 procentiliai) : kvartiliai padalija duomenų rinkinį į keturias lygias dalis. Pirmasis kvartilis (Q1) yra vertė, žemiau kurios patenka 25 % duomenų, antrasis kvartilis (Q2) yra mediana, o trečiasis kvartilis (Q3) yra vertė, žemiau kurios patenka 75 % duomenų.
- Procentiliai : Procentiliai yra panašūs į kvartilius, bet padalija duomenų rinkinį į 100 lygių dalių. Pavyzdžiui, 90 procentilis yra vertė, žemiau kurios patenka 90 % duomenų.
Pastaba:
- q-q diagrama yra pirmosios duomenų rinkinio kvantilių ir antrojo duomenų rinkinio kvantilių diagrama.
- Nuorodų tikslais taip pat nubrėžta 45 % linija; Dėl jei imtys yra iš tos pačios populiacijos, taškai yra išilgai šios linijos.
Normalus skirstinys:
Normalusis skirstinys (dar žinomas kaip Gauso skirstinio varpo kreivė) yra nuolatinis tikimybių pasiskirstymas, atspindintis pasiskirstymą, gautą iš atsitiktinai sugeneruotų realių verčių.
. 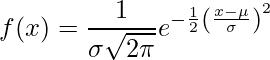

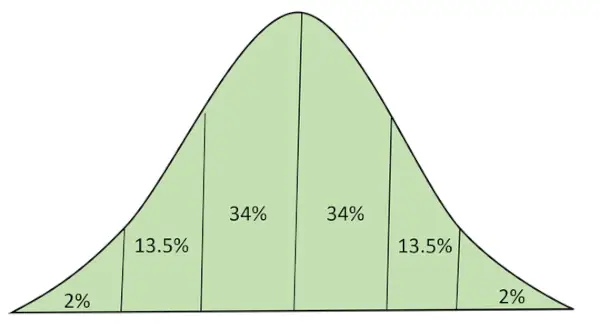
Normalus pasiskirstymas su plotu po kreive
Kaip nupiešti Q-Q brėžinį?
Norėdami nubrėžti kvantilio-kvantilio (Q-Q) diagramą, galite atlikti šiuos veiksmus:
- Surinkite duomenis : surinkite duomenų rinkinį, kuriam norite sukurti Q-Q diagramą. Įsitikinkite, kad duomenys yra skaitiniai ir sudaro atsitiktinę imtį iš dominančios populiacijos.
- Rūšiuoti duomenis : sutvarkykite duomenis didėjimo arba mažėjimo tvarka. Šis žingsnis yra būtinas norint tiksliai apskaičiuoti kvantinius.
- Pasirinkite teorinį pasiskirstymą : nustatykite teorinį pasiskirstymą, su kuriuo norite palyginti savo duomenų rinkinį. Įprasti pasirinkimai apima normalųjį pasiskirstymą, eksponentinį pasiskirstymą arba bet kokį kitą paskirstymą, kuris gerai atitinka jūsų duomenis.
- Apskaičiuokite teorinius kvantelius : Apskaičiuokite pasirinkto teorinio skirstinio kvantilius. Pavyzdžiui, jei lyginate su normaliuoju skirstiniu, norėdami rasti numatomus kvantilius, naudosite normalaus skirstinio atvirkštinio kumuliacinio skirstinio funkciją (CDF).
- Braižybos :
- Nubraižykite surūšiuotas duomenų rinkinio reikšmes x ašyje.
- Nubraižykite atitinkamus teorinius kvantilius y ašyje.
- Kiekvienas duomenų taškas (x, y) reiškia stebimų ir numatomų verčių porą.
- Prijunkite duomenų taškus, kad vizualiai patikrintumėte ryšį tarp duomenų rinkinio ir teorinio paskirstymo.
Q-Q siužeto interpretacija
- Jei taškai diagramoje patenka maždaug išilgai tiesia linija, tai rodo, kad jūsų duomenų rinkinys atitinka numatytą pasiskirstymą.
- Nukrypimai nuo tiesės rodo nukrypimus nuo numanomo pasiskirstymo, todėl reikia tolesnio tyrimo.
Pasiskirstymo panašumo tyrimas naudojant Q-Q diagramas
Pasiskirstymo panašumo tyrimas naudojant Q-Q diagramas yra pagrindinė statistikos užduotis. Dviejų duomenų rinkinių palyginimas, siekiant nustatyti, ar jie kilę iš to paties paskirstymo, yra gyvybiškai svarbus įvairiems analitiniams tikslams. Kai galioja bendro pasiskirstymo prielaida, duomenų rinkinių sujungimas gali pagerinti parametrų, pvz., vietos ir masto, įvertinimo tikslumą. Q-Q sklypai, trumpiniai kvantiliniai-kvantiliai, siūlo vizualų metodą pasiskirstymo panašumui įvertinti. Šiuose diagramose vieno duomenų rinkinio kvantiliai atvaizduojami pagal kito duomenų rinkinio kvantilius. Jei taškai glaudžiai sutampa išilgai įstrižainės linijos, tai rodo pasiskirstymo panašumą. Nukrypimai nuo šios įstrižainės linijos rodo pasiskirstymo charakteristikų skirtumus.
Nors tokie testai kaip chi kvadratas ir Kolmogorovas-Smirnovas testai gali įvertinti bendrus pasiskirstymo skirtumus, Q-Q diagramos suteikia niuansų perspektyvą tiesiogiai lyginant kvantilius. Tai leidžia analitikams įžvelgti konkrečius skirtumus, pvz., vietos poslinkius ar masto pokyčius, kurie gali būti nepastebimi vien iš formalių statistinių testų.
Python Q-Q brėžinio įgyvendinimas
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate example data> np.random.seed(>0>)> data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Create Q-Q plot> stats.probplot(data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Normal Q-Q plot'>)> plt.xlabel(>'Theoretical quantiles'>)> plt.ylabel(>'Ordered Values'>)> plt.grid(>True>)> plt.show()> |
>
>
Išvestis:
Q-Q siužetas
Čia, kadangi duomenų taškai apytiksliai eina tiesia linija Q-Q diagramoje, tai rodo, kad duomenų rinkinys atitinka numanomą teorinį pasiskirstymą, kurį šiuo atveju manėme kaip normalųjį pasiskirstymą.
Q-Q siužeto privalumai
- Lankstus palyginimas : Q-Q diagramos gali palyginti skirtingų dydžių duomenų rinkinius be reikalaujama vienodo imties dydžio.
- Analizė be matmenų : jie yra be matmenų, todėl tinka duomenų rinkiniams lyginti su skirtingi vienetai ar svarstyklės.
- Vizualinė interpretacija : pateikia aiškų vaizdinį duomenų paskirstymo vaizdą, palyginti su teoriniu paskirstymu.
- Jautrus nukrypimams : lengvai aptinka nukrypimus nuo numanomų paskirstymų ir padeda nustatyti duomenų neatitikimus.
- Diagnostikos įrankis : Padeda įvertinti paskirstymo prielaidas, identifikuoti nuokrypius ir suprasti duomenų modelius.
Kvantilės-kvantilės brėžinio taikymai
Kvantilės-kvantilės grafikas naudojamas šiems tikslams:
- Paskirstymo prielaidų vertinimas : Q-Q diagramos dažnai naudojamos vizualiai patikrinti, ar duomenų rinkinys atitinka tam tikrą tikimybių pasiskirstymą, pvz., normalųjį pasiskirstymą. Palyginus stebimų duomenų kvantilius su tariamo skirstinio kvantiliais, galima aptikti nukrypimus nuo numanomo skirstinio. Tai labai svarbu atliekant daugelį statistinių analizių, kur pasiskirstymo prielaidų pagrįstumas turi įtakos statistinių išvadų tikslumui.
- Nukrypimų aptikimas : nukrypimai yra duomenų taškai, kurie labai skiriasi nuo likusio duomenų rinkinio. Q-Q diagramos gali padėti nustatyti išskirtines vertes, atskleidžiant duomenų taškus, kurie toli nuo numatomo pasiskirstymo modelio. Nukrypimai gali būti rodomi kaip taškai, nukrypstantys nuo numatomos tiesės brėžinyje.
- Paskirstymų palyginimas : Q-Q diagramas galima naudoti norint palyginti du duomenų rinkinius, kad pamatytumėte, ar jie yra iš to paties skirstinio. Tai pasiekiama brėžiant vieno duomenų rinkinio kvantilius ir kito duomenų rinkinio kvantilius. Jei taškai patenka maždaug išilgai tiesios linijos, tai rodo, kad du duomenų rinkiniai yra sudaryti iš to paties skirstinio.
- Normalumo vertinimas : Q-Q diagramos ypač naudingos vertinant duomenų rinkinio normalumą. Jei duomenų taškai diagramoje yra arti tiesios linijos, tai rodo, kad duomenų rinkinys yra maždaug normaliai pasiskirstęs. Nukrypimai nuo linijos rodo nukrypimus nuo normalumo, todėl gali prireikti tolesnio tyrimo arba neparametrinių statistinių metodų.
- Modelio patvirtinimas : Tokiose srityse, kaip ekonometrija ir mašininis mokymasis, Q-Q diagramos naudojamos nuspėjamiesiems modeliams patvirtinti. Palyginus stebimų atsakymų kvantilius su modelio prognozuojamais kvantiliais, galima įvertinti, kaip modelis atitinka duomenis. Nukrypimai nuo numatyto modelio gali rodyti sritis, kuriose modelį reikia tobulinti.
- Kokybės kontrolė : Q-Q diagramos naudojamos kokybės kontrolės procesuose, kad būtų galima stebėti išmatuotų ar stebimų verčių pasiskirstymą laikui bėgant arba skirtingose partijose. Nukrypimai nuo numatytų schemos modelių gali reikšti pagrindinių procesų pokyčius, o tai paskatins tolesnius tyrimus.
Q-Q brėžinių tipai
Yra keletas Q-Q diagramų tipų, dažniausiai naudojamų statistikoje ir duomenų analizėje, kiekvienas pritaikytas skirtingiems scenarijams ar tikslams:
- Normalus skirstinys : simetriškas skirstinys, kuriame Q-Q diagramoje būtų rodomi taškai maždaug išilgai įstrižinės linijos, jei duomenys atitinka normalųjį pasiskirstymą.
- Dešinysis paskirstymas : pasiskirstymas, kuriame Q-Q diagramoje būtų rodomas modelis, kuriame stebimi kvantiliai nukrypsta nuo tiesios linijos link viršutinio galo, o tai rodo ilgesnę uodegą dešinėje.
- Paskirstymas į kairę : pasiskirstymas, kuriame Q-Q diagrama parodytų modelį, kai stebimi kvantiliai nukrypsta nuo tiesios linijos apatinio galo link, o tai rodo ilgesnę uodegą kairėje pusėje.
- Nepakankamas paskirstymas : pasiskirstymas, kuriame Q-Q diagrama parodytų, kad stebėti kvantiliai yra glaudžiau susitelkę aplink įstrižainę, palyginti su teoriniais kvantiliais, o tai rodo mažesnę dispersiją.
- Per daug išsklaidytas paskirstymas : pasiskirstymas, kuriame Q-Q diagramoje stebimi kvantai būtų labiau išsibarstę arba nukrypę nuo įstrižainės linijos, o tai rodo didesnę dispersiją arba sklaidą, palyginti su teoriniu pasiskirstymu.
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate a random sample from a normal distribution> normal_data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Generate a random sample from a right-skewed distribution (exponential distribution)> right_skewed_data>=> np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from a left-skewed distribution (negative exponential distribution)> left_skewed_data>=> ->np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from an under-dispersed distribution (truncated normal distribution)> under_dispersed_data>=> np.random.normal(loc>=>0>, scale>=>0.5>, size>=>1000>)> under_dispersed_data>=> under_dispersed_data[(under_dispersed_data>>>) & (under_dispersed_data <>1>)]># Truncate> # Generate a random sample from an over-dispersed distribution (mixture of normals)> over_dispersed_data>=> np.concatenate((np.random.normal(loc>=>->2>, scale>=>1>, size>=>500>),> >np.random.normal(loc>=>2>, scale>=>1>, size>=>500>)))> # Create Q-Q plots> plt.figure(figsize>=>(>15>,>10>))> plt.subplot(>2>,>3>,>1>)> stats.probplot(normal_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Normal Distribution'>)> plt.subplot(>2>,>3>,>2>)> stats.probplot(right_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Right-skewed Distribution'>)> plt.subplot(>2>,>3>,>3>)> stats.probplot(left_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Left-skewed Distribution'>)> plt.subplot(>2>,>3>,>4>)> stats.probplot(under_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Under-dispersed Distribution'>)> plt.subplot(>2>,>3>,>5>)> stats.probplot(over_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Over-dispersed Distribution'>)> plt.tight_layout()> plt.show()> |
>
>
Išvestis:
Q-Q diagrama skirtingiems skirstiniams
kelias nustatytas java
