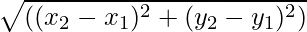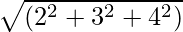VEKTORIAUS DYDIS – APIBRĖŽIMAS, FORMULĖ, PAVYZDŽIAI IR DUK

Vektoriniai dydžiai yra dydžiai, turintys ir kryptį, ir dydį. Vektoriaus dydis yra vektoriaus ilgis. Jis pateikiamas skaitine vektoriaus verte ir, kadangi jis reiškia vektoriaus ilgį, jis visada yra teigiamas. Bet kokiam vektoriui 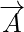overrightarrow{A} jo dydis pavaizduotas kaip .

Sužinokime daugiau apie vektoriaus dydį, jo formulę, pavyzdžius ir kitus šiame straipsnyje.

Turinys

Koks yra vektoriaus dydis?
Vektorinės formulės dydis
Vektoriaus kryptis
Kaip rasti vektoriaus dydį?
Išspręsti pavyzdžiai

Koks yra vektoriaus dydis?

Vektoriaus dydis apibrėžiamas kaip vektoriaus ilgis. Kadangi vektoriaus dydis rodo vektoriaus ilgį, jis visada yra teigiamas. Bet kurio vektoriaus A jo dydis vaizduojamas kaip |A|. Tarkime, kad vektorius apibrėžiamas kaip xi + yj, tada jo dydis apibrėžiamas kaip kvadratinė šaknis iš atskirų dėmenų kvadratų sumos. Vektoriaus dydis parodo vektoriaus ilgį, ty reikšmę arba vektoriaus poveikį.

Pavyzdžiui, jei objektą veikia 5i N jėga, tada jos dydis yra 5 N, o tai reiškia, kad taikomos jėgos stiprumas yra 5 N, ir aš' 5i reiškia, kad jis taikomas teigiama x kryptimi.

Vektorinės formulės dydis

Yra įvairių būdų, kaip apskaičiuoti vektoriaus dydį. Remdamiesi pateiktais duomenimis, naudokite kitokią formulę, kad surastumėte vektoriaus dydį. Vektoriaus A dydis atvaizduojamas naudojant modulio operatorių, ty |A|

Yra įvairių formulių, kurios naudojamos vektoriaus dydžiui skaičiuoti. Toliau pateiktame paveikslėlyje parodytos svarbios formulės, naudojamos vektoriaus dydžiui nustatyti.

Toliau pateikiami būdai, kaip apskaičiuoti dydį.

Jei jiems pateikiamas vektorius Ā = xi+ yĵ + zk̂, tada vektoriaus Ā dydį galima apskaičiuoti naudojant žemiau pateiktą formulę

Vektoriaus Ā dydis (|A|) = √(x ² + ir ² +z ² )

Jei pradžios taško vektorius yra (x₁, ir₁), o vektoriaus galinis taškas yra tarkim (x₂, ir₂) pateikiami tada vektoriaus dydis duoda,

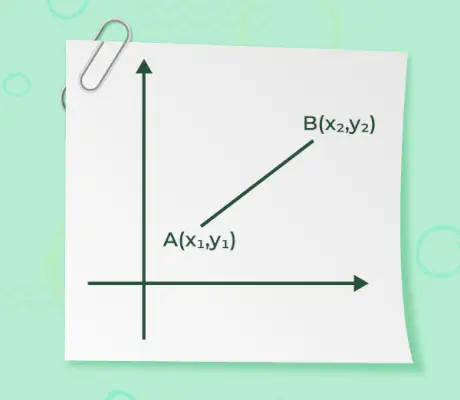
Vektoriaus dydis, kai nurodomi vektoriaus pradžios ir pabaigos taškai, yra ne kas kita, kaip atstumas tarp taškų. Didumo radimo formulė pateikiama pagal

= $sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}$

Jei kuris nors vektoriaus pradžios arba pabaigos taškas yra o(0, 0), o kitas taškas yra A(x, y) kaip nurodyta žemiau esančiame paveikslėlyje,

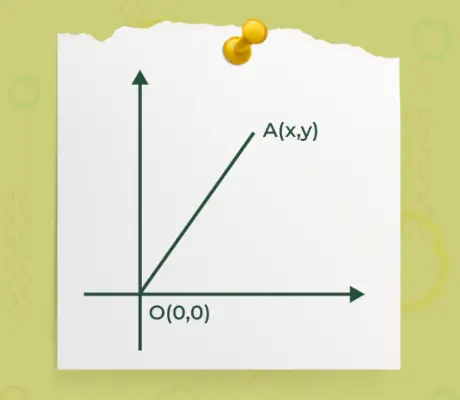
Vektoriaus dydis, jei nurodytas vienas taškas ir pradžia

Tada formulė, kaip rasti vektoriaus dydį, kai vienas iš vektoriaus galų yra pradžioje, yra pateikta

|Ā| = √(x ² +y ² )

Vektoriaus kryptis

Vektoriniai dydžiai yra dydžiai, turintys ir dydžius, ir kryptis. Vektoriaus kiekio kryptis reiškia, kuria kryptimi taikomas vektoriaus dydis. Jis apibrėžiamas kaip kampas, kurį vektorius sudaro su horizontalia linija arba x ašimi. Jį pavaizduoja simbolis a .

Žemiau esančiame paveikslėlyje parodyta rodyklė, kuri naudojama vektoriaus krypčiai parodyti.

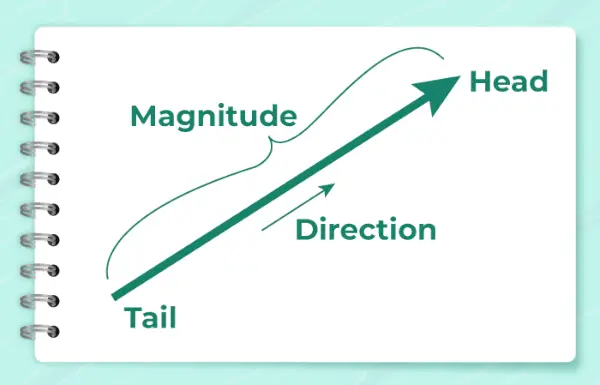
Jis apskaičiuojamas pagal formulę,

α = įdegis ^-1 (y/x)
javascript pasauliniai kintamieji

Vektoriui, sugeneruotam pagal koordinates (x₁, ir₁) ir (x₂, ir₂) jų kryptis nurodoma formule,

α = įdegis ^-1 [(ir ₂ - ir ₁ )/(x ₂ – x ₁ )]

Kaip rasti vektoriaus dydį?

Vektoriaus dydis apskaičiuojamas naudojant toliau aprašytus veiksmus,

1 žingsnis: Nustatykite vektoriaus komponentus x, y ir z.

2 žingsnis : Raskite visų x, y ir z komponentų kvadratą.

3 veiksmas: Pridėkite visus kvadratus, rastus 2 veiksme.

4 veiksmas: Raskite 3 veiksme gautos sumos kvadratinę šaknį.

Po 4 žingsnio gauta reikšmė yra nurodyto vektoriaus dydis.

Pavyzdys: Raskite vektoriaus A = 3i + 4j dydį

java konvertuoti char į eilutę

Sprendimas:

Vektoriaus A dydis apskaičiuojamas naudojant aukščiau aptartus veiksmus.

1 žingsnis: Palyginus A = 3i + 4j su xi + yj gauname x = 3 ir y = 4

2 žingsnis: x²= 3²= 9 ir y²= 4²= 16

3 veiksmas: x²+ ir²= 9 + 16 = 25

4 veiksmas: √(25) = 5

Taigi vektoriaus A = 3i + 4j dydis yra 5 vienetai.

Išvada

Apibendrinant galima pasakyti, kad vektoriaus dydis parodo, kokio ilgio vektorius yra. Ši koncepcija yra labai svarbi daugelyje sričių, pvz., fizikos, inžinerijos ir kompiuterių mokslo, nes ji padeda išmatuoti tokius dalykus kaip greitis, jėga ir judėjimo kryptis. Suprasdami vektorių dydį, galime geriau analizuoti ir spręsti praktines problemas, todėl tai yra pagrindinė žinių dalis visiems, dirbantiems su skaičiais ir matavimais realiose programose.

Skaityti daugiau,

Skaliarinis ir vektorius
Vektorinės operacijos
Kaip apskaičiuoti vieneto vektorių?

Išspręsti vektoriaus dydžio pavyzdžiai

1 pavyzdys: Raskite vektoriaus Ā = 2i + 3ĵ + 4k dydį.

Sprendimas:

„Java“ eilutėje yra

Atsižvelgiant į

Ā = 2i + 3ĵ + 4k

Didumas |A| = $sqrt{(2^2+3^2+4^2)}$

=
= √29
= 5,38

Vektoriaus dydis 2i+3ĵ+4k yra 5.38 vienetas

2 pavyzdys: Raskite vektoriaus Ā = 3i + 3ĵ – 6k dydį

Sprendimas:

Duota

Ā = 3i + 3ĵ – 6k

Didumas |A| = $sqrt{(3^2+3^2+(-6)^2)}$

=
= √54
= 7,35

Vektoriaus dydis 3i+ 3ĵ – 6k yra 7.35 vienetas.

3 pavyzdys: Raskite vektoriaus dydį, jei vektoriaus pradžios taškas yra (3, 4), o pabaigos taškas yra (6, 2).

Sprendimas:

Atsižvelgiant į

(x₁, ir₁) = (3, 4)
(x₂, ir₂) = (6, 2)

|Ā|= $sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}$

= $sqrt{((6-3)^2+(2-4)^2)}$
= √(3²+ (-2)²)
= √(9+4)
= √13 = 3,6

Taigi duoto vektoriaus dydis yra 3.6 vienetas.

4 pavyzdys: Raskite vektoriaus dydį, jei vektoriaus pradžios taškas yra (2, 1, 4), o pabaigos taškas yra (5, 2, 6).

Sprendimas:

Atsižvelgiant į

(x₁, ir₁, Su₁) = (2, 1, 4)

(x₂, ir₂, Su₂) = (5, 2, 6)

|Ā| = $sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}$

= $sqrt{((5-2)^2+(2-1)^2+(6-4)^2)}$
=
= √(9 +1 + 4)
= √14 = 3,74

Taigi duoto vektoriaus dydis yra 3.74 vienetas.

5 pavyzdys: koks yra vektoriaus, kuris prasideda pradžios ir pabaigos taške (3, 4), dydis.

Sprendimas:

Atsižvelgiant į

Vektoriaus pradžios taškas yra O(0, 0)
java maišant į int

Pabaigos taškas (x, y) = (3, 4)

Vektoriaus dydis (|Ā|) = √(x²+y²)

= √(3²+ 4²)
= √(9 + 16)
= √25 = 5

Taigi duoto vektoriaus dydis yra 5 vienetas.

6 pavyzdys: Raskite vektoriaus, kurio vienas iš galinių taškų yra pradžios taške, o kitas – (1, 4, 3), dydį.

Sprendimas:

Atsižvelgiant į

Vektoriaus pabaigos taškas yra O(0, 0)

Kitas taškas (x, y, z) = (1, 4, 3)

Vektoriaus dydis (|Ā|) = √(x²+y²+z²)

= $sqrt{(1^2+4^2+3^2)}$
=
= √26 = 5,09

Taigi duoto vektoriaus dydis yra 5.09 vienetas.
suskaidytas java

DUK apie vektoriaus dydį

Koks yra vektorinės formulės dydis?

Vektoriaus dydis yra skaitinė vektoriaus reikšmė ir ji apibrėžia vektoriaus ilgį. Bet kurio vektoriaus A dydis vaizduojamas kaip |A|. Vektoriaus dydis apskaičiuojamas pagal formulę,

Bet kurio vektoriaus A = xi + yj + zk jo dydis nustatomas pagal formulę

|A| = √(x ² + ir ² + z ² )

Bet kuriam vektoriui, kurio pradžios ir pabaigos taškai yra atitinkamai (x₁, ir₁) ir (x₂, ir₂) jo dydis pateikiamas formule

|A| = √((x ₂ – x ₁ ) ² + (ir ₂ - ir ₁ ) ² )

Kaip pavaizduoti vektoriaus dydį?

Vektoriaus dydis A yra pavaizduotas simboliu |A|.

Kaip rasti vektoriaus dydį?

Vektoriaus dydžiui apskaičiuoti naudojamos įvairios formulės, kai kurios iš jų yra,

|A| = √(x ² + ir ² + z ² ) kai vektorius yra A = xi + yj + zk formos
|A| = √((x) ² + (ir) ² ) kai vektorius duotas tašku A (x, y) ir pradine O(0, 0).
|A| = √((x ₂ – x ₁ ) ² + (ir ₂ - ir ₁ ) ² ) kai vektorius pateikiamas tašku A (x₁, ir₂) ir tašką B (x₂, ir₂).

Raskite 5 dydžio vektorių.

Yra įvairių vektorių, kurių dydis gali būti 5, pavyzdžiui, vektorius A vaizduojamas kaip

A = 3i + 4j arba A = 4i + 5j