Logistinė regresija yra prižiūrimas mašininio mokymosi algoritmas naudojama klasifikavimo užduotys kur tikslas yra numatyti tikimybę, kad egzempliorius priklauso tam tikrai klasei, ar ne. Logistinė regresija yra statistinis algoritmas, analizuojantis ryšį tarp dviejų duomenų veiksnių. Straipsnyje nagrinėjami logistinės regresijos pagrindai, jos rūšys ir įgyvendinimas.

Turinys

• Kas yra logistinė regresija?
• Logistinė funkcija – Sigmoidinė funkcija
• Logistinės regresijos rūšys
• Logistinės regresijos prielaidos
• Kaip veikia logistinė regresija?
• Logistinės regresijos kodo įgyvendinimas
• Tikslumo ir atšaukimo kompromisas logistinės regresijos slenksčio nustatyme
• Kaip įvertinti logistinės regresijos modelį?
• Linijinės ir logistinės regresijos skirtumai

Kas yra logistinė regresija?

Logistinė regresija naudojama dvejetainei klasifikacija kur mes naudojame sigmoidinė funkcija , kuris priima įvestį kaip nepriklausomus kintamuosius ir sukuria tikimybės reikšmę nuo 0 iki 1.

Pavyzdžiui, turime dvi klases: 0 klasė ir 1 klasė, jei įvesties logistinės funkcijos reikšmė yra didesnė nei 0,5 (slenkstinė reikšmė), tada ji priklauso 1 klasei, kitaip ji priklauso 0 klasei. Tai vadinama regresija, nes ji yra pratęsimas tiesinė regresija bet daugiausia naudojamas klasifikavimo problemoms spręsti.

Pagrindiniai klausimai:

• Logistinė regresija numato kategoriškai priklausomo kintamojo išvestį. Todėl rezultatas turi būti kategoriška arba atskira reikšmė.
• Tai gali būti Taip arba Ne, 0 arba 1, tiesa arba klaidinga ir tt, tačiau vietoj tikslios reikšmės 0 ir 1 pateikiamos tikimybinės reikšmės, kurios yra nuo 0 iki 1.
• Logistinėje regresijoje vietoj regresijos tiesės pritaikymo pritaikome S formos logistinę funkciją, kuri numato dvi didžiausias reikšmes (0 arba 1).

Logistinė funkcija – Sigmoidinė funkcija

• Sigmoidinė funkcija yra matematinė funkcija, naudojama numatomoms reikšmėms susieti su tikimybėmis.
• Jis susieja bet kokią realią reikšmę į kitą vertę, esančią nuo 0 iki 1. Logistinės regresijos reikšmė turi būti nuo 0 iki 1, kuri negali viršyti šios ribos, todėl sudaro kreivę, panašią į S formą.
• S formos kreivė vadinama sigmoidine funkcija arba logistine funkcija.
• Logistinės regresijos metu naudojame slenkstinės reikšmės sąvoką, kuri apibrėžia 0 arba 1 tikimybę. Pavyzdžiui, vertės, viršijančios slenkstinę vertę, linkusios į 1, o mažesnės už slenksčius – į 0.

Logistinės regresijos rūšys

Pagal kategorijas logistinę regresiją galima suskirstyti į tris tipus:

1. Dvejetainė: Taikant dvinarę logistinę regresiją, gali būti tik du priklausomų kintamųjų tipai, pvz., 0 arba 1, patvirtinta arba nepavyko ir kt.
2. Daugiavardis: Daugianomėje logistinėje regresijoje gali būti 3 ar daugiau galimų nerūšiuotų priklausomo kintamojo tipų, tokių kaip katė, šunys arba avys.
3. Eilinis: Eilinėje logistinėje regresijoje gali būti 3 ar daugiau galimų sutvarkytų tipų priklausomų kintamųjų, tokių kaip žemas, vidutinis arba aukštas.

Logistinės regresijos prielaidos

Išnagrinėsime logistinės regresijos prielaidas, nes suprasti šias prielaidas svarbu užtikrinti, kad mes naudojame tinkamą modelio taikymą. Prielaida apima:

1. Nepriklausomi stebėjimai: kiekvienas stebėjimas yra nepriklausomas nuo kito. reiškia, kad nėra jokios koreliacijos tarp jokių įvesties kintamųjų.
2. Dvejetainiai priklausomi kintamieji: daroma prielaida, kad priklausomasis kintamasis turi būti dvejetainis arba dichotominis, tai reiškia, kad jis gali turėti tik dvi reikšmes. Daugiau nei dviem kategorijoms naudojamos SoftMax funkcijos.
3. Tiesiškumo ryšys tarp nepriklausomų kintamųjų ir loginių šansų: ryšys tarp nepriklausomų kintamųjų ir priklausomo kintamojo loginio koeficiento turėtų būti tiesinis.
4. Jokių nuokrypių: duomenų rinkinyje neturėtų būti jokių nukrypimų.
5. Didelis imties dydis: imties dydis yra pakankamai didelis

Logistinės regresijos terminijos

Štai keletas bendrų terminų, susijusių su logistine regresija:

• Nepriklausomi kintamieji: Įvesties charakteristikos arba numatymo veiksniai, taikomi priklausomo kintamojo prognozėms.
• Priklausomas kintamasis: Tikslinis logistinės regresijos modelio kintamasis, kurį bandome numatyti.
• Logistinė funkcija: Formulė, naudojama parodyti, kaip nepriklausomi ir priklausomi kintamieji yra susiję vienas su kitu. Logistinė funkcija paverčia įvesties kintamuosius į tikimybės reikšmę nuo 0 iki 1, kuri parodo tikimybę, kad priklausomas kintamasis yra 1 arba 0.
• Šansai: Tai yra kažkas vykstančio ir neįvykusio santykis. ji skiriasi nuo tikimybės, nes tikimybė yra santykis, kad kažkas atsitiks ir viskas, kas gali įvykti.
• Log-odds: Log-odds, taip pat žinomas kaip logit funkcija, yra natūralus koeficientų logaritmas. Logistinėje regresijoje priklausomo kintamojo loginiai šansai modeliuojami kaip tiesinis nepriklausomų kintamųjų ir pertraukos derinys.
• Koeficientas: Logistinės regresijos modelio įvertinti parametrai parodo, kaip nepriklausomi ir priklausomi kintamieji yra susiję vienas su kitu.
• Perimti: Logistinės regresijos modelio pastovus terminas, nurodantis loginį koeficientą, kai visi nepriklausomi kintamieji yra lygūs nuliui.
• Didžiausios tikimybės įvertinimas : Logistinės regresijos modelio koeficientams įvertinti naudojamas metodas, kuris maksimaliai padidina modelio duomenų stebėjimo tikimybę.

Kaip veikia logistinė regresija?

Logistinės regresijos modelis transformuoja tiesinė regresija funkcija nuolatinės vertės išvestis į kategorinės vertės išvestį naudojant sigmoidinę funkciją, kuri bet kurią realios vertės nepriklausomų kintamųjų rinkinį atvaizduoja į reikšmę nuo 0 iki 1. Ši funkcija vadinama logistine funkcija.

Tegul nepriklausomos įvesties funkcijos yra:

X = egin{bmatrix} x_{11} & … & x_{1m} x_{21} & … & x_{2m} vdots & ddots & vdots x_{n1} & … & x_{nm} end{bmatrix}

šaukštelio dydžio

ir priklausomas kintamasis yra Y, turintis tik dvejetainę reikšmę, ty 0 arba 1.

Y = egin{cases} 0 & ext{ if } Class;1 1 & ext{ if } Class;2 end{cases}

tada taikykite daugiatiesę funkciją įvesties kintamiesiems X.

z = left(sum_{i=1}^{n} w_{i}x_{i} ight) + b

čiax_i yra i-asis X stebėjimas,w_i = [w_1, w_2, w_3, cdots,w_m] yra svoriai arba koeficientas, o b yra poslinkio terminas, dar žinomas kaip pertrauka. tiesiog tai gali būti pavaizduota kaip svorio ir šališkumo taškinė sandauga.

z = wcdot X +b

kad ir ką aptarėme aukščiau, yra tiesinė regresija .

Sigmoidinė funkcija

Dabar mes naudojame sigmoidinė funkcija kur įvestis bus z ir randame tikimybę tarp 0 ir 1. t.y. prognozuojamas y.

sigma(z) = frac{1}{1-e^{-z}}

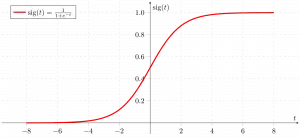
Sigmoidinė funkcija

Kaip parodyta aukščiau, figūrinė sigmoidinė funkcija konvertuoja nuolatinius kintamuosius duomenis į tikimybė t.y. nuo 0 iki 1.

• sigma(z) linkęs į 1 asz ightarrowinfty
• sigma(z) linkęs į 0 asz ightarrow-infty
• sigma(z) visada ribojamas nuo 0 iki 1

kur tikimybę būti klase galima išmatuoti taip:

P(y=1) = sigma(z) P(y=0) = 1-sigma(z)

Logistinės regresijos lygtis

Nelyginis yra santykis, kai kažkas įvyksta ir kažkas neįvyksta. ji skiriasi nuo tikimybės, nes tikimybė yra santykis, kad kažkas atsitiks ir viskas, kas gali įvykti. taip keista bus:

frac{p(x)}{1-p(x)} = e^z

kampinė medžiaga

Natūralaus rąsto taikymas ant nelyginio. tada log nelyginis bus:

egin{aligned} log left[frac{p(x)}{1-p(x)} ight] &= z log left[frac{p(x)}{1-p(x)} ight] &= wcdot X +b frac{p(x)}{1-p(x)}&= e^{wcdot X +b} ;;cdots ext{Exponentiate both sides} p(x) &=e^{wcdot X +b}cdot (1-p(x)) p(x) &=e^{wcdot X +b}-e^{wcdot X +b}cdot p(x)) p(x)+e^{wcdot X +b}cdot p(x))&=e^{wcdot X +b} p(x)(1+e^{wcdot X +b}) &=e^{wcdot X +b} p(x)&= frac{e^{wcdot X +b}}{1+e^{wcdot X +b}} end{aligned}

tada galutinė logistinės regresijos lygtis bus tokia:

p(X;b,w) = frac{e^{wcdot X +b}}{1+e^{wcdot X +b}} = frac{1}{1+e^{-wcdot X +b}}

Logistinės regresijos tikimybės funkcija

Numatomos tikimybės bus tokios:

• jei y=1 Numatytos tikimybės bus tokios: p(X;b,w) = p(x)
• jei y = 0 Numatomos tikimybės bus tokios: 1-p(X;b,w) = 1-p(x)

L(b,w) = prod_{i=1}^{n}p(x_i)^{y_i}(1-p(x_i))^{1-y_i}

sąrašo mazgas java

Natūralių rąstų paėmimas iš abiejų pusių

egin{aligned}log(L(b,w)) &= sum_{i=1}^{n} y_ilog p(x_i);+; (1-y_i)log(1-p(x_i)) &=sum_{i=1}^{n} y_ilog p(x_i)+log(1-p(x_i))-y_ilog(1-p(x_i)) &=sum_{i=1}^{n} log(1-p(x_i)) +sum_{i=1}^{n}y_ilog frac{p(x_i)}{1-p(x_i} &=sum_{i=1}^{n} -log1-e^{-(wcdot x_i+b)} +sum_{i=1}^{n}y_i (wcdot x_i +b) &=sum_{i=1}^{n} -log1+e^{wcdot x_i+b} +sum_{i=1}^{n}y_i (wcdot x_i +b) end{aligned}

Log-likelihood funkcijos gradientas

Norėdami rasti didžiausios tikimybės įverčius, atskiriame w.r.t w,

egin{aligned} frac{partial J(l(b,w)}{partial w_j}&=-sum_{i=n}^{n}frac{1}{1+e^{wcdot x_i+b}}e^{wcdot x_i+b} x_{ij} +sum_{i=1}^{n}y_{i}x_{ij} &=-sum_{i=n}^{n}p(x_i;b,w)x_{ij}+sum_{i=1}^{n}y_{i}x_{ij} &=sum_{i=n}^{n}(y_i -p(x_i;b,w))x_{ij} end{aligned}

Logistinės regresijos kodo įgyvendinimas

Binominė logistinė regresija:

Tikslinis kintamasis gali turėti tik 2 galimus tipus: 0 arba 1, kurie gali reikšti laimėjimą prieš pralaimėjimą, pralaimėjimą prieš nesėkmę, mirusį prieš gyvą ir pan., šiuo atveju naudojamos sigmoidinės funkcijos, apie kurias jau buvo kalbama aukščiau.

Reikiamų bibliotekų importavimas pagal modelio reikalavimą. Šis „Python“ kodas parodo, kaip naudoti krūties vėžio duomenų rinkinį, kad būtų galima įdiegti logistinės regresijos modelį klasifikavimui.

Išvestis :

Logistinės regresijos modelio tikslumas (%): 95.6140350877193

Daugianomė logistinė regresija:

Tikslinis kintamasis gali turėti 3 ar daugiau galimų tipų, kurie nėra išdėstyti (t. y. tipai neturi kiekybinės reikšmės), pvz., liga A, liga B ir liga C.

Šiuo atveju vietoje sigmoidinės funkcijos naudojama softmax funkcija. Softmax funkcija K klasėms bus:

ext{softmax}(z_i) =frac{ e^{z_i}}{sum_{j=1}^{K}e^{z_{j}}}

Čia K reiškia elementų skaičių vektoriuje z, o i, j kartojasi per visus vektoriaus elementus.

Tada c klasės tikimybė bus tokia:

P(Y=c | overrightarrow{X}=x) = frac{e^{w_c cdot x + b_c}}{sum_{k=1}^{K}e^{w_k cdot x + b_k}}

Daugianominėje logistinėje regresijoje išvesties kintamasis gali turėti daugiau nei du galimi atskiri išėjimai . Apsvarstykite skaitmeninių duomenų rinkinį.

Išvestis:

Logistinės regresijos modelio tikslumas (%): 96.52294853963839

Kaip įvertinti logistinės regresijos modelį?

Logistinės regresijos modelį galime įvertinti naudodami šiuos rodiklius:

• Tikslumas: Tikslumas pateikia teisingai klasifikuotų atvejų proporciją.
  Accuracy = frac{True , Positives + True , Negatives}{Total}

• Tikslumas: Tikslumas daugiausia dėmesio skiria teigiamų prognozių tikslumui.
  Precision = frac{True , Positives }{True, Positives + False , Positives}

• Atšaukimas (jautrumas arba tikras teigiamas rodiklis): Prisiminkite matuoja teisingai numatytų teigiamų atvejų dalį tarp visų faktinių teigiamų atvejų.
  Recall = frac{ True , Positives}{True, Positives + False , Negatives}

• F1 rezultatas: F1 rezultatas yra harmoningas tikslumo ir prisiminimo vidurkis.
  F1 , Score = 2 * frac{Precision * Recall}{Precision + Recall}

• Plotas po imtuvo veikimo charakteristikų kreive (AUC-ROC): ROC kreivė vaizduoja tikrąjį teigiamą rodiklį ir klaidingai teigiamą dažnį esant įvairioms slenksčiams. AUC-ROC matuoja plotą po šia kreive, suteikdamas bendrą modelio našumo matą skirtingose ​​klasifikacijos ribose.
• Plotas po tikslumo atšaukimo kreive (AUC-PR): Panašus į AUC-ROC, AUC-PR matuoja plotą po tikslumo atšaukimo kreive, pateikdamas modelio veikimo santrauką atsižvelgiant į skirtingus tikslumo atšaukimo kompromisus.

Tikslumo ir atšaukimo kompromisas logistinės regresijos slenksčio nustatyme

Logistinė regresija tampa klasifikavimo technika tik tada, kai į paveikslą įtraukiamas sprendimo slenkstis. Slenkstinės reikšmės nustatymas yra labai svarbus logistinės regresijos aspektas ir priklauso nuo pačios klasifikavimo problemos.

Sprendimą dėl slenkstinės vertės didžiausios įtakos turi reikšmės tikslumas ir prisiminimas. Idealiu atveju norime ir tikslumo, ir prisiminimo, kad būtų 1, tačiau taip būna retai.

Tuo atveju, kai a Precision-Recall kompromisas , mes naudojame šiuos argumentus, kad nuspręstume dėl slenksčio:

1. Žemas tikslumas / didelis atšaukimas: Programose, kuriose norime sumažinti klaidingų neigiamų skaičių, nebūtinai sumažindami klaidingų teigiamų rezultatų skaičių, pasirenkame sprendimo reikšmę, kurios tikslumo reikšmė yra maža arba Recall reikšmė didelė. Pavyzdžiui, vėžio diagnozavimo programoje nenorime, kad bet kuris paveiktas pacientas būtų klasifikuojamas kaip nepažeistas, nekreipiant dėmesio į tai, ar pacientui neteisingai diagnozuotas vėžys. Taip yra todėl, kad vėžio nebuvimą galima aptikti kitomis medicininėmis ligomis, tačiau jau atmestam kandidatui ligos aptikti negalima.
2. Didelis tikslumas / mažas atšaukimas: Programose, kuriose norime sumažinti klaidingų teigiamų rezultatų skaičių, nebūtinai sumažindami klaidingų neigiamų skaičių, pasirenkame sprendimo reikšmę, kuri turi didelę Tikslumo reikšmę arba mažą atšaukimo reikšmę. Pavyzdžiui, klasifikuodami klientus, ar jie teigiamai ar neigiamai reaguos į suasmenintą reklamą, norime būti visiškai tikri, kad klientas į reklamą reaguos teigiamai, nes priešingu atveju neigiama reakcija gali prarasti potencialius pardavimus iš klientas.

Linijinės ir logistinės regresijos skirtumai

Skirtumas tarp tiesinės regresijos ir logistinės regresijos yra tas, kad tiesinės regresijos išvestis yra nuolatinė vertė, kuri gali būti bet kokia, o logistinė regresija numato tikimybę, kad egzempliorius priklauso tam tikrai klasei, ar ne.

kitas skaitytuvas

Logistinė regresija – dažnai užduodami klausimai (DUK)

Kas yra mašininio mokymosi logistinė regresija?

Logistinė regresija yra statistinis mašininio mokymosi modelių su dvejetainiais priklausomais kintamaisiais, ty dvejetainiais, kūrimo metodas. Logistinė regresija yra statistinis metodas, naudojamas apibūdinti duomenis ir ryšį tarp vieno priklausomo kintamojo ir vieno ar daugiau nepriklausomų kintamųjų.

Kokie yra trys logistinės regresijos tipai?

Logistinė regresija skirstoma į tris tipus: dvejetainę, daugianarę ir eilinę. Jie skiriasi vykdymu ir teorija. Dvejetainė regresija yra susijusi su dviem galimais rezultatais: taip arba ne. Daugianomė logistinė regresija naudojama, kai yra trys ar daugiau reikšmių.

Kodėl klasifikavimo problemai naudojama logistinė regresija?

Logistinę regresiją lengviau įgyvendinti, interpretuoti ir mokyti. Ji labai greitai klasifikuoja nežinomus įrašus. Kai duomenų rinkinys yra tiesiškai atskiriamas, jis veikia gerai. Modelio koeficientai gali būti interpretuojami kaip požymio svarbos rodikliai.

Kuo logistinė regresija skiriasi nuo tiesinės regresijos?

Linijinė regresija naudojama nenutrūkstamiems rezultatams prognozuoti, o logistinė regresija naudojama tikimybei, kad stebėjimas pateks į konkrečią kategoriją, numatyti. Logistinė regresija naudoja S formos logistinę funkciją, kad būtų galima nustatyti numatomas reikšmes nuo 0 iki 1.

Kokį vaidmenį logistinėje regresijoje atlieka logistinė funkcija?

Logistinė regresija remiasi logistine funkcija, kad konvertuotų išvestį į tikimybės balą. Šis balas parodo tikimybę, kad stebėjimas priklauso tam tikrai klasei. S formos kreivė padeda nustatyti slenkstį ir suskirstyti duomenis į dvejetainius rezultatus.