Linijinis programavimas yra matematinė sąvoka, naudojama ieškant optimalaus tiesinės funkcijos sprendimo. Šis metodas naudoja paprastas prielaidas, skirtas optimizuoti pateiktą funkciją. Linijinis programavimas turi didžiulę realaus pasaulio programą ir yra naudojamas įvairių tipų problemoms spręsti.
Linijinis programavimas naudojamas įvairiose pramonės šakose, tokiose kaip laivybos pramonė, gamybos pramonė, transporto pramonė, telekomunikacijos ir kt.
Terminas „linijinis programavimas“ susideda iš dviejų žodžių „linijinis“ ir „programavimas“, žodis „linijinis“ nurodo ryšį tarp įvairių tipų vieno laipsnio kintamųjų, naudojamų užduotyje, o žodis „programavimas“ nurodo žingsnis po žingsnio šių problemų sprendimo procedūrą.
Šiame straipsnyje mes išsamiai sužinosime apie tiesinį programavimą, jo pavyzdžius, formules ir kitas sąvokas.
Turinys
- Kas yra linijinis programavimas?
- Linijinio programavimo komponentai
- Linijinio programavimo pavyzdžiai
- Linijinio programavimo problemos
- Linijinio programavimo problemų tipai
- Linijinio programavimo formulė
- Kaip išspręsti linijinio programavimo problemas?
- Linijinio programavimo metodai
- Linijinio programavimo paprastasis metodas
- Linijinio programavimo grafinis metodas
- Linijinio programavimo programos
- Linijinio programavimo svarba
- Naujausios linijinio programavimo programos
- Linijinis programavimas operacijų tyrime
- Paprastasis metodas
Kas yra linijinis programavimas?
Linijinis programavimas arba Linijinis optimizavimas yra technika, kuri padeda mums rasti optimalų tam tikros problemos sprendimą, optimalus sprendimas yra sprendimas, kuris yra geriausias galimas konkrečios problemos rezultatas.
Paprastais žodžiais tariant, tai yra būdas išsiaiškinti, kaip ką nors padaryti geriausiu įmanomu būdu. Turėdami ribotus išteklius, turite optimaliai panaudoti išteklius ir pasiekti geriausią įmanomą rezultatą, siekdami konkretaus tikslo, pvz., mažiausią kainą, didžiausią maržą ar trumpiausią laiką.
Situacija, kai reikia ieškoti geriausių kintamųjų, kuriems taikomi tam tikri apribojimai, reikšmių, yra tada, kai naudojame linijinio programavimo problemas. Šių situacijų negalima išspręsti naudojant įprastus skaičiavimo ir skaitmeninius metodus.
Linijinio programavimo apibrėžimas
Linijinis programavimas yra metodas, naudojamas tam tikram scenarijui optimizuoti. Linijinio programavimo naudojimas suteikia mums geriausią įmanomą rezultatą tam tikroje situacijoje. Jis naudoja visus turimus išteklius taip, kad pasiektų optimalų rezultatą.
Linijinio programavimo komponentai
Pagrindiniai linijinio programavimo (LP) problemos komponentai yra šie:
- Sprendimo kintamieji: Kintamieji, kuriuos norite nustatyti, kad pasiektumėte optimalų sprendimą.
- Tikslinė funkcija: M atematinė lygtis, nurodanti tikslą, kurį norite pasiekti
- Apribojimai: Apribojimai arba apribojimai, kurių turi laikytis jūsų sprendimo kintamieji.
- Ne neigiamumo apribojimai: Kai kuriose realaus pasaulio scenarijus, sprendimų kintamieji negali būti neigiami
Papildomos linijinio programavimo charakteristikos
- Baigtumas: Sprendimo kintamųjų ir apribojimų skaičius LP uždavinyje yra baigtinis.
- Tiesiškumas: Tikslinė funkcija ir visi apribojimai turi būti tiesinės sprendimo kintamųjų funkcijos . Tai reiškia, kad kintamųjų laipsnis turi būti vienas.
Linijinio programavimo pavyzdžiai
Situacijas, kuriose taikomas linijinis programavimas, galime suprasti naudodami toliau aptartą pavyzdį,
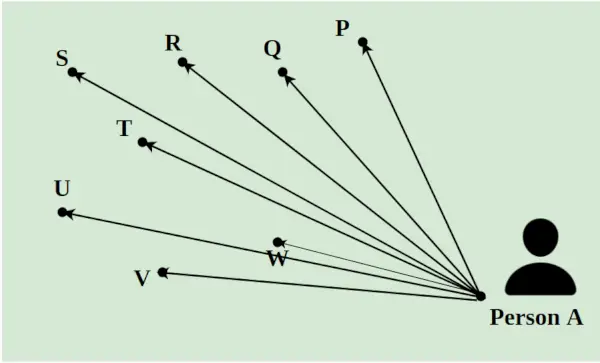
Tarkime, siuntėjas turi pristatyti 8 paketus per dieną į skirtingas miesto vietas. Jis turi pasirinkti visus paketus iš A ir pristatyti juos į taškus P, Q, R, S, T, U, V ir W. Atstumas tarp jų nurodomas linijomis, kaip parodyta paveikslėlyje žemiau. Trumpiausias kelias, kuriuo eina pristatymo žmogus, apskaičiuojamas naudojant linijinio programavimo koncepciją.
Python yra skaitinis
Linijinio programavimo problemos
Linijinio programavimo problemos (LPP) apima tiesinės funkcijos optimizavimą, kad būtų galima rasti optimalų funkcijos vertės sprendimą. Optimali vertė gali būti didžiausia arba mažiausia.
LPP linijinės funkcijos vadinamos objektyvios funkcijos. Tikslinė funkcija gali turėti kelis kintamuosius, kuriems taikomos sąlygos ir kurie turi atitikti linijiniai apribojimai .
Linijinio programavimo problemų tipai
Yra daug skirtingų linijinio programavimo problemų (LPP), tačiau šiame straipsnyje aptarsime tris pagrindines linijinio programavimo problemas.
Gamybos problemos
Gamybos problemos yra problema, susijusi su vienetų, kurie turėtų būti pagaminti arba parduoti, kad būtų padidintas pelnas, skaičiumi, kai kiekvienam gaminiui reikia fiksuotos darbo jėgos, mašinų valandų ir žaliavų.
Dietos problemos
Jis naudojamas apskaičiuojant įvairių rūšių sudedamųjų dalių, kurios turi būti įtrauktos į dietą, skaičių, kad būtų gauta mažiausia kaina, atsižvelgiant į maisto prieinamumą ir jų kainas.
Transporto problemos
Jis naudojamas transportavimo tvarkaraščiui nustatyti, siekiant rasti pigiausią būdą transportuoti produktą iš gamyklų / gamyklų, esančių skirtingose vietose, į skirtingas rinkas.
Linijinio programavimo formulė
Linijinio programavimo uždavinys susideda iš:
- Sprendimo kintamieji
- Objektyvi funkcija
- Apribojimai
- Neneigiami apribojimai
Sprendimo kintamieji yra kintamieji x ir y, kurie lemia tiesinio programavimo uždavinio išvestį ir pateikia galutinį sprendimą.
The objektyvi funkcija , paprastai pavaizduotas Z, yra tiesinė funkcija, kurią reikia optimizuoti pagal pateiktą sąlygą, kad būtų gautas galutinis sprendimas.
The apribojimai primesti sprendimų kintamiesiems, ribojantiems jų reikšmes, vadinami apribojimais.
Dabar bendroji linijinio programavimo uždavinio formulė yra
Objektyvi funkcija : Z = kirvis + by
Apribojimai: cx + dy ≥ e, px + qy ≤ r
Neneigiami apribojimai: x ≥ 0, y ≥ 0
Aukščiau pateiktose sąlygose x ir y yra sprendimo kintamieji.
Kaip išspręsti linijinio programavimo problemas?
Prieš sprendžiant linijinio programavimo uždavinius, pirmiausia turime suformuluoti uždavinius pagal standartinius parametrus. Tiesinio programavimo problemų sprendimo žingsniai yra šie:
1 žingsnis: Užduotyje pažymėkite sprendimo kintamuosius.
2 žingsnis: Sukurkite tikslią problemos funkciją ir patikrinkite, ar funkciją reikia sumažinti ar padidinti.
3 veiksmas: Užrašykite visus tiesinių uždavinių apribojimus.
4 veiksmas: Užtikrinti neneigiamus sprendimo kintamųjų apribojimus.
5 veiksmas: Dabar išspręskite linijinio programavimo problemą naudodami bet kurį metodą, paprastai mes naudojame simpleksinį arba grafinį metodą.
Linijinio programavimo metodai
Linijinio programavimo uždaviniams spręsti naudojame įvairius metodus. Du dažniausiai naudojami metodai yra
- Paprastasis metodas
- Grafinis metodas
Išsamiai sužinokime apie šiuos du metodus šiame straipsnyje,
Linijinio programavimo paprastasis metodas
Vienas iš labiausiai paplitusių linijinio programavimo uždavinių sprendimo būdų yra simpleksinis metodas. Taikant šį metodą, tam tikrą sąlygą „n“ kartojame keletą kartų, kol pasiekiamas optimalus sprendimas.
Veiksmai, reikalingi linijinio programavimo problemoms išspręsti naudojant simplekso metodą:
1 žingsnis: Suformuluokite linijinio programavimo uždavinius pagal pateiktus apribojimus.
2 žingsnis: Konvertuokite visas nurodytas nelygybes į linijinio programavimo uždavinių lygtis arba lygybes, pridedant laisvąjį kintamąjį prie kiekvienos nelygybės, kur kada reikia.
3 veiksmas: Sukurkite pradinę simplekso lentelę. Pateikdami kiekvieną apribojimo lygtį iš eilės ir parašydami tikslo funkciją apatinėje eilutėje. Taip gauta lentelė vadinama Simplex lentele.
4 veiksmas: Nurodykite didžiausią neigiamą įrašą apatinėje eilutėje, elemento su didžiausiu neigiamu įrašu stulpelis vadinamas sukimo stulpeliu
5 veiksmas: Padalinkite dešiniojo stulpelio įrašus su atitinkamo sukimosi stulpelio įrašais, neįskaitant apatinės eilutės įrašų. Dabar eilutė, kurioje yra mažiausiai įrašo, vadinama sukimo eilute. Sukamasis elementas gaunamas susikirtimo eilutės ir sukimosi stulpelio sankirtoje.
6 veiksmas: Naudodami matricos operaciją ir sukamojo elemento pagalba padarykite, kad visi suvestinės stulpelio įrašai būtų lygūs nuliui.
7 veiksmas: Patikrinkite, ar apatinėje eilutėje nėra neigiamų įrašų, jei apatinėje eilutėje nėra neigiamų įrašų, užbaikite procesą arba pradėkite procesą iš naujo nuo 4 veiksmo.
8 veiksmas: Taip gauta galutinė simplekso lentelė pateikia mūsų problemos sprendimą.
Linijinio programavimo grafinis metodas
Grafinis metodas yra kitas metodas nei Simplex metodas, naudojamas linijinio programavimo problemoms spręsti. Kaip rodo pavadinimas, šis metodas naudoja grafikus nurodytoms linijinio programavimo problemoms išspręsti. Tai geriausias būdas išspręsti linijinio programavimo problemas ir reikalauja mažiau pastangų nei vienpusis metodas.
Naudodami šį metodą, mes nubraižome visas nelygybes, kurioms taikomi apribojimai pateiktose linijinio programavimo uždaviniuose. Kai tik visos duotosios LPP nelygybės nubraižomos XY grafike, bendra visų nelygybių sritis duoda optimalų sprendimą. Apskaičiuojami visi galimo regiono kampiniai taškai ir visuose tuose taškuose apskaičiuojama tikslo funkcijos reikšmė, tada palyginus šias reikšmes gauname optimalų LPP sprendimą.
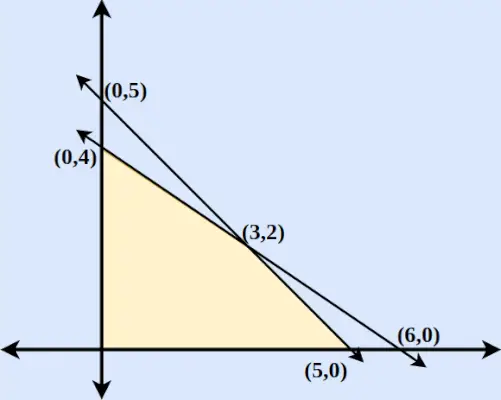
Pavyzdys: Raskite maksimalią ir mažiausią z = 6x + 9y reikšmę, kai apribojimo sąlygos yra
- 2x + 3y ≤ 12
- x ir y ≥ 0
- x + y ≤ 5
Sprendimas:
1 žingsnis : Pirmiausia konvertuokite lygtis į normaliąsias lygtis. Taigi lygtys bus 2x+3y = 0, x = 0, y = 0 ir x + y = 5.
2 žingsnis : Raskite taškus, kuriuose 2x + 3y ir x + y = 5 nupjauna x ir y ašis. Norėdami rasti x ašies susikirtimo tašką, į atitinkamą lygtį įdėkite y = 0 ir raskite tašką. Panašiai y ašies susikirtimo taškams atitinkamoje lygtyje įdėkite x = 0.
3 veiksmas : nubrėžkite dvi linijas, pjaunančias x ir y ašis. Pastebime, kad abi ašys pjauna viena kitą taške (3,2).
4 veiksmas : Jei x ≥ 0 ir y ≥ 0, nustatome, kad laikomasi abiejų nelygybių. Taigi regionas apims ploto regioną, aptvertą dviem ašimis ir abiem linijomis, įskaitant pradžią. Nubraižytas regionas parodytas žemiau esančiame paveikslėlyje.
5 veiksmas : Raskite Z kiekvienam taškui ir maksimumus bei minimumus.
Koordinatės Z = 6x + 9m (0,5) Z = 45 (0,4) Z = 36 (5,0) Z = 30 (6,0) Z = 36 (3.2) Z = 36 Taigi, mes nustatome, kad Z = 6x + 9y yra didžiausias ties (0,5), o minimalus (5,0).
Linijinio programavimo programos
Linijinis programavimas turi programų įvairiose srityse. Jis naudojamas norint nustatyti minimalias proceso išlaidas, kai pateikiami visi problemų suvaržymai. Jis naudojamas transporto priemonės transportavimo sąnaudoms optimizuoti ir pan. Įvairios linijinio programavimo programos
Inžinerinės pramonės šakos
Engineering Industries naudoja linijinį programavimą, kad išspręstų projektavimo ir gamybos problemas ir gautų maksimalią našumą esant tam tikroms sąlygoms.
Gamybos pramonės šakos
Gamybos pramonė naudoja linijinį programavimą, kad padidintų įmonių pelną ir sumažintų gamybos sąnaudas.
Energetikos pramonė
Energetikos įmonės naudoja linijinį programavimą, kad optimizuotų savo gamybos našumą.
Transporto pramonės šakos
Linijinis programavimas taip pat naudojamas transporto pramonėje, siekiant rasti būdą, kaip sumažinti transportavimo išlaidas.
Linijinio programavimo svarba
Linijinis programavimas turi didžiulę reikšmę įvairiose pramonės šakose, nes jis maksimaliai padidina išvesties vertę ir sumažina įvesties reikšmes pagal įvairius apribojimus.
LP yra labai tinkamas, kai sprendžiant problemą turime kelias sąlygas ir turime optimizuoti problemos išvestį, t. y. turime rasti mažiausią arba didžiausią reikšmę pagal tam tikrą sąlygą.
Skaityti daugiau,
- Tiesinės nelygybės
- Algebrinis tiesinių nelygybių sprendimas
Linijinio programavimo problemos
1 problema: Įmonė gamina ir parduoda dviejų rūšių gaminius, o kiekvieno a ir b vieneto gamybos savikaina yra atitinkamai 200 ir 150 rupijų, kiekvienas produkto vienetas duoda 20 rupijų pelną, o kiekvienas gaminio b vienetas duoda 15 rupijų pardavus. . Bendrovė apskaičiavo, kad A ir B mėnesio poreikis yra didžiausias nuimto vieneto kiekis visame mėnesio gamybos biudžete, nustatytas 50 000 rupijų. Kiek vienetų įmonė turėtų pagaminti, kad uždirbtų didžiausią pelną iš mėnesinių pardavimų iš ir b?
Sprendimas:
Tegu x = A tipo vienetų skaičius
y = B tipo vienetų skaičius
Padidinti Z = 40x + 50m
Atsižvelgiant į apribojimus
3x + y ≤ 9
x + 2y ≤ 8
ir x, y ≥ 0
Apsvarstykite lygtį,
3x + y = 9
x = 3
y = 0
ir x + 2y = 8
x = 8
y = 0
Dabar mes galime nustatyti didžiausią Z reikšmę įvertinę Z reikšmę keturiuose taškuose (viršūnėse), parodytuose žemiau
Viršūnės
Z = 40x + 50m
(0, 0)
Z = 40 × 0 + 50 × 0 = Rs. 0
(3, 0)
Z = 40 × 3 + 50 × 0 = Rs. 120
(0, 4)
Z = 40 × 0 + 50 × 4 = Rs. 200
(23)
Z = 40 × 2 + 50 × 3 = Rs. 230
Maksimalus pelnas, Z = Rs. 230
∴ A tipo vienetų skaičius yra 2, o B tipo vienetų skaičius yra 3.
2 problema: padidinkite Z = 3x + 4y.
Atsižvelgiant į apribojimus , x + y ≤ 450, 2x + y ≤ 600 ir x, y ≤ 0.
Sprendimas:
Turime iš duotosios
Apribojimai (1)
X + Y = 450
Įdėjus x = 0, ⇒ 0 + y = 450 ⇒ y = 450
y = 0, ⇒ x + 0 = 450 ⇒ x = 450
iš, Apribojimai (2)
2x + y = 600
Įdėjus x = 0, ⇒ 0 + y = 600 ⇒ y = 600
y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300
Dabar turime taškų koordinatę Z = 3x + 4y
| Viršūnės | Z = 3x + 4m |
|---|---|
| (0, 0) | Z = 3 × 0 + 4 × 0 = 0 |
| (300, 0) | Z = 3 × 300 + 4 × 0 = 900 |
| (150, 300) | Z = 3 × 150 + 4 × 300 = 1650 |
| (0, 450) | Z = 3 × 0 + 4 × 450 = 1800 |
Todėl optimalaus sprendimo maksimumas Z = 1800, kai koordinatė x = 0 ir y = 450. Grafikas pateiktas žemiau.
skirtumas tarp tigro ir liūto

Naujausios linijinio programavimo programos
Linijinis programavimas, galinga matematinė technika, naudojamas optimizavimo problemoms spręsti įvairiose pramonės šakose. Štai keletas šiuolaikinių programų:
- Tiekimo grandinės optimizavimas : Linijinis programavimas padeda įmonėms sumažinti išlaidas ir maksimaliai padidinti tiekimo grandinių efektyvumą. Jis naudojamas siekiant nustatyti ekonomiškiausius transportavimo maršrutus, sandėlio operacijas ir atsargų valdymo strategijas.
- Energijos valdymas Energetikos sektoriuje linijinis programavimas naudojamas energijos gamybos metodų deriniui optimizuoti. Tai apima tradicinių energijos šaltinių subalansavimą su atsinaujinančiais energijos šaltiniais, siekiant sumažinti išlaidas ir poveikį aplinkai, kartu patenkinant paklausą.
- Telekomunikacijų tinklų projektavimas : linijinio programavimo pagalba kuriant efektyvius telekomunikacijų tinklus. Tai padeda paskirstyti pralaidumą, kurti tinklo išdėstymą ir optimizuoti duomenų srautą, kad būtų užtikrintas didelės spartos ryšys mažesnėmis sąnaudomis.
- Finansų planavimas : Įmonės ir finansų analitikai naudoja linijinį programavimą portfeliui optimizuoti, rizikos valdymui ir kapitalo biudžetui sudaryti. Tai padeda priimti investicinius sprendimus, kurie padidina grąžą ir sumažina riziką.
- Sveikatos priežiūros logistika : Sveikatos priežiūros srityje linijinis programavimas taikomas siekiant optimizuoti išteklių, pvz., ligoninių lovų, medicinos personalo ir įrangos, paskirstymą. Tai labai svarbu siekiant pagerinti pacientų priežiūrą, sumažinti laukimo laiką ir efektyviai valdyti išlaidas.
- Gamybos proceso optimizavimas : Linijinis programavimas naudojamas norint nustatyti optimalius kelių produktų gamybos lygius gamybos įmonėje, atsižvelgiant į tokius apribojimus kaip darbo jėga, medžiagos ir mašinos prieinamumas.
- Žemės ūkio planavimas : Ūkininkai ir žemės ūkio planuotojai naudoja linijinį programavimą, kad nuspręstų dėl pasėlių pasirinkimo, žemės naudojimo ir išteklių paskirstymo, kad padidintų derlių ir pelną, kartu tausodami išteklius.
- Oro linijų įgulos tvarkaraštis : Avialinijos taiko linijinį programavimą, kad galėtų efektyviai suplanuoti įgulas, užtikrindamos, kad skrydžiuose būtų personalas laikantis taisyklių ir sumažinant veiklos išlaidas.
Šios programos parodo linijinio programavimo universalumą ir galią sprendžiant sudėtingas optimizavimo problemas įvairiuose sektoriuose ir parodo jo svarbą šiandieniniame duomenimis pagrįstame pasaulyje.
Linijinis programavimas operacijų tyrime
- Pagrindinis įrankis : Linijinis programavimas yra pagrindinė operacijų tyrimų priemonė, skirta optimizuoti išteklius.
- Sprendimų priėmimas : padeda priimti geriausius sprendimus dėl išteklių paskirstymo, maksimalaus pelno ar išlaidų mažinimo.
- Plačios programos : Naudojamas įvairiose srityse, tokiose kaip logistika, gamyba, finansai ir sveikatos priežiūra sudėtingoms problemoms spręsti.
- Realaus pasaulio problemų modeliavimas : paverčia realaus pasaulio problemas matematiniais modeliais, kad rastų efektyviausius sprendimus.
Paprastasis metodas
- Optimizavimo algoritmas : Simplekso metodas yra galingas algoritmas, naudojamas linijiniam programavimui, siekiant rasti optimalų linijinių nelygybių sprendimą.
- Žingsnis po žingsnio metodas : jis nuolat juda geriausio sprendimo link naršydamas įmanomo regiono kraštus, apibrėžtus apribojimais.
- Efektyvumas : Žinomas dėl savo efektyvumo sprendžiant didelio masto linijinio programavimo problemas.
- Universalumas : Taikoma įvairiose srityse, pvz., dietos planavimo, tinklo srautų, gamybos planavimo ir kt., Parodantis jos universalumą.
Linijinis programavimas – DUK
Kas yra linijinis programavimas?
Linijinis programavimas yra matematinė koncepcija, naudojama tam tikros tiesinės problemos, kuri turi įvairių apribojimų, optimizavimui. Naudodami linijinį programavimą, gauname optimalų pateiktos problemos rezultatą
Kas yra linijinio programavimo problemos?
Linijinės programavimo problemos (LPP) – tai problemos, kurios pateikia optimalų tam tikrų sąlygų sprendimą.
Kas yra linijinio programavimo formulė?
Bendrosios linijinio programavimo formulės yra
- Tikslinė funkcija: Z = ax + by
- Apribojimai: px + qy ≤ r, sx + ty ≤ u
- Neneigiami apribojimai: x ≥ 0, y ≥ 0
Kokie yra skirtingi linijinio programavimo tipai?
Skirtingi linijinio programavimo metodai yra:
- Linijinis programavimas Simplex metodu
- Linijinis programavimas R metodu
- Linijinis programavimas grafiniu metodu
Kokie yra linijinio programavimo reikalavimai?
Įvairūs linijinio programavimo problemų reikalavimai yra,
- Tiesiškumas
- Objektyvi funkcija
- Apribojimai
- Ne negatyvumas
Kokie yra linijinio programavimo pranašumai?
Įvairūs linijinio programavimo pranašumai yra:
- Tai suteikia optimalų bet kurios tiesinės problemos sprendimą.
- Tai lengva naudoti ir visada duoda nuoseklius rezultatus
- Tai padeda maksimaliai padidinti pelną ir sumažinti sąnaudas.