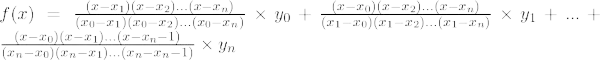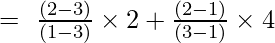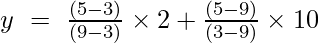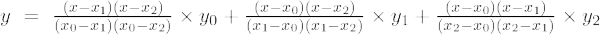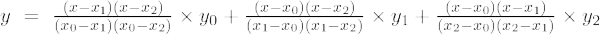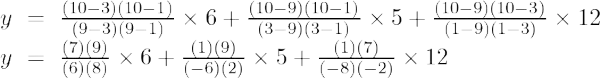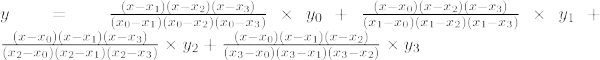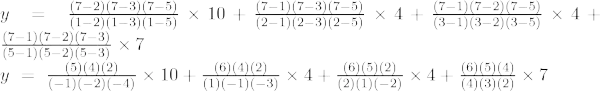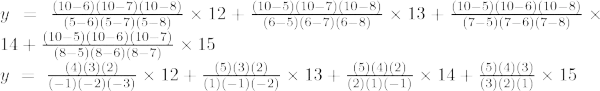logo

TechCodeview

Lagranžo interpoliacijos formulė

Lagranžo interpoliacijos formulė randa daugianarį, vadinamą Lagranžo polinomu, kuris įgauna tam tikras reikšmes savavališkame taške. Tai n-asis laipsnis funkcijos f(x) daugianario išraiška. Interpoliacijos metodas naudojamas naujiems duomenų taškams rasti žinomų duomenų taškų diskrečiųjų rinkinių diapazone.

Šiame straipsnyje mes išsamiai sužinosime apie Lagranžo interpoliaciją, Lagranžo interpoliacijos formulę, Lagranžo interpoliacijos formulės įrodymą, Lagranžo interpoliacijos formulės pavyzdžius ir kitus.



Kas yra Lagranžo interpoliacija?

Lagranžo interpoliacija yra būdas rasti bet kurios funkcijos reikšmę bet kuriame taške, kai funkcija nėra pateikta. Naudojame kitus funkcijos taškus, kad gautume funkcijos reikšmę bet kuriame reikiamame taške.

Tarkime, kad turime funkciją y = f(x), kurioje pakeitus x reikšmes gaunamos skirtingos y reikšmės. Ir mums suteikiami du taškai (x1, ir1) ir (x2, ir2) kreivėje, tada y reikšmė, kai x = a (konstanta), apskaičiuojama naudojant Lagranžo interpoliacijos formulę.

Lagranžo interpoliacijos formulė

Pateiktos kelios tikrosios reikšmės x1, x2, x3, …, xnir y1, ir2, ir3, … irnir bus daugianomas P su realiais koeficientais, atitinkančiais sąlygas P(xi) = iri, ∀ i = {1, 2, 3, …, n} ir daugianario P laipsnis turi būti mažesnis už realių verčių skaičių, t. y. laipsnį (P)



Lagranžo interpoliacijos formulė n-jai tvarkai

Lagranžo interpoliacijos formulė nthlaipsnio polinomas pateiktas žemiau:

Lagranžo interpoliacijos formulė n th tvarka yra,

f(x)=frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} imes y_0+ frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} imes y_1+...+ frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n



Lagranžo pirmosios eilės interpoliacijos formulė

Jei Polinomo laipsnis yra 1, tada jis vadinamas pirmosios eilės polinomu. Lagranžo interpoliacijos formulė 1Švpolinomų tvarka yra,

f(x)~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Lagranžo antros eilės interpoliacijos formulė

Jei daugianario laipsnis yra 2, tada jis vadinamas antros eilės polinomu. Lagranžo interpoliacijos formulė antros eilės polinomams yra,

f(x)~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)} {(x_1-x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

Lagranžo teoremos įrodymas

Panagrinėkime pateiktos formos n-ojo laipsnio daugianarį,

f(x) = A0(x – x1)(x – x2)(x – x3)…(x – xn) + A1(x – x1)(x – x2)(x – x3)…(x – xn) + … + A(n-1)(x – x1)(x – x2)(x – x3)…(x – xn)

Pakeiskite pastabas xigauti Ai

Įdėkite x = x0tada gauname A0

f(x0) = ir0= A0(x0– x1)(x0– x2)(x0– x3)…(x0– xn)

A 0 = ir 0 /(x 0 – x 1 )(x 0 – x 2 )(x 0 – x 3 )…(x 0 – x n )

Pakeičiant x = x1gauname A1

f(x1) = ir1= A1(x1– x0)(x1– x2)(x1– x3)…(x1– xn)

A 1 = ir 1 /(x 1 – x 0 )(x 1 – x 2 )(x 1 – x 3 )…(x 1 – x n )

Panašiai, pakeičiant x = xngauname An

f(xn) = irn= An(xn– x0)(xn– x1)(xn– x2)…(xn– xn-1)

A n = ir n /(x n – x 0 )(x n – x 1 )(x n – x 2 )…(x n – x n-1 )

Jei pakeisime visas A reikšmesifunkcijoje f(x), kur i = 1, 2, 3, …n, tada gauname Lagranžo interpoliacijos formulę kaip,

f(x)~=~frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} y_0+frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} imes y_1+... +frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n

Lagranžo interpoliacijos formulės savybės

Toliau aptariamos įvairios Lagranžo interpoliacijos formulės savybės,

  • Ši formulė naudojama funkcijos reikšmei rasti bet kuriame taške, net jei pati funkcija nėra pateikta.
  • Jis naudojamas net tada, kai pateikti taškai nėra tolygiai išdėstyti.
  • Jis suteikia priklausomo kintamojo reikšmę bet kuriam nepriklausomam kintamajam, priklausančiam bet kuriai funkcijai, todėl yra naudojamas skaitinėje analizėje ieškant funkcijos reikšmės ir kt.

Lagranžo interpoliacijos formulės panaudojimas

Toliau aptariami įvairūs Lagranžo interpoliacijos formulės naudojimo būdai,

  • Jis naudojamas norint rasti priklausomo kintamojo vertę bet kuriame nepriklausomame kintamajame, net jei pati funkcija nėra pateikta.
  • Jis naudojamas vaizdo mastelio keitimui.
  • Jis naudojamas AI modeliavimui.
  • Jis naudojamas mokant NLP ir kt.

Skaityti daugiau,

  • Interpoliacijos formulė
  • Tiesinės interpoliacijos formulė

Lagranžo interpoliacijos formulės naudojimo pavyzdžiai

Pažvelkime į keletą pavyzdinių klausimų apie Lagranžo interpoliacijos formulę.

1 pavyzdys: suraskite y reikšmę, kai x = 2 nurodytai taškų rinkiniui (1, 2), (3, 4)

listnode java

Sprendimas:

Atsižvelgiant į

  • (x0, ir0) = (1, 2)
  • (x1, ir1) = (3, 4)

Pirmosios eilės Lagranžo interpoliacijos formulė yra

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Esant x = 2

ir =~frac{(2-3)}{(1-3)} imes 2+frac{(2-1)}{(3-1)} imes 4

y = (-2/-2) + (4/2)

y = 1 + 2 = 3

Y reikšmė, kai x = 2, yra 3

sąrašą į masyvą java

2 pavyzdys: suraskite y reikšmę, kai x = 5 tam tikram taškų rinkiniui (9, 2), (3, 10)

Sprendimas:

Atsižvelgiant į

  • (x0, ir0) = (9, 2)
  • (x1, ir1) = (3, 10)

Pirmosios eilės Lagranžo interpoliacijos formulė yra

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Kai x = 5

y~=~frac{(5-3)}{(9-3)} imes 2+frac{(5-9)}{(3-9)} imes 10

y = (4/6) + (-40/-6)

y = (2/3) + (20/3)

y = 22/3 = 7,33

Y reikšmė, kai x = 5, yra 7,33

3 pavyzdys: suraskite y reikšmę, kai x = 1 tam tikram taškų rinkiniui (1, 6), (3, 4), (2, 5)

Sprendimas:

Atsižvelgiant į

  • (x0, ir0) = (1, 6)
  • (x1, ir1) = (3, 4)
  • (x2, ir2) = (2, 5)

Antros eilės Lagranžo interpoliacijos formulė yra

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1) -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

Kai x = 1

y~=~frac{(1-3)(1-2)}{(1-3)(1-2)} imes 6+frac{(1-1)(1-2)}{( 3-1)(3-2)}kartai 4+frak{(1-1)(1-3)}{(2-1)(2-3)}kartai 5 y~=~ frac{(-2)(-1)}{(-2)(-1)} imes 6+frac{(0)(-1)}{(2)(1)} imes 4+frac {(0)(-2)}{(1)(-1)} imes 5

y = (12/2) + 0 + 0

y = 6

Y reikšmė, kai x = 1, yra 6

4 pavyzdys: suraskite y reikšmę, kai x = 10 nurodytai taškų rinkiniui (9, 6), (3, 5), (1, 12)

Sprendimas:

Atsižvelgiant į

  • (x0, ir0) = (9, 6)
  • (x1, ir1) = (3, 5)
  • (x2, ir2) = (1, 12)

Antros eilės Lagranžo interpoliacijos formulė yra

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1) -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

Kai x = 10

y~=~frac{(10-3)(10-1)}{(9-3)(9-1)} imes 6+frac{(10-9)(10-1)}{( 3-9)(3-1)} imes 5+frac{(10-9)(10-3)}{(1-9)(1-3)} imes 12 y~=~ frac{(7)(9)}{(6)(8)} imes 6+frac{(1)(9)}{(-6)(2)} imes 5+frac{(1) (7)}{(-8)(-2)} imes 12

y = (63/8) + (-15/4) + (21/4)

y = (63-30 + 42)/8

y = 75/8 = 9,375

Y reikšmė, kai x = 10, yra 9,375

5 pavyzdys: suraskite y reikšmę, kai x = 7 tam tikram taškų rinkiniui (1, 10), (2, 4), (3, 4), (5, 7)

Sprendimas:

Atsižvelgiant į

  • (x0, ir0) = (1, 10)
  • (x1, ir1) = (2, 4)
  • (x2, ir2) = (3, 4)
  • (x3, ir3) = (5, 7)

Trečios eilės Lagranžo interpoliacijos formulė yra

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0) )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1) )(x_3-x_2)} imes y_3

Kai x = 7

y~=~frac{(7-2)(7-3)(7-5)}{(1-2)(1-3)(1-5)} imes 10+frac{(7- 1)(7-3)(7-5)}{(2-1)(2-3)(2-5)}kartai 4+frak{(7-1)(7-2)(7- 5)}{(3-1)(3-2)(3-5)} imes 4+frac{(7-1)(7-2)(7-3)}{(5-1)( 5-2)(5-3)} imes 7 y~=~frac{(5)(4)(2)}{(-1)(-2)(-4)} imes 10+ frac{(6)(4)(2)}{(1)(-1)(-3)} imes 4+frac{(6)(5)(2)}{(2)(1) (-2)}kartai 4+frak{(6)(5)(4)}{(4)(3)(2)}kartai 7

y = –50 + 64 – 60 + 35

y = 99–110 = -vienuolika

Y reikšmė, kai x = 7, yra -11

6 pavyzdys: suraskite y reikšmę, kai x = 10 nurodytai taškų rinkiniui (5, 12), (6, 13), (7, 14), (8, 15)

Sprendimas:

Atsižvelgiant į

  • (x0, ir0) = (5, 12)
  • (x1, ir1) = (6, 13)
  • (x2, ir2) = (7, 14)
  • (x3, ir3) = (8, 15)

Trečios eilės Lagranžo interpoliacijos formulė yra

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0) )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1) )(x_3-x_2)} imes y_3

Kai x = 10,

y~=~frac{(10-6)(10-7)(10-8)}{(5-6)(5-7)(5-8)} imes 12+frac{(10- 5)(10-7)(10-8)}{(6-5)(6-7)(6-8)} imes 13+frac{(10-5)(10-6)(10- 8)}{(7-5)(7-6)(7-8)} imes 14+frac{(10-5)(10-6)(10-7)}{(8-5)( 8-6)(8-7)} imes 15 y~=~frac{(4)(3)(2)}{(-1)(-2)(-3)} imes 12+ frac{(5)(3)(2)}{(1)(-1)(-2)} imes 13+frac{(5)(4)(2)}{(2)(1) (-1)} imes 14+frac{(5)(4)(3)}{(3)(2)(1)} imes 15

y = -48 + 195 – 280 + 150

y = 17

Y reikšmė, kai x = 10, yra 17

7 pavyzdys: suraskite y reikšmę, kai x = 0 duotoje taškų aibėje (-2, 5), (1, 7)

Sprendimas:

Atsižvelgiant į

  • (x0, ir0) = (-2, 5)
  • (x1, ir1) = (1, 7)

Pirmosios eilės Lagranžo interpoliacijos formulė yra

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Kai x = 0,

y~=~frac{(0-1)}{(-2-1)} imes 5+frac{(0+2)}{(1+2)} imes 7

y = (5/3) + (14/3)

y = 19/3 = 6,33

Y reikšmė, kai x = 0, yra 6,33

DUK apie Lagranžo interpoliacijos formulę

1. Kas yra Lagranžo interpoliacijos formulė?

Lagranžo interpoliacijos formulė yra formulė, naudojama norint rasti bet kurio nepriklausomo kintamojo priklausomo funkcijos kintamojo vertę, net jei pati funkcija nėra pateikta.

2. Kokie yra Lagranžo interpoliacijos formulės pritaikymai?

Lagrangeso formulė yra įvairiai pritaikyta šiuolaikiniuose matematikos ir duomenų moksluose,

kas yra f5 klaviatūroje
  • Jis naudojamas prie AI modelio „Traning“.
  • Jis naudojamas vaizdo apdorojimui.
  • Jis naudojamas 3D ir aukštesnių kreivių grafavimui ir kt.

3. Kas yra pirmosios eilės Lagranžo interpoliacijos formulė?

Pirmosios eilės Lagranso interpoliacijos formulė yra

f(x) = (x – x 1 )/(x 0 – x 1 )×f 0 + (x – x 0 )/(x 1 – x 0 )×f 1

4. Kas yra antros eilės Lagranžo interpoliacijos formulė?

Antrosios eilės Lagranso interpoliacijos formulė yra

f(x) = [(x – x 1 )(x – x 2 )/(x 0 – x 1 )(x 0 – x 2 )]×f 0 + [(x – x 0 )(x – x 2 )/(x 1 – x 0 )(x 1 – x 2 )]×f 1 + [(x – x 0 )(x – x 1 )/(x 2 – x 0 )(x 2 – x 2 )]×f 0