Ar kiekvienas stačiakampis yra rombas? Stačiakampis yra dvimatė geometrinė figūra, pavaizduota keturiomis kraštinėmis ir keturiais kampais. Stačiakampis turi tokias kraštines, kad priešingų kraštinių ilgis yra lygus ir šios kraštinės yra lygiagrečios viena kitai. Šalys dalijasi kampu nuo gretimų kraštų su 90° kampu tarp jų. Todėl stačiakampyje yra keturi stačiakampiai.

Turinys
- Stačiakampis
- Rombas
- Ar kiekvienas stačiakampis yra rombas?
- Klausimų pavyzdžiai – ar kiekvienas stačiakampis yra rombas?
Stačiakampis
Stačiakampio savybės pateiktos žemiau:
- Jis turi keturis kraštus ir keturis kampus, vadinamus viršūnėmis.
- Stačiakampio įstrižainės dalija viena kitą.
- Stačiakampio plotas yra lygus jo ilgio ir pločio sandaugai.
- Kiekviena viršūnė turi kampą, lygų 90O
- Priešingos stačiakampio kraštinės yra lygios ir lygiagrečios viena kitai.
- Perimetras yra lygus dvigubai jo ilgio ir pločio sumai.
- Visų vidinių kampų suma lygi 360 laipsnių
Stačiakampio perimetras
Bendras poslinkis, padengtas einant per stačiakampio ribą, gali būti vadinamas perimetru. Kadangi ilgis ir plotis žymimi ilgio vienetu, perimetras taip pat matuojamas ilgio vienetu.
Perimetras gali būti žymimas taip,
Perimetras, P = 2 (ilgis + plotis)
Stačiakampio plotas
Sritis, kurią plokštumoje dengia dvimatė geometrinė figūra, vadinama figūros plotu. Taigi, stačiakampio plotas yra plotas, įtrauktas į jo ribas. Jis matuojamas kvadratiniais vienetais. Plotas yra lygus stačiakampio ilgio ir pločio sandaugai.
Plotas gali būti žymimas taip,
Plotas, A = ilgio × pločio kv. vienetai
Stačiakampio formulės įstrižainė
Bet kurios geometrinės figūros įstrižainės jungia alternatyvias viršūnes. Stačiakampio įstrižainių ilgį galima apskaičiuoti pagal šią formulę, pažymėtą d,
d = sqrt{( l^2 + w^2)} kur,
l = stačiakampio ilgis
w = stačiakampio plotis
Skaitykite išsamiai: Stačiakampio savybės: apibrėžimas, formulės, pavyzdžiai
Rombas
Rombas taip pat žinomas kaip keturkampis keturkampis. Tai laikoma ypatingu lygiagretainio atveju. Rombą sudaro lygiagrečios priešingos pusės ir vienodi priešingi kampai. Rombas taip pat žinomas deimanto arba rombo deimanto pavadinimu. Rombą sudaro visos vienodo ilgio rombo kraštinės. Taip pat rombo įstrižainės viena kitą dalija stačiu kampu.
Rombo savybės
Rombas turi šias savybes:
- Rombą sudaro visos lygios pusės.
- Rombo įstrižainės viena kitą dalija stačiu kampu.
- Priešingos rombo pusės iš prigimties yra lygiagrečios.
- Dviejų gretimų rombo kampų suma lygi 180O.
- Rombo viduje nėra užrašo apskritimo.
- Aplink rombą nėra apibrėžiančio apskritimo.
- Dėl rombo įstrižainių susidaro keturi stačiakampiai trikampiai.
- Šie trikampiai sutampa vienas su kitu.
- Priešingi rombo kampai yra lygūs.
- Kai sujungiate rombo kraštinių vidurio tašką, susidaro stačiakampis.
- Sujungus pusės įstrižainės vidurio taškus, susidaro kitas rombas.
Rombo perimetras
Rombo perimetras apibrėžiamas kaip bendras jo ribų, sudarančių figūrą, ilgis. Jis taip pat gali būti žymimas kaip bendra keturių rombo kraštinių ilgio suma. Rombo perimetras apibrėžiamas taip:
Perimetras, P = 4a vnt
kur rombo įstrižainės žymimos d1& d2o „a“ yra pusė.
Rombo sritis
Rombo plotas apibrėžiamas kaip sritis, uždaryta dvimatėje plokštumoje. Rombo plotas yra lygus rombo įstrižainių sandaugai, padalytai iš 2. Rombo plotą galima apibrėžti pagal šią formulę :
Plotas, A =
frac{(d_1 imes d_2)}{2} kv.vntkur1ir d2yra rombo įstrižainės.
Galime nesunkiai pastebėti, kad kiekvienas rombas yra lygiagretainis, tačiau atvirkščiai – netiesa. Kvadratas gali būti laikomas ypatingu rombo atveju, nes jame yra keturios vienodo ilgio kraštinės. Kvadratas turi visus stačius kampus. Tačiau visi rombo kampai nebūtinai yra stačiakampiai . Galiausiai rombas, turintis stačių kampų, gali būti laikomas kvadratu. Todėl galime pasakyti, kad
- Visi rombai yra lygiagretainiai.
- Visi lygiagretainiai nėra rombai.
- Visi rombai nėra kvadratai.
- Visi kvadratai yra rombai.
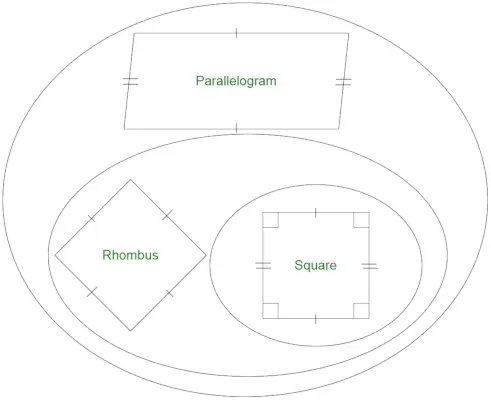
Ar kiekvienas stačiakampis yra rombas?
Stačiakampis yra geometrinė figūra, kurios kraštinės nėra lygios. Kvadratas yra ypatingas stačiakampio su visomis lygiomis kraštinėmis atvejis. Kadangi, kaip žinome, rombas turi visas lygias puses. Stačiakampių ir rombų aibės susikerta tik kvadratų atveju. Todėl stačiakampis nėra rombas.
java patikrinimas yra niekinis

Kodėl rombas yra stačiakampis?
Rombas yra ypatingas stačiakampio atvejis. Kadangi žinome, kad rombo įstrižainės susikerta vienodais kampais, o stačiakampio įstrižainės yra vienodo ilgio. Sujungus rombo kraštinių vidurio taškus, susidaro stačiakampis.
Skaityti daugiau: Kodėl rombas nėra kvadratas?
Klausimų pavyzdžiai – ar kiekvienas stačiakampis yra rombas?
1 klausimas. Apskaičiuokite stačiakampio rėmo, kurio plotas yra 6 coliai, plotą ilgio ir 3 colių pločio.
Sprendimas:
Kadangi mes žinome,
Stačiakampio plotas = (ilgis × plotis) kvadratiniai vienetai.
Pakeitę reikšmes, gauname,
stačiakampio rėmo plotas = 6 × 3 = 18 kvadratinių colių
2 klausimas. Raskite stačiakampio, kurio ilgis yra atitinkamai 12 cm, o plotis – 8 cm, įstrižainės ilgį.
Sprendimas:
Mes žinome,
Įstrižainės ilgis,
D =
sqrt{ L^2+W^2} ⇒ D =
sqrt{12^2+8^2} ⇒ D =
sqrt{144 + 64} ⇒ D = √208
⇒ D = 4√3
3 klausimas. Raskite rombo, kurio dvi įstrižainės ilgis d, plotą 1 ir d 2 būti atitinkamai 6 cm ir 12 cm.
Sprendimas:
Mes turime,
Įstrižainė d1= 6 cm
Įstrižainė d2= 12 cm
Rombo plotas pateikiamas taip,
A =
frac{(d_1 imes d_2)}{2} kv.vntA =
frac{( 6 imes 12)}{2} A =
frac{72}{2} A = 36 cm2
Todėl rombo plotas = 36 cm2.
4 klausimas. Kuo skiriasi rombas ir stačiakampis?
Sprendimas:
| Nuosavybė | Rombas | Stačiakampis |
| Šonai | Lygios pusės. | Priešingos pusės yra lygios. |
| Įstrižainės | Įstrižainės dalija viena kitą 90° kampu. Įstrižainės sudaro stačius kampus centre. | Įstrižainės dalija viena kitą skirtingais kampais. Vienas kampas yra bukas kampas, o kitas - smailusis. Įstrižainės sudaro skirtingus kampus centre - bukas ir smailus kampas. |
| Kampai | Priešingi kampai yra lygūs. Gretimi kampai sudaro 180°. | Priešingi ir gretimi kampai yra lygūs. Kampas, sudarytas iš gretimų stačiakampio kraštinių, yra 90°. |
