„MIN-HEAP“ ĮVADAS – DUOMENŲ STRUKTŪROS IR ALGORITMŲ VADOVĖLIAI

A Min-Heap apibrėžiamas kaip tipas Krūvos duomenų struktūra yra dvejetainio medžio tipas, kuris kompiuterių moksle dažniausiai naudojamas įvairiems tikslams, įskaitant duomenų rūšiavimą, paiešką ir tvarkymą.
„Min-Heap“ įvadas – duomenų struktūros ir algoritmų vadovėliai
Min-Heap paskirtis ir naudojimo atvejai:
Prioritetinės eilės diegimas: Vienas iš pagrindinių krūvos duomenų struktūros naudojimo būdų yra prioritetinių eilių įgyvendinimas.
Dijkstros algoritmas : Dijkstra algoritmas yra trumpiausio kelio algoritmas, kuris suranda trumpiausią kelią tarp dviejų grafiko mazgų. Mažiausiu atstumu nuo šaltinio mazgo galima sekti nelankytus mazgus.
Rūšiavimas: Minimali krūva gali būti naudojama kaip rūšiavimo algoritmas, siekiant efektyviai rūšiuoti elementų rinkinį didėjančia tvarka.
Vidutinė išvada: Norint efektyviai rasti skaičių srauto medianą, galima naudoti min. Galime naudoti vieną min krūvą didesnei skaičių pusei saugoti ir vieną didžiausią krūvą mažesnei pusei saugoti. Mediana bus min krūvos šaknis.
Min-Heap duomenų struktūra skirtingomis kalbomis:

1. Min-Heap C++

Minimąją krūvą galima įdiegti naudojant prioriteto_eilė konteineris iš standartinės šablonų bibliotekos (STL). The prioriteto_eilė konteineris yra konteinerio adapterio tipas, suteikiantis galimybę saugoti elementus į eilę panašioje duomenų struktūroje, kurioje kiekvienas elementas turi su juo susietą prioritetą.
Sintaksė :
C++
 priority_queue < int, vector , didesnis > minH;>> 2. Min-Heap Java 
Java programoje mini krūva gali būti įdiegta naudojant    PriorityQueue    klasė nuo    java.util paketą    . PriorityQueue klasė yra prioritetinė eilė, kuri suteikia galimybę saugoti elementus į eilę panašioje duomenų struktūroje, kurioje kiekvienas elementas turi su juo susietą prioritetą.
     Sintaksė    :
10 iš 40
JavaMin-Heap Python  Python programoje mini krūva gali būti įdiegta naudojant  heapq  modulis, kuriame pateikiamos krūvos įgyvendinimo funkcijos. Tiksliau,    heapq    modulis suteikia galimybę kurti ir valdyti krūvos duomenų struktūras.
 
 

     Sintaksė:    
PythonC# kalboje mini krūva gali būti įdiegta naudojant PriorityQueue klasę iš Sistema.Kolekcijos.Bendroji vardų erdvė . PriorityQueue klasė yra prioritetinė eilė, kuri suteikia galimybę saugoti elementus į eilę panašioje duomenų struktūroje, kurioje kiekvienas elementas turi su juo susietą prioritetą.
     Sintaksė:    
C# var minHeap = new PriorityQueue ();>> 5. Min-heap JavaScript
Minimali krūva yra dvejetainis medis, kuriame kiekvienas mazgas turi mažesnę ar lygią reikšmę jo vaikams. „JavaScript“ galite įdiegti minimalią krūvą naudodami masyvą, kur pirmasis elementas žymi šakninį mazgą, o mazgo antrinės dalys indekse    i    yra prie indeksų    2i+1    ir    2i+2.    
     Sintaksė:    
JavaScript    Skirtumas tarp „Min Heap“ ir „Max Heap“:        
 Min. krūva
 Max Heap
 
 1.
 Min-Heap raktas, esantis šakniniame mazge, turi būti mažesnis arba lygus tarp visų antrinių raktų.
 „Max-Heap“ šakniniame mazge esantis raktas turi būti didesnis arba lygus tarp visų antrinių raktų.
 
 2.
 Min-Heap minimalus pagrindinis elementas yra šaknyje.
 Max-Heap didžiausias pagrindinis elementas yra šaknyje.
 
 3.
 Min-Heap naudoja didėjantį prioritetą.
 Max-Heap naudoja mažėjantį prioritetą.
 
 4.
 Konstruojant „Min-Heap“ pirmenybė teikiama mažiausiam elementui.
java sujungimo eilutės
 „Max-Heap“ konstrukcijoje pirmenybė teikiama didžiausiam elementui.
 
 5.
 Min-Heap mažiausias elementas yra pirmasis, kuris iškeliamas iš krūvos.
 Max-Heap didžiausias elementas yra pirmasis, kuris ištraukiamas iš krūvos.
 
Vidinis „Min-Heap“ duomenų struktūros įgyvendinimas:
 A    Minimali krūva paprastai vaizduojama kaip masyvas    .
 Šakninis elementas bus adresu    Arr[0]    .
Bet kuriam i-jam mazgui    Arr[i]    :    Arr[(i -1) / 2]    grąžina pirminį mazgą.
    Arr[(2 * i) + 1]    grąžina savo kairįjį antrinį mazgą.
    Arr[(2 * i) + 2]    grąžina savo dešinįjį antrinį mazgą.
Vidinis „Min-Heap“ diegimas reikalauja 3 pagrindinių žingsnių:
     Įdėjimas    : Norėdami įterpti elementą į minimalią krūvą, pirmiausia pridedame elementą prie masyvo pabaigos, o tada koreguojame krūvos ypatybę pakartotinai keisdami elementą su pirminiu elementu, kol jis bus tinkamoje padėtyje.
    Ištrynimas    : Norėdami pašalinti minimalų elementą iš min krūvos, pirmiausia sukeičiame šakninį mazgą su paskutiniu masyvo elementu, pašaliname paskutinį elementą ir koreguojame krūvos ypatybę pakartotinai keisdami elementą su mažiausiu antriniu elementu, kol jis atsidurs masyvo elemente. teisinga padėtis.
    Sukrauti    : norint sukurti minimalią krūvą iš nerūšiuoto masyvo, galima naudoti krūvos didinimo operaciją.
Operacijos su minimalios krūvos duomenų struktūra ir jų įgyvendinimas:
Štai keletas įprastų operacijų, kurias galima atlikti su krūvos duomenų struktūra,
 1. Įterpimas į Min-Heap duomenų struktūrą :
Elementai gali būti įterpti į krūvą taikant panašų metodą, kaip aprašyta anksčiau, norint ištrinti. Idėja tokia:
 Įterpimo į mažąją krūvą operacija apima šiuos veiksmus:
Pridėkite naują elementą į krūvos pabaigą kitoje galimoje pozicijoje paskutiniame medžio lygyje.
Palyginkite naują elementą su pirminiu elementu. Jei pirminis elementas yra didesnis nei naujasis elementas, pakeiskite juos.
Kartokite 2 veiksmą, kol pirminis elementas bus mažesnis arba lygus naujam elementui, arba kol naujas elementas pasieks medžio šaknį.
Naujas elementas dabar yra tinkamoje padėtyje min. krūvoje, o krūvos savybė yra patenkinta.
    Iliustracija:    
      Tarkime, kad krūva yra mažoji krūva:    
 Įterpimas į Min-Heap
 
Įterpimo operacijos įgyvendinimas „Min-Heap“:
C++ #include  #include  using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int reikšmė) { // Įtraukite naują elementą į krūvos pabaigą.push_back(value);  // Gauti paskutinio elemento indeksą int index = heap.size() - 1;  // Palyginkite naują elementą su pirminiu elementu ir pakeiskite, jei reikia //, while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]);  // Perkelti medį aukštyn į dabartinio elemento pirminį // elemento indeksą = (indeksas - 1) / 2;  } } // Pagrindinė funkcija, skirta funkcijai insert_min_heap patikrinti int main() { vektorius krūva;  int reikšmės[] = { 10, 7, 11, 5, 4, 13 };  int n = dydis(reikšmės) / dydis(reikšmės[0]);  už (int i = 0; i< n; i++) {  insert_min_heap(heap, values[i]);  cout << 'Inserted ' << values[i]  << ' into the min-heap: ';  for (int j = 0; j < heap.size(); j++) {  cout << heap[j] << ' ';  }  cout << endl;  }  return 0; }>
 Java import java.util.*; public class GFG {  // Function to insert a new element into the min-heap  public static void insertMinHeap(int[] heap, int size,  int value)  {  // Add the new element to the end of the heap  heap[size] = value;  // Get the index of the last element  int index = size;  // Compare the new element with its parent and swap  // if necessary  while (index>0 && krūva[(indeksas - 1) / 2]> krūva[indeksas]) { apsikeitimas(krūva, indeksas, (indeksas - 1) / 2);  // Perkelti medį aukštyn į dabartinio elemento pirminį // elemento indeksą = (indeksas - 1) / 2;  } } // Funkcija sukeisti du elementus masyve public static void swap(int[] arr, int i, int j) { int temp = arr[i];  arr[i] = arr[j];  arr[j] = temp;  } // Pagrindinė funkcija, skirta funkcijai insertMinHeap testuoti public static void main(String[] args) { int[] heap = new int[6];  int[] reikšmės = { 10, 7, 11, 5, 4, 13 };  int dydis = 0;  už (int i = 0; i< values.length; i++) {  insertMinHeap(heap, size, values[i]);  size++;  System.out.print('Inserted ' + values[i]  + ' into the min-heap: ');  for (int j = 0; j < size; j++) {  System.out.print(heap[j] + ' ');  }  System.out.println();  }  } }>
 Python3 def insert_min_heap(heap, value): # Add the new element to the end of the heap heap.append(value) # Get the index of the last element index = len(heap) - 1 # Compare the new element with its parent and swap if necessary while index>0 ir krūva[(rodyklė - 1) // 2]> krūva[rodyklė]: krūva[rodyklė], krūva[(rodyklė - 1) // 2] = krūva[(indeksas - 1) // 2], krūva[ index] # Perkelkite medį aukštyn į dabartinio elemento pirminį indeksą = (indeksas - 1) // 2 heap = [] reikšmės = [10, 7, 11, 5, 4, 13], jei reikia reikšmės reikšmėse: insert_min_heap( heap, value) print(f'Įterpta {value} į min-heap: {heap}')>
 C# using System; using System.Collections.Generic; public class Program {  // Function to insert a new element into the min-heap  static void InsertMinHeap(List krūva, int reikšmė) { // Įtraukite naują elementą į krūvos krūvos pabaigą.Add(value);  // Gaukite paskutinio elemento indeksą int index = heap.Count - 1;  // Palyginkite naują elementą su pirminiu elementu ir pakeiskite // jei reikia, while (index> 0 && heap[(index - 1) / 2]> heap[index]) { int temp = heap[index];  krūva[indeksas] = krūva[(indeksas - 1) / 2];  krūva [(indeksas - 1) / 2] = temp;  // Perkelti medį aukštyn į dabartinio elemento pirminį // elemento indeksą = (indeksas - 1) / 2;  } } // Pagrindinė funkcija InsertMinHeap funkcijai patikrinti public static void Main() { Sąrašas krūva = naujas sąrašas ();  int[] reikšmės = { 10, 7, 11, 5, 4, 13 };  foreach(int reikšmė reikšmėse) { InsertMinHeap(heap, value);  Console.Write('Įterpta ' + reikšmė + ' į mažąją krūvą: ');  foreach(int elementas krūvoje) { Console.Write(element + ' ');  } Console.WriteLine();  } } }>
 Javascript function insertMinHeap(heap, value) {  heap.push(value);  let index = heap.length - 1;  let parentIndex = Math.floor((index - 1) / 2);  while (index>0 && heap[parentIndex]> heap[index]) { [heap[index], heap[parentIndex]] = [heap[parentIndex], heap[index]];  indeksas = parentIndex;  parentIndex = Math.floor((indeksas - 1) / 2);  } } // Naudojimo pavyzdys const heap = []; const reikšmės = [10, 7, 11, 5, 4, 13]; for (const reikšmių reikšmė) { insertMinHeap(heap, value);  console.log(`Įterpta ${value} į min-heap: ${heap}`); }>
   
  Išvestis  Inserted 10 into the min-heap: 10 Inserted 7 into the min-heap: 7 10 Inserted 11 into the min-heap: 7 10 11 Inserted 5 into the min-heap: 5 7 11 10 Inserted 4 into the min-heap: 4 5 11 10 7 Inser...>
     Laiko sudėtingumas: O(log(n)) (    kur n yra elementų skaičius krūvoje    )     
    Pagalbinė erdvė:    O(n)
 2. Ištrynimas Min-Heap duomenų struktūroje :
Mažiausio elemento (šaknies) pašalinimas iš min krūvos. Šaknis pakeičiamas paskutiniu elementu krūvoje, o tada krūvos ypatybė atkuriama pakeičiant naują šaknį su mažiausiu antruoju, kol tėvas bus mažesnis už abu vaikus arba kol nauja šaknis pasieks lapo mazgą.
 Pakeiskite šaknį arba elementą, kurį norite ištrinti, paskutiniu elementu.
Ištrinkite paskutinį elementą iš krūvos.
Kadangi paskutinis elementas dabar yra pagrindinio mazgo vietoje. Taigi, jis gali nesilaikyti krūvos savybės. Todėl surinkite paskutinį mazgą, esantį šaknies vietoje.
    Iliustracija    :
      Tarkime, kad krūva yra mažoji krūva:    
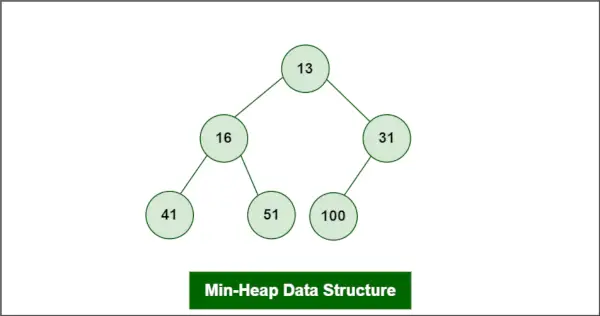
  Min-Heap duomenų struktūra
     Elementas, kurį reikia ištrinti, yra root, ty 13.    
     Procesas    :
 Paskutinis elementas yra 100.
     1 žingsnis:         Paskutinį elementą pakeiskite šaknimi ir ištrinkite.    
pašalinti angular cli
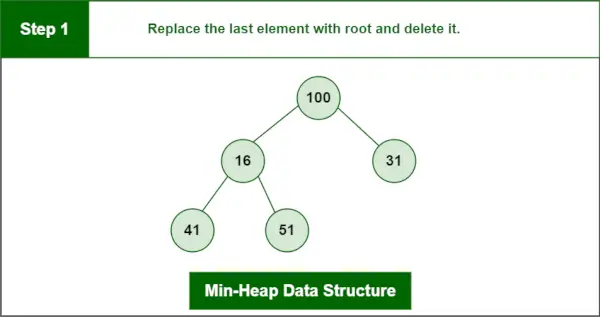
  Min-Heap duomenų struktūra
     2 žingsnis    :    Sukaupti šaknį.    
 Galutinė krūva:
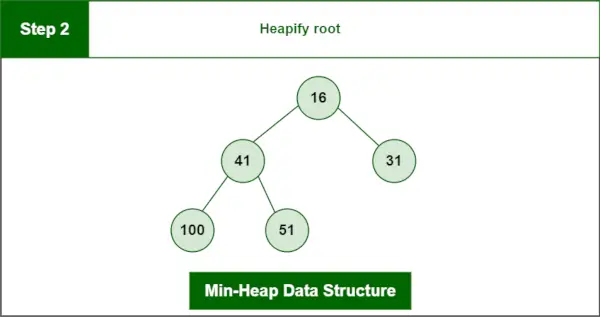
  Min-Heap duomenų struktūra
  
 
Ištrynimo operacijos įgyvendinimas „Min-Heap“:
C++ #include  #include  using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int reikšmė) { // Įtraukite naują elementą į krūvos pabaigą.push_back(value);  // Gauti paskutinio elemento indeksą int index = heap.size() - 1;  // Palyginkite naują elementą su pirminiu elementu ir pakeiskite, jei reikia //, while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]);  // Perkelti medį aukštyn į dabartinio elemento pirminį // elemento indeksą = (indeksas - 1) / 2;  } } // Funkcija pašalinti mazgą iš min-heap void delete_min_heap(vector & heap, int reikšmė) { // Rasti elemento, kurį norite ištrinti, indeksą int index = -1;  už (int i = 0; i< heap.size(); i++) {  if (heap[i] == value) {  index = i;  break;  }  }  // If the element is not found, return  if (index == -1) {  return;  }  // Replace the element to be deleted with the last  // element  heap[index] = heap[heap.size() - 1];  // Remove the last element  heap.pop_back();  // Heapify the tree starting from the element at the  // deleted index  while (true) {  int left_child = 2 * index + 1;  int right_child = 2 * index + 2;  int smallest = index;  if (left_child < heap.size()  && heap[left_child] < heap[smallest]) {  smallest = left_child;  }  if (right_child < heap.size()  && heap[right_child] < heap[smallest]) {  smallest = right_child;  }  if (smallest != index) {  swap(heap[index], heap[smallest]);  index = smallest;  }  else {  break;  }  } } // Main function to test the insert_min_heap and // delete_min_heap functions int main() {  vector krūva;  int reikšmės[] = { 13, 16, 31, 41, 51, 100 };  int n = dydis(reikšmės) / dydis(reikšmės[0]);  už (int i = 0; i< n; i++) {  insert_min_heap(heap, values[i]);  }  cout << 'Initial heap: ';  for (int j = 0; j < heap.size(); j++) {  cout << heap[j] << ' ';  }  cout << endl;  delete_min_heap(heap, 13);  cout << 'Heap after deleting 13: ';  for (int j = 0; j < heap.size(); j++) {  cout << heap[j] << ' ';  }  cout << endl;  return 0; }>
 Java import java.util.*; public class GFG {  // Function to insert a new element into the min-heap  public static void insertMinHeap(List krūva, int reikšmė) { // Įtraukite naują elementą į krūvos pabaigą heap.add(value);  // Gauti paskutinio elemento indeksą int index = heap.size() - 1;  // Palyginkite naują elementą su pirminiu elementu ir pakeiskite // jei reikia, while (index> 0 && heap.get((index - 1) / 2)> heap.get(index)) { Collections.swap(heap, index, (indeksas - 1) / 2);  // Perkelti medį aukštyn į dabartinio // elemento pirminį indeksą = (indeksas - 1) / 2;  } } // Funkcija pašalinti mazgą iš min-heap viešosios statinės void deleteMinHeap(List krūva, int reikšmė) { // Raskite naikinamo elemento indeksą int index = -1;  už (int i = 0; i< heap.size(); i++) {  if (heap.get(i) == value) {  index = i;  break;  }  }  // If the element is not found, return  if (index == -1) {  return;  }  // Replace the element to be deleted with the last  // element  heap.set(index, heap.get(heap.size() - 1));  // Remove the last element  heap.remove(heap.size() - 1);  // Heapify the tree starting from the element at the  // deleted index  while (true) {  int leftChild = 2 * index + 1;  int rightChild = 2 * index + 2;  int smallest = index;  if (leftChild < heap.size()  && heap.get(leftChild)  < heap.get(smallest)) {  smallest = leftChild;  }  if (rightChild < heap.size()  && heap.get(rightChild)  < heap.get(smallest)) {  smallest = rightChild;  }  if (smallest != index) {  Collections.swap(heap, index, smallest);  index = smallest;  }  else {  break;  }  }  }  // Main function to test the insertMinHeap and  // deleteMinHeap functions  public static void main(String[] args)  {  List krūva = naujas ArrayList ();  int[] reikšmės = { 13, 16, 31, 41, 51, 100 };  int n = reikšmės.ilgis;  už (int i = 0; i< n; i++) {  insertMinHeap(heap, values[i]);  }  System.out.print('Initial heap: ');  for (int j = 0; j < heap.size(); j++) {  System.out.print(heap.get(j) + ' ');  }  System.out.println();  deleteMinHeap(heap, 13);  System.out.print('Heap after deleting 13: ');  for (int j = 0; j < heap.size(); j++) {  System.out.print(heap.get(j) + ' ');  }  System.out.println();  } }>
 Python3 def insert_min_heap(heap, value): heap.append(value) index = len(heap) - 1 while index>0 ir krūva[(rodyklė - 1) // 2]> krūva[rodyklė]: krūva[rodyklė], krūva[(rodyklė - 1) // 2] = krūva[(indeksas - 1) // 2], krūva[ indeksas] indeksas = (indeksas - 1) // 2 def delete_min_heap(heap, value): index = -1 for i diapazone(len(heap)): if heap[i] == reikšmė: index = i break if index == -1: grąžinti krūvą[indeksas] = krūva[-1] heap.pop(), o tiesa: kairysis_vaikas = 2 * indeksas + 1 dešinysis_vaikas = 2 * indeksas + 2 mažiausias = indeksas, jei kairysis_vaikas< len(heap) and heap[left_child] < heap[smallest]: smallest = left_child if right_child < len(heap) and heap[right_child] < heap[smallest]: smallest = right_child if smallest != index: heap[index], heap[smallest] = heap[smallest], heap[index] index = smallest else: break heap = [] values = [13, 16, 31, 41, 51, 100] for value in values: insert_min_heap(heap, value) print('Initial heap:', heap) delete_min_heap(heap, 13) print('Heap after deleting 13:', heap)>
 C# using System; using System.Collections.Generic; class MinHeap {  private List krūva = naujas sąrašas ();  public void Insert(int value) { heap.Add(value);  int indeksas = krūva.Skaičius - 1;  while (indeksas> 0 && krūva[(indeksas - 1) / 2]> krūva[indeksas]) { Sukeisti(indeksas, (indeksas - 1) / 2);  indeksas = (indeksas - 1) / 2;  } } public void Ištrinti(int reikšmė) { int indeksas = krūva.IndexOf(value);  if (indeksas == -1) { return;  } krūva[indeksas] = krūva[krūva.Skaičius - 1];  krūva.RemoveAt(heap.Count - 1);  while (true) { int leftVaikas = 2 * indeksas + 1;  int rightChild = 2 * indeksas + 2;  int mažiausias = indeksas;  jei (leftChild< heap.Count  && heap[leftChild] < heap[smallest]) {  smallest = leftChild;  }  if (rightChild < heap.Count  && heap[rightChild] < heap[smallest]) {  smallest = rightChild;  }  if (smallest != index) {  Swap(index, smallest);  index = smallest;  }  else {  break;  }  }  }  private void Swap(int i, int j)  {  int temp = heap[i];  heap[i] = heap[j];  heap[j] = temp;  }  public void Print()  {  for (int i = 0; i < heap.Count; i++) {  Console.Write(heap[i] + ' ');  }  Console.WriteLine();  } } class Program {  static void Main(string[] args)  {  MinHeap heap = new MinHeap();  int[] values = { 13, 16, 31, 41, 51, 100 };  for (int i = 0; i < values.Length; i++) {  heap.Insert(values[i]);  }  Console.Write('Initial heap: ');  heap.Print();  heap.Delete(13);  Console.Write('Heap after deleting 13: ');  heap.Print();  } }>
 Javascript function insertMinHeap(heap, value) {  // Add the new element to the end of the heap  heap.push(value);  // Get the index of the last element  let index = heap.length - 1;  // Compare the new element with its parent and swap if necessary  for (let flr = Math.floor((index - 1) / 2); index>0 && heap[flr]> heap[index]; flr = Math.floor((indeksas - 1) / 2)) { [krūva[indeksas], krūva[flr]] = [ krūva[flr], krūva[indeksas], ];  // Perkelti medį aukštyn į dabartinio elemento pirminį indeksą = Math.floor((index - 1) / 2);  } } function deleteMinHeap(heap, value) { // Raskite trinamo elemento indeksą tegul index = -1;  for (tegul i = 0; i< heap.length; i++) {  if (heap[i] == value) {  index = i;  break;  }  }  // If the element is not found, return  if (index == -1) {  return;  }  // Replace the element to be deleted with the last element  heap[index] = heap[heap.length - 1];  // Remove the last element  heap.pop();  // Heapify the tree starting from the element at the deleted index  while (true) {  let left_child = 2 * index + 1;  let right_child = 2 * index + 2;  let smallest = index;  if (left_child < heap.length && heap[left_child] < heap[smallest]) {  smallest = left_child;  }  if (right_child < heap.length && heap[right_child] < heap[smallest]) {  smallest = right_child;  }  if (smallest != index) {  [heap[index], heap[smallest]] = [heap[smallest], heap[index]];  index = smallest;  } else {  break;  }  } } // Main function to test the insertMinHeap and deleteMinHeap functions let heap = []; let values = [13, 16, 31, 41, 51, 100]; for (let i = 0; i < values.length; i++) {  insertMinHeap(heap, values[i]); } console.log('Initial heap: ' + heap.join(' ')); deleteMinHeap(heap, 13); console.log('Heap after deleting 13: ' + heap.join(' '));>
   
  Išvestis  Initial heap: 13 16 31 41 51 100 Heap after deleting 13: 16 41 31 100 51>
     Laiko sudėtingumas    : O(log n), kur n yra elementų skaičius krūvoje  
    Pagalbinė erdvė:    O(n)
 3. Min-Heap duomenų struktūros peržiūros operacija:
Norint pasiekti minimalų elementą (t. y. krūvos šaknį), grąžinama šakninio mazgo reikšmė. Žvilgtelėjimo į min krūvą laiko sudėtingumas yra O(1).
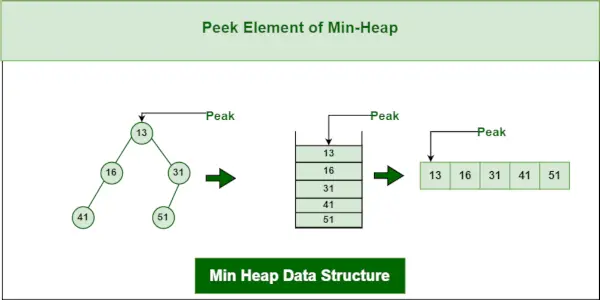
  Minimali krūvos duomenų struktūra
 „Peek“ operacijos įgyvendinimas „Min-Heap“:
C++ #include  #include  #include  using namespace std; int main() {  // Create a max heap with some elements using a  // priority_queue  priority_queue , didesnis > minHeap;  minHeap.push(9);  minHeap.push(8);  minHeap.push(7);  minHeap.push(6);  minHeap.push(5);  minHeap.push(4);  minHeap.push(3);  minHeap.push(2);  minHeap.push(1);  // Gauti piko elementą (t. y. didžiausią elementą) int peakElement = minHeap.top();  // Spausdinti smailės elemento dydį<< 'Peak element: ' << peakElement << std::endl;  return 0; }>
 Java import java.util.PriorityQueue; public class GFG {  public static void main(String[] args)  {  // Create a max heap with some elements using a  // PriorityQueue  PriorityQueue minHeap = new PriorityQueue();  minHeap.add(9);  minHeap.add(8);  minHeap.add(7);  minHeap.add(6);  minHeap.add(5);  minHeap.add(4);  minHeap.add(3);  minHeap.add(2);  minHeap.add(1);  // Gauti piko elementą (t. y. didžiausią elementą) int peakElement = minHeap.peek();  // Spausdinti piko elementą System.out.println('Peak element: ' + peakElement);  } }>>Python3
 C# using System; using System.Collections.Generic; public class GFG {  public static void Main()  {  // Create a min heap with some elements using a  // PriorityQueue  var minHeap = new PriorityQueue ();  minHeap.Enqueue(9);  minHeap.Enqueue(8);  minHeap.Enqueue(7);  minHeap.Enqueue(6);  minHeap.Enqueue(5);  minHeap.Enqueue(4);  minHeap.Enqueue(3);  minHeap.Enqueue(2);  minHeap.Enqueue(1);  // Gauti piko elementą (ty mažiausią elementą) int peakElement = minHeap.Peek();  // Spausdinti piko elementą Console.WriteLine('Peak element: ' + peakElement);  } }>>Javascripta - b); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Gauti piko elementą (ty mažiausią elementą) const peakElement = minHeap.peek(); // Spausdinti piko elementą console.log(`Peak element: ${peakElement}`);>>  
  Išvestis  Peak element: 1>
      Laiko sudėtingumas    : Minimojoje krūvoje, įdiegtoje naudojant masyvą arba sąrašą, smailės elementą galima pasiekti pastoviu laiku, O(1), nes jis visada yra krūvos šaknyje.  
Minimalioje krūvoje, įdiegtoje naudojant dvejetainį medį, smailės elementą taip pat galima pasiekti per O (1) laiką, nes jis visada yra medžio šaknyje.
java loginė
     Pagalbinė erdvė:    O(n)
 4. Min-Heap duomenų struktūros „Heapify“ operacija:
Norint sukurti minimalią krūvą iš nerūšiuoto masyvo, galima naudoti krūvos didinimo operaciją. Tai atliekama pradedant nuo paskutinio ne lapo mazgo ir pakartotinai atliekant burbulo mažinimo operaciją, kol visi mazgai patenkins krūvos savybę.
 „Heapify“ operacija „Min Heap“.
     „Heapify“ operacijos įgyvendinimas „Min-Heap“:    
C++ #include  #include  using namespace std; void minHeapify(vector &arr, int i, int n) { int mažiausias = i;  int l = 2*i + 1;  int r = 2*i + 2;  jei (l< n && arr[l] < arr[smallest])  smallest = l;  if (r < n && arr[r] < arr[smallest])  smallest = r;  if (smallest != i) {  swap(arr[i], arr[smallest]);  minHeapify(arr, smallest, n);  } } int main() {  vector arr = {10, 5, 15, 2, 20, 30};  cout<< 'Original array: ';  for (int i = 0; i < arr.size(); i++)  cout << arr[i] << ' ';  // Perform heapify operation on min-heap  for (int i = arr.size()/2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size());  cout<< '
Min-Heap after heapify operation: ';  for (int i = 0; i < arr.size(); i++)  cout << arr[i] << ' ';  return 0; }>
 Java // Java code of Heapify operation in Min-Heap import java.util.Arrays; import java.util.List; public class Main {  // Function to maintain the min-heap property of the heap rooted at index 'i'  public static void minHeapify(List arr, int i, int n) { // Tarkime, kad šaknis yra mažiausias elementas iš pradžių int mažiausias = i;  // Apskaičiuokite dabartinio mazgo kairiojo ir dešiniojo vaiko indeksus int l = 2 * i + 1;  int r = 2 * i + 2;  // Palyginkite kairįjį vaiką su dabartiniu mažiausiu if (l< n && arr.get(l) < arr.get(smallest))  smallest = l;  // Compare the right child with the current smallest  if (r < n && arr.get(r) < arr.get(smallest))  smallest = r;  // If the current node is not the smallest, swap it with the smallest child  if (smallest != i) {  int temp = arr.get(i);  arr.set(i, arr.get(smallest));  arr.set(smallest, temp);  // Recursively heapify the subtree rooted at the smallest child  minHeapify(arr, smallest, n);  }  }  public static void main(String[] args) {  // Create a list representing the array  List arr = Arrays.asList(10, 5, 15, 2, 20, 30);  System.out.print('Original masyvas: ');  // Išspausdinti pradinį masyvą (int i = 0; i< arr.size(); i++)  System.out.print(arr.get(i) + ' ');  // Perform heapify operation on the min-heap  // Start from the last non-leaf node and go up to the root of the tree  for (int i = arr.size() / 2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size());  System.out.print('
Min-Heap po krūvos formavimo operacijos: ');  // Spausdinti min-heap po heapify operacijos (int i = 0; i< arr.size(); i++)  System.out.print(arr.get(i) + ' ');  } }>
 Python def minHeapify(arr, i, n): smallest = i left = 2 * i + 1 right = 2 * i + 2 if left < n and arr[left] < arr[smallest]: smallest = left if right < n and arr[right] < arr[smallest]: smallest = right if smallest != i: arr[i], arr[smallest] = arr[smallest], arr[i] minHeapify(arr, smallest, n) if __name__ == '__main__': arr = [10, 5, 15, 2, 20, 30] print('Original array:', arr) # Perform heapify operation on a min-heap for i in range(len(arr) // 2 - 1, -1, -1): minHeapify(arr, i, len(arr)) print('Min-Heap after heapify operation:', arr)>
 C# using System; using System.Collections.Generic; class GFG {  // Function to perform the minHeapify operation on a min-heap.  static void MinHeapify(List arr, int i, int n) { int mažiausias = i;  int left = 2 * i + 1;  int dešinėje = 2 * i + 2;  // Palyginkite kairįjį vaiką su dabartiniu mažiausiu mazgu.  jei (kairėje< n && arr[left] < arr[smallest])  smallest = left;  // Compare the right child with the current smallest node.  if (right < n && arr[right] < arr[smallest])  smallest = right;  // If the current node is not the smallest  // swap it with the smallest child.  if (smallest != i)  {  int temp = arr[i];  arr[i] = arr[smallest];  arr[smallest] = temp;  // Recursively call minHeapify on the affected subtree.  MinHeapify(arr, smallest, n);  }  }  static void Main(string[] args)  {  List arr = naujas sąrašas { 10, 5, 15, 2, 20, 30 };  Console.Write('Original masyvas: ');  foreach (int num in arr) Console.Write(skaičius + ' ');  // Atlikite heapify operaciją min-heap.  for (int i = arr.Count / 2 - 1; i>= 0; i--) MinHeapify(arr, i, arr.Count);  Console.Write('
Min-Heap po krūvos formavimo operacijos: ');  foreach (int num in arr) Console.Write(skaičius + ' ');  } }>>Javascript= 0; i--) minHeapify(arr, i, arr.length);  // Spausdinti min-heap po heapify operacijos console.log('Min-Heap po heapify operacijos: ' + arr.join(' ')); } // Iškvieskite pagrindinę funkciją, kad pradėtumėte procesą main();>>  
  Išvestis  Min. krūvos krūvos sudėtingumas yra O(n).
 5. Paieškos operacija „Min-Heap“ duomenų struktūroje:
Norint ieškoti elemento min. krūvoje, galima atlikti tiesinę paiešką masyve, kuris reiškia krūvą. Tačiau linijinės paieškos laiko sudėtingumas yra O (n), o tai nėra efektyvu. Todėl paieška nėra dažniausiai naudojama operacija mažoje krūvoje.
 Pateikiame kodo pavyzdį, rodantį, kaip ieškoti elemento mažoje krūvoje naudojant    std::rasti()    :
C++ #include  using namespace std; int main() {  priority_queue , didesnis > min_heap;  // pavyzdys max heap min_heap.push(10);  min_heap.push(9);  min_heap.push(8);  min_heap.push(6);  min_heap.push(4);  int element = 6; // elementas ieškoti bool rastas = false;  // Nukopijuokite min krūvą į laikiną eilę ir ieškokite // elemento std::priority_queue , didesnis > temp = min_krūva;  while (!temp.empty()) { if (temp.top() == elementas) { rasta = tiesa;  pertrauka;  } temp.pop();  } if (rasta) { std::cout<< 'Element found in the min heap.'  << std::endl;  }  else {  std::cout << 'Element not found in the min heap.'  << std::endl;  }  return 0; }>
 Java import java.util.PriorityQueue; public class GFG {  public static void main(String[] args)  {  PriorityQueue min_heap = new PriorityQueue();  min_heap.add(3); // įterpti elementus į prioritetinę eilę min_heap.offer(1);  min_heap.offer(4);  min_heap.offer(1);  min_heap.offer(6);  int element = 6; // elementas, kurio reikia ieškoti loginio rasta = false;  // Nukopijuokite min krūvą į laikiną eilę ir ieškokite // elemento PriorityQueue temp = new PriorityQueue(min_heap);  while (!temp.isEmpty()) { if (temp.poll() == element) { rasta = tiesa;  pertrauka;  } } if (rasta) { System.out.println( 'Elementas rastas min. krūvoje.');  } else { System.out.println( 'Elementas nerastas min. krūvoje.');  } } }>
 Python3 import heapq min_heap = [1, 2, 3, 5, 6, 7, 8, 10] # example min heap heapq.heapify(min_heap) element = 6 # element to search for found = False # Copy the min heap to a temporary list and search for the element temp = list(min_heap) while temp: if heapq.heappop(temp) == element: found = True break if found: print('Element found in the min heap.') else: print('Element not found in the min heap.')>
 C# using System; using System.Collections.Generic; public class GFG {  public static void Main()  {  var minHeap = new PriorityQueue ();  // pavyzdys min krūva minHeap.Enqueue(4);  minHeap.Enqueue(6);  minHeap.Enqueue(8);  minHeap.Enqueue(9);  minHeap.Enqueue(10);  int element = 6; // elementas ieškoti bool rastas = false;  // Nukopijuokite min krūvą į laikiną eilę ir ieškokite // elemento var temp = new PriorityQueue (minHeap);  while (temp.Count> 0) { if (temp.Peek() == element) { rasta = tiesa;  pertrauka;  } temp.Dequeue();  } if (rasta) { Console.WriteLine( 'Elementas rastas min. krūvoje.');  } else { Console.WriteLine( 'Elementas nerastas min. krūvoje.');  } } }>
 Javascript // Example min heap let minHeap = new PriorityQueue(); minHeap.enqueue(4); minHeap.enqueue(6); minHeap.enqueue(8); minHeap.enqueue(9); minHeap.enqueue(10); let element = 6; // Element to search for let found = false; // Copy the min heap to a temporary queue and search for the element let temp = new PriorityQueue(minHeap); while (temp.size()>0) { if (temp.peek() == elementas) { rasta = tiesa;  pertrauka;  } temp.dequeue(); } if (rasta) { console.log('Elementas rastas min. krūvoje.'); } else { console.log('Elementas nerastas min. krūvoje.'); }>
   
  Išvestis  The    laiko sudėtingumas    šios programos yra    O(n log n)    , kur    n    yra elementų skaičius prioritetinėje eilėje.
 Įterpimo operacija turi laiko sudėtingumą    O(log n)    blogiausiu atveju, nes reikia prižiūrėti krūvos turtą. Paieškos operacija apima prioritetinės eilės nukopijavimą į laikinąją eilę, o tada laikiną eilę, kuri užtrunka    O(n log n)    laikas blogiausiu atveju, nes kiekvieną elementą reikia nukopijuoti ir ištraukti iš eilės, o prioritetinę eilę reikia sukurti iš naujo kiekvienai operacijai.
 The    erdvės sudėtingumas    programos dalis yra    O(n)    nes saugo    n    elementus prioritetinėje eilėje ir sukuria laikiną eilę su    n    elementai.
 Min-Heap duomenų struktūros pritaikymai:
    Krūvos rūšiavimas:    Minimali krūva naudojama kaip pagrindinis krūvos rūšiavimo algoritmo komponentas, kuris yra efektyvus rūšiavimo algoritmas, kurio laiko sudėtingumas yra O(nlogn).
    Prioritetinė eilė:    Prioritetinė eilė gali būti įdiegta naudojant minimalią krūvos duomenų struktūrą, kurioje elementas su mažiausia verte visada yra šaknyje.
    Dijkstra algoritmas:    Dijkstra algoritme mini krūva naudojama grafiko viršūnėms saugoti su minimaliu atstumu nuo pradinės viršūnės. Viršūnė su mažiausiu atstumu visada yra krūvos šaknyje.
    Huffmano kodavimas:    Naudojant Huffmano kodavimą, minimali krūva naudojama prioritetinei eilei sukurti, kad būtų sukurtas optimalus priešdėlio kodas tam tikram simbolių rinkiniui.
    Sujungti K surūšiuotus masyvus:    Atsižvelgdami į K surūšiuotus masyvus, galime efektyviai sujungti juos į vieną surūšiuotą masyvą, naudodami minimalią krūvos duomenų struktūrą.
Min-heap duomenų struktūros pranašumai:
    Veiksmingas įterpimas ir ištrynimas    : Mini krūva leidžia greitai įterpti ir ištrinti elementus, kurių laiko sudėtingumas yra O(log n), kur n yra elementų skaičius krūvoje.
    Veiksmingas minimalaus elemento gavimas:    Minimalus elementas min krūvoje visada yra krūvos šaknyje, kurią galima gauti per O(1) laiką.
    Erdvės taupymas:    Minimali krūva yra kompaktiška duomenų struktūra, kurią galima įgyvendinti naudojant masyvą arba dvejetainį medį, todėl ji efektyviai užima erdvę.
    Rūšiavimas:    Minimali krūva gali būti naudojama norint įgyvendinti efektyvų rūšiavimo algoritmą, pvz., krūvos rūšiavimą, kurio laiko sudėtingumas yra O(n log n).
    Prioritetinė eilė:    Minimali krūva gali būti naudojama prioritetinei eilei įgyvendinti, kai elementą su minimaliu prioritetu galima efektyviai nuskaityti per O(1) laiką.
    Universalumas:    „Min heap“ turi keletą kompiuterių mokslo programų, įskaitant grafikų algoritmus, duomenų glaudinimą ir duomenų bazių sistemas.
Apskritai min krūva yra naudinga ir universali duomenų struktūra, kuri siūlo efektyvias operacijas, erdvės efektyvumą ir turi keletą programų kompiuterių moksle.
	Min. krūva	Max Heap
1.	Min-Heap raktas, esantis šakniniame mazge, turi būti mažesnis arba lygus tarp visų antrinių raktų.	„Max-Heap“ šakniniame mazge esantis raktas turi būti didesnis arba lygus tarp visų antrinių raktų.
2.	Min-Heap minimalus pagrindinis elementas yra šaknyje.	Max-Heap didžiausias pagrindinis elementas yra šaknyje.
3.	Min-Heap naudoja didėjantį prioritetą.	Max-Heap naudoja mažėjantį prioritetą.
4.	Konstruojant „Min-Heap“ pirmenybė teikiama mažiausiam elementui. java sujungimo eilutės	„Max-Heap“ konstrukcijoje pirmenybė teikiama didžiausiam elementui.
5.	Min-Heap mažiausias elementas yra pirmasis, kuris iškeliamas iš krūvos.	Max-Heap didžiausias elementas yra pirmasis, kuris ištraukiamas iš krūvos.