Tradicinių dvejetainių paieškos medžių apribojimai gali būti varginantys. Susipažinkite su B-Tree – daugiafunkcine duomenų struktūra, kuri gali lengvai apdoroti didžiulius duomenų kiekius. Kai reikia saugoti ir ieškoti didelių duomenų kiekių, tradiciniai dvejetainiai paieškos medžiai gali tapti nepraktiški dėl prasto našumo ir didelio atminties naudojimo. B-medžiai, taip pat žinomi kaip B-medis arba subalansuotas medis, yra savaiminio balansavimo medžio tipas, kuris buvo specialiai sukurtas šiems apribojimams įveikti.
Skirtingai nuo tradicinių dvejetainių paieškos medžių, B-Trees pasižymi dideliu skaičiumi raktų, kuriuos jie gali saugoti viename mazge, todėl jie taip pat žinomi kaip dideli raktų medžiai. Kiekviename B medžio mazge gali būti keli raktai, o tai leidžia medžiui turėti didesnį šakojimosi koeficientą, taigi ir mažesnį aukštį. Dėl tokio nedidelio aukščio disko įvesties/išvesties reikia mažiau, todėl paieškos ir įterpimo operacijos yra greitesnės. „B-Trees“ ypač tinka saugojimo sistemoms, turinčioms lėtą, didelių duomenų prieigą, pvz., standžiuosius diskus, „flash“ atmintį ir CD-ROM.
B-Trees palaiko pusiausvyrą, užtikrindama, kad kiekvienas mazgas turėtų minimalų raktų skaičių, todėl medis visada yra subalansuotas. Šis balansas garantuoja, kad operacijų, tokių kaip įterpimas, trynimas ir paieška, sudėtingumas visada yra O(log n), neatsižvelgiant į pradinę medžio formą.
B-medžio laiko sudėtingumas:
| ponas Nr. | Algoritmas | Laiko sudėtingumas |
|---|---|---|
| 1. | Paieška | O(log n) |
| 2. | Įdėti | O(log n) |
| 3. | Ištrinti | O(log n) |
Pastaba: n yra bendras elementų skaičius B medyje
mvc java
B-Tree savybės:
- Visi lapai yra tame pačiame lygyje.
- B medis apibrėžiamas terminu minimalus laipsnis ' t ‘. vertė ' t “ priklauso nuo disko bloko dydžio.
- Kiekviename mazge, išskyrus šaknį, turi būti bent t-1 raktai. Šaknyje gali būti mažiausiai 1 Raktas.
- Visuose mazguose (įskaitant šaknį) gali būti daugiausia ( 2*t – 1 ) raktai.
- Mazgo vaikų skaičius lygus jame esančių raktų skaičiui plius 1 .
- Visi mazgo raktai rūšiuojami didėjančia tvarka. Vaikas tarp dviejų raktų k1 ir k2 yra visi raktai diapazone nuo k1 ir k2 .
- B-Tree auga ir traukiasi nuo šaknų, o tai skiriasi nuo dvejetainės paieškos medžio. Dvejetainiai paieškos medžiai auga žemyn ir taip pat traukiasi žemyn.
- Kaip ir kiti subalansuoti dvejetainiai paieškos medžiai, paieškos, įterpimo ir ištrynimo laikas yra O(log n).
- Mazgas įterpiamas į B medį tik lapo mazge.
Toliau pateikiamas 5 minimalaus užsakymo B medžio pavyzdys
Pastaba: kad praktiniuose B medžiuose minimalaus užsakymo vertė yra daug didesnė nei 5.

Aukščiau pateiktoje diagramoje matome, kad visi lapų mazgai yra tame pačiame lygyje ir visi ne lapai neturi tuščio pomedžio ir turi vienu raktus mažiau nei jų vaikų skaičius.
Įdomūs faktai apie B medžius:
- Mažiausias B medžio aukštis, kuris gali egzistuoti su n mazgų skaičiumi ir m yra didžiausias mazgo vaikų skaičius:
- Didžiausias B medžio aukštis, kuris gali egzistuoti su n mazgų skaičiumi, o t yra mažiausias vaikų skaičius, kurį gali turėti ne šakninis mazgas:
ir
Perėjimas per B medį:
Traversal taip pat panašus į Inorder traversal of Binary Tree. Pradedame nuo kairiojo vaiko, rekursyviai spausdiname kairėje esantį vaiką, tada pakartojame tą patį procesą likusiems vaikams ir raktams. Pabaigoje rekursyviai atspausdinkite dešinėje esantį vaiką.
Paieškos operacija B-Tree:
Paieška yra panaši į paiešką dvejetainiame paieškos medyje. Raktas, kurio reikia ieškoti, yra k.
- Pradėkite nuo šaknies ir rekursyviai eikite žemyn.
- Už kiekvieną aplankytą ne lapų mazgą,
- Jei mazgas turi raktą, mes tiesiog grąžiname mazgą.
- Kitu atveju mes pasikartojame iki atitinkamo mazgo antrinio (vaiko, kuris yra prieš pat pirmąjį didesnį raktą).
- Jei pasiekiame lapo mazgą ir lapo mazge nerandame k, grąžinkite NULL.
B-medžio paieška yra panaši į dvejetainio medžio paiešką. Algoritmas yra panašus ir eina su rekursija. Kiekviename lygyje paieška optimizuojama taip, tarsi rakto reikšmės nėra pirminio diapazone, tada raktas yra kitoje šakoje. Kadangi šios vertės riboja paiešką, jos taip pat žinomos kaip ribinės vertės arba atskyrimo reikšmės. Jei pasieksime lapo mazgą ir nerasime norimo rakto, jis parodys NULL.
Elemento paieškos B medyje algoritmas:
C++
struct> Node {> >int> n;> >int> key[MAX_KEYS];> >Node* child[MAX_CHILDREN];> >bool> leaf;> };> Node* BtreeSearch(Node* x,>int> k) {> >int> i = 0;> >while> (i n && k>x->key[i]) {> >i++;> >}> >if> (i n && k == x->raktas [i]) {> >return> x;> >}> >if> (x->lapas) {> >return> nullptr;> >}> >return> BtreeSearch(x->vaikas [i], k);> }> |
>
>
C
BtreeSearch(x, k)> >i = 1> > >// n[x] means number of keys in x node> >while> i ? n[x] and k ? keyi[x]> >do> i = i + 1> >if> i n[x] and k = keyi[x]> >then>return> (x, i)> >if> leaf [x]> >then>return> NIL> >else> >return> BtreeSearch(ci[x], k)> |
>
>
Java
class> Node {> >int> n;> >int>[] key =>new> int>[MAX_KEYS];> >Node[] child =>new> Node[MAX_CHILDREN];> >boolean> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i =>0>;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Python3
class> Node:> >def> __init__(>self>):> >self>.n>=> 0> >self>.key>=> [>0>]>*> MAX_KEYS> >self>.child>=> [>None>]>*> MAX_CHILDREN> >self>.leaf>=> True> def> BtreeSearch(x, k):> >i>=> 0> >while> i and k>= x.key[i]: i += 1, jei i ir k == x.key[i]: grąžinti x, jei x.lapas: grąžinti Nėra grąžinti BtreeSearch(x.child[i], k)> |
>
>
C#
class> Node {> >public> int> n;> >public> int>[] key =>new> int>[MAX_KEYS];> >public> Node[] child =>new> Node[MAX_CHILDREN];> >public> bool> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Javascript
// Define a Node class with properties n, key, child, and leaf> class Node {> >constructor() {> >this>.n = 0;> >this>.key =>new> Array(MAX_KEYS);> >this>.child =>new> Array(MAX_CHILDREN);> >this>.leaf =>false>;> >}> }> // Define a function BtreeSearch that takes in a Node object x and an integer k> function> BtreeSearch(x, k) {> >let i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Pavyzdžiai:
java pabaiga
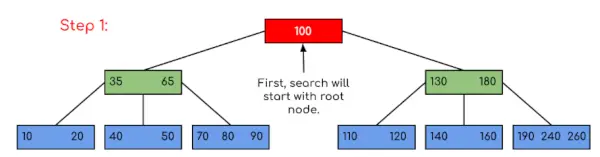
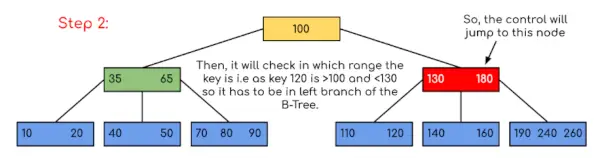
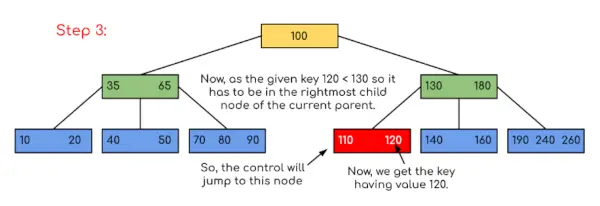
Įvestis: Ieškokite 120 nurodytame B medyje.
Sprendimas:
hadoop pamoka
Šiame pavyzdyje matome, kad mūsų paieška buvo sumažinta tiesiog apribojant tikimybę, kur gali būti raktas, kuriame yra reikšmė. Panašiai, jei pirmiau pateiktame pavyzdyje turime ieškoti 180, tada valdiklis sustos ties 2 žingsniu, nes programa nustatys, kad raktas 180 yra dabartiniame mazge. Ir panašiai, jei reikia ieškoti 90, tada kaip 90 <100, taigi jis automatiškai pereis į kairįjį pomedį, todėl valdymo srautas vyks panašiai, kaip parodyta aukščiau esančiame pavyzdyje.
Toliau pateikiamas pirmiau minėto metodo įgyvendinimas:
C++
// C++ implementation of search() and traverse() methods> #include> using> namespace> std;> // A BTree node> class> BTreeNode {> >int>* keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode** C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> public>:> >BTreeNode(>int> _t,>bool> _leaf);>// Constructor> >// A function to traverse all nodes in a subtree rooted> >// with this node> >void> traverse();> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode*> >search(>int> k);>// returns NULL if k is not present.> >// Make the BTree friend of this so that we can access> >// private members of this class in BTree functions> >friend> class> BTree;> };> // A BTree> class> BTree {> >BTreeNode* root;>// Pointer to root node> >int> t;>// Minimum degree> public>:> >// Constructor (Initializes tree as empty)> >BTree(>int> _t)> >{> >root = NULL;> >t = _t;> >}> >// function to traverse the tree> >void> traverse()> >{> >if> (root != NULL)> >root->traverse();> >}> >// function to search a key in this tree> >BTreeNode* search(>int> k)> >{> >return> (root == NULL) ? NULL : root->paieška(k);> >}> };> // Constructor for BTreeNode class> BTreeNode::BTreeNode(>int> _t,>bool> _leaf)> {> >// Copy the given minimum degree and leaf property> >t = _t;> >leaf = _leaf;> >// Allocate memory for maximum number of possible keys> >// and child pointers> >keys =>new> int>[2 * t - 1];> >C =>new> BTreeNode*[2 * t];> >// Initialize the number of keys as 0> >n = 0;> }> // Function to traverse all nodes in a subtree rooted with> // this node> void> BTreeNode::traverse()> {> >// There are n keys and n+1 children, traverse through n> >// keys and first n children> >int> i;> >for> (i = 0; i // If this is not leaf, then before printing key[i], // traverse the subtree rooted with child C[i]. if (leaf == false) C[i]->traverse(); cout<< ' ' << keys[i]; } // Print the subtree rooted with last child if (leaf == false) C[i]->traverse(); } // Funkcija ieškoti rakto k submedyje su šiuo mazgu BTreeNode* BTreeNode::search(int k) { // Rasti pirmąjį raktą, didesnį arba lygų k int i = 0; while (i klavišai[i]) i++; // Jei rastas raktas lygus k, grąžinkite šį mazgą if (keys[i] == k) grąžina šį; // Jei raktas čia nerastas ir tai yra lapo mazgas if (leaf == true) return NULL; // Eiti į atitinkamą antrinį return C[i]->search(k); }> |
>
>
Java
// Java program to illustrate the sum of two numbers> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >System.out.println();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >boolean> >leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>boolean> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[>2> * t ->1>];> >this>.C =>new> BTreeNode[>2> * t];> >this>.n =>0>;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i =>0>;> >for> (i =>0>; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >System.out.print(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i =>0>;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> |
>
>
Python3
# Create a node> class> BTreeNode:> >def> __init__(>self>, leaf>=>False>):> >self>.leaf>=> leaf> >self>.keys>=> []> >self>.child>=> []> # Tree> class> BTree:> >def> __init__(>self>, t):> >self>.root>=> BTreeNode(>True>)> >self>.t>=> t> ># Insert node> >def> insert(>self>, k):> >root>=> self>.root> >if> len>(root.keys)>=>=> (>2> *> self>.t)>-> 1>:> >temp>=> BTreeNode()> >self>.root>=> temp> >temp.child.insert(>0>, root)> >self>.split_child(temp,>0>)> >self>.insert_non_full(temp, k)> >else>:> >self>.insert_non_full(root, k)> ># Insert nonfull> >def> insert_non_full(>self>, x, k):> >i>=> len>(x.keys)>-> 1> >if> x.leaf:> >x.keys.append((>None>,>None>))> >while> i>>> and> k[>0>] 0]: x.keys[i + 1] = x.keys[i] i -= 1 x.keys[i + 1] = k else: while i>= 0 ir k[0] 0]: i -= 1 i += 1, jei len(x.vaikas[i].raktai) == (2 * self.t) - 1: self.split_child(x, i) if k[0]> x.keys[i][0]: i += 1 self.insert_non_full(x.child[i], k) # Padalykite antrinį def split_child(self, x, i): t = self. .t y = x.vaikas[i] z = BTreeNode(y.leaf) x.child.insert(i + 1, z) x.keys.insert(i, y.keys[t - 1]) z.keys = y.keys[t: (2 * t) - 1] y.keys = y.keys[0: t - 1], jei ne y.leaf: z.child = y.child[t: 2 * t] y. vaikas = y.child[0: t - 1] # Spausdinti medį def print_tree(self, x, l=0): print('Level ', l, ' ', len(x.keys), end=':') for i in x.keys: print(i, end=' ') print() l += 1 if len(x.child)> 0: for i in x.child: self.print_tree(i, l) # Paieškos raktas medyje def search_key(self, k, x=None): jei x nėra Nėra: i = 0, o i |
>
>
C#
// C# program to illustrate the sum of two numbers> using> System;> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >Console.WriteLine();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>bool> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[2 * t - 1];> >this>.C =>new> BTreeNode[2 * t];> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i = 0;> >for> (i = 0; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >Console.Write(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >public> BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i = 0;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by Rajput-Ji> |
>
>
Javascript
// Javascript program to illustrate the sum of two numbers> // A BTree> class Btree> {> >// Constructor (Initializes tree as empty)> >constructor(t)> >{> >this>.root =>null>;> >this>.t = t;> >}> > >// function to traverse the tree> >traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >document.write(>' '>);> >}> > >// function to search a key in this tree> >search(k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> > }> // A BTree node> class BTreeNode> {> >// Constructor> >constructor(t,leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> Array(2 * t - 1);> >this>.C =>new> Array(2 * t);> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted with this node> >traverse()> >{> >// There are n keys and n+1 children, traverse through n keys> >// and first n children> >let i = 0;> >for> (i = 0; i <>this>.n; i++) {> > >// If this is not leaf, then before printing key[i],> >// traverse the subtree rooted with child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >document.write(keys[i] +>' '>);> >}> > >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> > >// A function to search a key in the subtree rooted with this node.> >search(k)>// returns NULL if k is not present.> >{> > >// Find the first key greater than or equal to k> >let i = 0;> >while> (i keys[i])> >i++;> > >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> > >// If the key is not found here and this is a leaf node> >if> (leaf ==>true>)> >return> null>;> > >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by patel2127> |
>
>
Pastaba: Aukščiau pateiktame kode nėra tvarkyklės programos. Visą programą aprašysime kitame mūsų įraše B-medžio įterpimas .
Yra dvi sutartys, skirtos apibrėžti B medį, viena – apibrėžti minimaliu laipsniu, antra – apibrėžti tvarka. Mes laikėmės minimalaus laipsnio konvencijos ir to laikysimės būsimuose „B-Tree“ įrašuose. Aukščiau pateiktoje programoje naudojami kintamųjų pavadinimai taip pat išlieka tokie patys
kaip atidaryti failą su java
B-trees pritaikymas:
- Jis naudojamas didelėse duomenų bazėse norint pasiekti duomenis, saugomus diske
- Duomenų paieška duomenų rinkinyje gali būti atlikta per daug trumpesnį laiką naudojant B-Tree
- Naudojant indeksavimo funkciją, galima pasiekti kelių lygių indeksavimą.
- Dauguma serverių taip pat naudoja B-medžio metodą.
- B-medžiai naudojami CAD sistemose geometriniams duomenims tvarkyti ir ieškoti.
- B-medžiai taip pat naudojami kitose srityse, tokiose kaip natūralios kalbos apdorojimas, kompiuterių tinklai ir kriptografija.
B-medžių pranašumai:
- „B-Trees“ turi garantuotą O(log n) laiko sudėtingumą pagrindinėms operacijoms, tokioms kaip įterpimas, trynimas ir paieška, todėl jie tinka dideliems duomenų rinkiniams ir realaus laiko programoms.
- B-medžiai yra savaime išsibalansuojantys.
- Didelis lygiagretumas ir didelis našumas.
- Efektyvus saugyklos naudojimas.
B formos medžių trūkumai:
- B-medžiai yra pagrįsti disko duomenų struktūromis ir gali naudoti daug disko.
- Ne visais atvejais geriausias.
- Lėtas, palyginti su kitomis duomenų struktūromis.
Įterpimas ir ištrynimas:
B-medžio įterpimas
B-medžio ištrynimas