Dvejetainio medžio aukštis arba gylis gali būti apibrėžtas kaip maksimalus arba didžiausias kraštų skaičius nuo lapo mazgo iki šaknies mazgo arba šaknies mazgo iki lapo mazgo. Šakninis mazgas bus nuliniame lygyje, o tai reiškia, kad jei šakninis mazgas neturi su juo susietų antrinių mazgų, konkretaus dvejetainio medžio aukštis arba gylis laikomas nuliu.
Paimkime pavyzdį, kad geriau suprastume dvejetainio medžio aukštį.
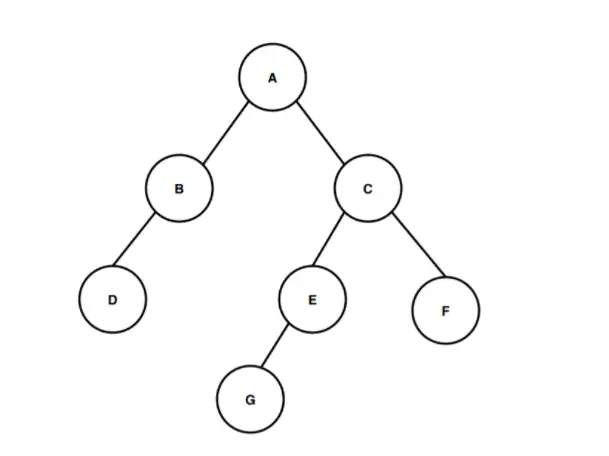
Aukščiau esančiame paveikslėlyje turime dvejetainį medį, prasidedantį nuo šakninio mazgo, pavadinto A. Šakninis mazgas A turi du antrinius mazgus B ir C, kaip atitinkamai kairįjį ir dešinįjį. Panašiai kairiajame antriniame mazge B yra tik vienas kairysis antrinis mazgas, pavadintas D, o dešinysis antrinis mazgas C turi du antrinius mazgus E ir F, iš kurių mazgas E turi mazgą G kaip vienintelį kairįjį.
j e s t
Dabar apskaičiuokime šio dvejetainio medžio aukštį. Apskaičiuojant dvejetainio medžio aukštį, suskaičiuokite kraštų skaičių nuo šaknies mazgo iki giliausio lapo mazgo. Giliausias mazgas, esantis šiame dvejetainiame medyje, yra mazgas G. Taigi, norėdami apskaičiuoti šio dvejetainio medžio aukštį arba gylį, turime apskaičiuoti kraštų skaičių tarp šaknies mazgo ir giliausio mazgo G. Pirmasis kraštas yra nuo mazgo A iki mazgo C, antrasis kraštas yra nuo mazgo C iki mazgo E, o trečiasis kraštas yra nuo mazgo E iki mazgo G. Taigi, norint pereiti nuo šakninio mazgo A iki giliausio mazgo G, yra trys briaunos , taigi dvejetainio medžio aukštis arba gylis yra 3. Kelias, kuriuo ėjome pereidami nuo šaknies iki giliausio lapo mazgo, yra A > C > E > G ir šis kelias perėjimo metu apima tris kraštus, todėl pagal pagal dvejetainio medžio aukščio apibrėžimą šio dvejetainio medžio aukštis yra 3.
Būdai rasti dvejetainio medžio aukštį
Dabar parašykime kodą, kad surastume dvejetainio medžio aukštį. Yra du būdai, kaip rasti dvejetainio medžio aukštį. Vienas yra rekursinis metodas o kitas yra nerekursyvus metodas kuri naudos eilės duomenų struktūrą dvejetainio medžio aukščiui apskaičiuoti.
Rekursyvus būdas
Pirmiausia pažiūrėkime, kaip rekursyvus rasti dvejetainio medžio aukštį.
Kodas:
// Java program to create and to find the height of a binary tree by recursive way // util package is imported to use classes like Queue and LinkedList import java.util.*; // A class named Node is created representing a single node of a binary tree class Node{ // The class Node has three class variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree Node left, right; // a parameterized constructor is created to create and add data to the node at the same time. public Node(int item) { key = item; left = right = null; } } // end of node class definition // A public class named BinaryTree is created having two constructors and methods to print the binary tree level-wise. class BinaryTree{ // A static variable named root_node is created that will represent the node of the binary tree static Node root_node; // A parametrized constructor of the BinaryTree class is written having the key as a parameter BinaryTree(int key) { // here we are constructing a new node and assigning it to the root node root_node = new Node(key); } BinaryTree() { root_node = null; } // a public static function named print tree is created to print all the nodes in the tree level-wise starting from the root node public static void printTree() { int h = height(root_node); int i; for (i=1; i<=h; i++){ printcurrentlevel(root_node, i); system.out.println(); } a public static function named height is created to fund the of binary tree starting from root node deepest leaf that present in passed as parameter called recursively until returned null find int height(node root){ then will be zero if (root="=" null) return 0; else { * compute each subtree lheight="height(root.left);" rheight="height(root.right);" use larger one both sub trees calcualted and which higher used. (lheight> rheight) return(lheight+1); else return(rheight+1); } } // a Public static function named printCurrentLevel is created to print al the nodes that are present in that level // this function is called repeatedly for each level of the binary tree to print all the nodes in that particular level public static void printCurrentLevel (Node root ,int level) { if (root == null) return; if (level == 1) System.out.print(root.key + ' '); else if (level > 1) { printCurrentLevel(root.left, level-1); printCurrentLevel(root.right, level-1); } } //the main function is created to create an object of the BinaryTree class and call the printTree method to level-wise print the nodes of the binary tree and the height method to find the height of the binary tree public static void main(String[] args){ // first of all we have created an Object of the BinaryTree class that will represent the binary tree BinaryTree tree = new BinaryTree(); // now a new node with the value as 150 is added as the root node to the Binary Tree tree.root_node = new Node(150); // now a new node with the value 250 is added as a left child to the root node tree.root_node.left = new Node(250); // now a new node with the value 270 is added as a right child to the root node tree.root_node.right = new Node(270); // now a new node with the value 320 is added as a left child to the left node of the previous level node tree.root_node.left.left = new Node(320); // now a new node with the value 350 is added as a right child to the right node of the previous level node tree.root_node.left.right = new Node(350); /* 150 / 250 270 / / 320 350 null null */ System.out.println('Printing the nodes of tree level wise :'); System.out.println('Level order traversal : '); tree.printTree(); // height of the binary tree is calculated bypassing the root as parameter to the height() function. int h = tree.height(tree.root_node) System.out.println('The height of the Binary tree is : ' + h ); } } // end of the BinaryTree class </=h;> Išvestis: Aukščiau pateikto kodo išvestis yra tokia:
Printing the nodes of tree level wise: Level order traversal: (level 0) 150 (level 1) 250 270 (level 2) 320 350 The height of the Binary tree is: 2
Rekursyviniu būdu pavadinome aukštis () funkciją pakartotinai, kad surastų dvejetainio medžio aukštį. Dvejetainio medžio šakninis mazgas perduodamas kaip aukščio () funkcijos parametras. Funkcija height() apskaičiuoja abiejų šaknies mazgo pomedžių aukštį ir kuris iš abiejų aukščių yra didesnis, laikomas dvejetainio medžio aukščiu.
Nerekursyvus būdas
Dabar pažiūrėkime nerekursyvų būdą, kaip rasti dvejetainio medžio aukštį.
Kodas:
// A C++ program to create and to find the height of a binary tree by non recursive way // iostream header file is included to use the cin and cout objects of the istream and ostream classes respectively #include #include using namespace std; // A struct named Node is created representing a single node of a binary tree struct Node { // The struct Node has three variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree struct Node* left, *right; }; // A Function named newNode is created to add a new node to the binary tree, the newNode function has one parameter of integer type named key that will represent the value that particular new node will be storing Node* newNode(int key) { Node* temp = new Node; temp->key = key; temp->left = temp->right = NULL; return (temp); } // A function named height is created to find the height of the binary tree with non recursive way // The parameter to the height function is the root node of the binary tree that will be present at level zero // In the height function the nodes of the binary tree are added into the Queue data structure and the depth variable is incremented until // the NULL node is encountered while traversing the nodes of the binary tree stored in the Queue data structure. int height(struct Node* root){ //Initialising a variable to count the //height of tree int depth = 0; queueq; //Pushing first level element along with NULL q.push(root); q.push(NULL); while(!q.empty()){ Node* temp = q.front(); q.pop(); //When NULL encountered, increment the value if(temp == NULL){ depth++; } //If NULL not encountered, keep moving if(temp != NULL){ if(temp->left){ q.push(temp->left); } if(temp->right){ q.push(temp->right); } } //If queue still have elements left, //push NULL again to the queue. else if(!q.empty()){ q.push(NULL); } } return depth; } // Start of the main function int main() { // first of all we have created an Object of the struct Node that will represent the binary tree // the value of the root node is 10 Node *root = newNode(10); // now a new node with the value 20 is added as a left child to the root node root->left = newNode(20); // now a new node with the value 30 is added as a right child to the root node root->right = newNode(30); // now a new node with the value 40 is added as a left child to the left node of the previous level node root->left->left = newNode(40); // now a new node with the value 50 is added as a right child to the left node of the previous level node root->left->right = newNode(50); /* 10 / 20 30 / / 40 50 null null */ cout<<'the height(depth) of tree is: '<<height(root); cout<<endl; } end the main function < pre> <p> <strong>Output:</strong> </p> <pre> The Height(Depth) of the tree is: 2 </pre> <p>In this approach, we have used a non recursive way to find the depth of the binary tree. To find the height of the binary tree, we have written a function named height that will require a parameter of Node type (that means the root of the binary tree whose height needs to be calculated). The root of the binary tree is present at level zero, which means the height or depth of the root is zero.</p> <p>In the non recursive approach, we use the Queue Data Structure to find the depth of the binary tree. The nodes of the binary tree for which we want to find the depth are added to the Queue data structure with the help of an enqueue operation to which the node of the binary tree is passed as a parameter to this function.</p> <p>Once all the nodes are added to the queue, the nodes added in the queue are removed by calling the dequeue function that will keep on removing one element from the queue until the null node of the binary tree is encountered. Each time a node of the binary tree from the queue is removed, the depth variable representing the depth of the binary tree is incremented by one. And in the end, the value of the depth variable will represent the final depth of the binary tree.</p> <hr></'the> Taikydami šį metodą, mes naudojome nerekursyvų būdą dvejetainio medžio gyliui rasti. Norėdami rasti dvejetainio medžio aukštį, parašėme funkciją, pavadintą aukštis, kuriai reikės Mazgo tipo parametro (tai reiškia dvejetainio medžio šaknį, kurio aukštį reikia apskaičiuoti). Dvejetainio medžio šaknis yra nuliniame lygyje, o tai reiškia, kad šaknies aukštis arba gylis yra lygus nuliui.
java string charatas
Taikant nerekursyvų metodą, mes naudojame eilės duomenų struktūrą, kad surastume dvejetainio medžio gylį. Dvejetainio medžio mazgai, kurių gylį norime rasti, įtraukiami į eilės duomenų struktūrą, naudojant eilės operaciją, kuriai kaip šios funkcijos parametras perduodamas dvejetainio medžio mazgas.
Kai visi mazgai pridedami prie eilės, į eilę įtraukti mazgai pašalinami iškviečiant dequeue funkciją, kuri ir toliau pašalins vieną elementą iš eilės, kol bus aptiktas nulinis dvejetainio medžio mazgas. Kiekvieną kartą, kai iš eilės pašalinamas dvejetainio medžio mazgas, gylio kintamasis, reiškiantis dvejetainio medžio gylį, padidinamas vienu. Galų gale gylio kintamojo reikšmė parodys galutinį dvejetainio medžio gylį.
