Sudėtinės palūkanos – tai palūkanos, skaičiuojamos nuo paskolos ar indėlio sumos, už kurią skaičiuojamos palūkanos už pagrindinę sumą ir anksčiau uždirbtas palūkanas.

Bendras skirtumas tarp sudėtinių ir paprastų palūkanų yra tas, kad sudėtinės palūkanos , palūkanos skaičiuojamos už pagrindinę sumą ir už anksčiau uždirbtas palūkanas, o paprastosios palūkanos priklauso tik nuo investuotos pagrindinės sumos.

Turinys

• Kas yra sudėtinės palūkanos?
• Sudėtinių palūkanų formulė
• Kaip apskaičiuoti sudėtines palūkanas?
• Sudėtinių palūkanų formulė – išvedimas
• Pusmečio sudėtinių palūkanų formulė
• Ketvirčio sudėtinių palūkanų formulė
• Mėnesio sudėtinių palūkanų formulė
• Dienos sudėtinių palūkanų formulė
• Periodinio sujungimo normos formulė
• 72 taisyklė
• Metų iš eilės sudėtinės palūkanos
• Nuolatinio susiejimo palūkanų formulė
• Kai kurios kitos sudėtinės svarbos programos
• Skirtumas tarp sudėtinių palūkanų ir paprastų palūkanų
• Sudėtinių palūkanų pavyzdžiai
• Sudėtiniai interesai – praktiniai klausimai

Kas yra sudėtinės palūkanos?

Sudėtinės palūkanos yra palūkanos už pagrindinę sumą, taip pat palūkanos, uždirbtos už pagrindinę sumą. Žodis sudėtinės palūkanos susideda iš dviejų žodžių Junginys, sudarytas iš dviejų ar daugiau, o palūkanos reiškia pinigus, uždirbtus paskolinus sumą. Taigi sudėtinės palūkanos yra pinigai, uždirbti skolinant ir susideda iš dviejų rūšių palūkanų, kurios yra:

• Palūkanos nuo pagrindinės sumos

• Palūkanos už palūkanas, uždirbtas nuo pagrindinės sumos per laikotarpį

Sudėtinių palūkanų apibrėžimas

Sudėtinės palūkanos yra palūkanos, apskaičiuotos nuo pagrindinės sumos ir anksčiau uždirbtos palūkanos. Jis žymimas C.I. Tai labai naudinga investicijų ir paskolų grąžinimo tikslais. Jis taip pat žinomas kaip palūkanos.

kas yra regex java

Sudėtinės palūkanos yra labai naudingas bankininkystės ir finansų sektoriuose, taip pat yra naudingas kituose sektoriuose. Keletas jo naudojimo būdų:

• Šalies gyventojų skaičiaus augimas
• Investicijų vertė per tam tikrą laikotarpį.
• Norėdami rasti išpūstas išlaidas ir bet kurio gaminio nusidėvėjusią vertę.
• Bet kurios institucijos ar šalies augimo prognozavimui.

Sudėtinės palūkanos (C.I) = suma – pagrindinė suma

Sudėtinių palūkanų formulė

Sudėtinės palūkanos apskaičiuojama, apskaičiavus visą sumą per tam tikrą laikotarpį, remiantis palūkanų norma ir pradine pagrindine suma. Pradinei pagrindinei sumai P, metinei palūkanų normai r, laikotarpiui t metais, palūkanų sudėties per metus dažnumui n, CI apskaičiavimo formulė yra tokia:

CI = P(1 + r/100) ⁿ – P

Aukščiau pateikta sudėtinių palūkanų skaičiavimo formulė pridedama toliau pateiktoje vaizdo formoje:

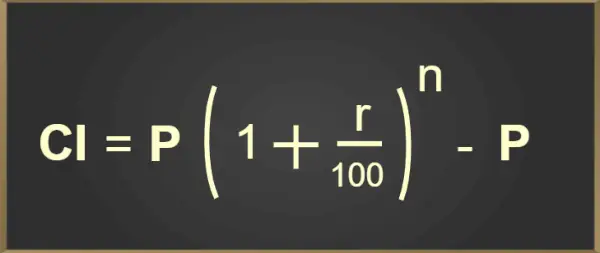
Sudėtinių palūkanų formulė

kur,

• P = pagrindinis
• r = palūkanų norma
• n = Palūkanų skaičiavimo kartų skaičius per metus
• t = laikas (metais)

Sudėtinių palūkanų formulę galime parašyti taip:

Sudėtinės palūkanos = A – P

kur,

• A = Bendra pinigų suma po sujungimo
• P = pradinė pagrindinė suma

Sudėtinės palūkanos = P(1 + r/n) ^nt -P

kur,

• P = pradinė pagrindinė suma
• r = metinė palūkanų norma
• n = Palūkanų sudėtinių kartų skaičius
• t = Metų skaičius

Sudėtinės palūkanos gali būti skaičiuojamos kasmet, kas pusę metų, kas ketvirtį, kas mėnesį, kasdien ir tt pagal reikalavimą.

Kaip apskaičiuoti sudėtines palūkanas?

Sudėtinės palūkanos yra palūkanos, mokamos tiek už pagrindinę sumą, tiek už sukauptas palūkanas. Kiekvienu intervalu uždirbtos palūkanos pridedamos prie pradinės pagrindinės sumos, todėl pagrindinė suma didėja.

Norėdami rasti sudėtines palūkanas, naudokite šiuos metodus.

1 žingsnis: Nurodyta pastaba, pagrindinė suma, norma ir laikotarpis

2 veiksmas: apskaičiuokite sumą pagal formulę A = P(1 + r/100) ⁿ

3 veiksmas: suraskite sudėtines palūkanas naudodami formulę CI = suma – pagrindinė suma

Reguliariais intervalais iki šiol sukauptos palūkanos suskaičiuojamos su esama pagrindine suma, o tada palūkanos skaičiuojamas naujam pagrindiniam mokesčiui . Nauja pagrindinė suma yra lygi Pradinės pagrindinės sumos ir iki šiol sukauptų palūkanų sumai.

Sudėtinės palūkanos = pagrindinės sumos palūkanos + pagrindinės sumos palūkanos (nuo antrųjų metų ir nuosavybėn)

Sudėtinės palūkanos skaičiuojamos reguliariais intervalais, pavyzdžiui, kasmet (kasmet), kas pusmetį, kas ketvirtį, kas mėnesį, ir tt; Panašu, kad pakartotinai investavus iš investicijos gautas palūkanų pajamas, pinigai laikui bėgant auga greičiau! Būtent tai, ką sudėtinės palūkanos daro su pinigais. Bankai ar bet kuri finansinė organizacija apskaičiuoja sumą remdamosi tik sudėtinėmis palūkanomis.

Sudėtinių palūkanų formulė – išvedimas

Sudėtinių palūkanų formulė yra galinga priemonė, naudojama finansų srityje, norint apskaičiuoti uždirbtas arba sumokėtas palūkanas nuo pradinės pagrindinės sumos, kuri apima ir pradinę pagrindinę sumą, ir per ankstesnius laikotarpius sukauptas palūkanas. Sudėtinių palūkanų formulė pateikiama taip:

kur,

• A yra būsima investicijos arba paskolos vertė, įskaitant palūkanas
• P yra pagrindinė suma (pradinė investicija arba paskolos suma)
• r yra metinė palūkanų norma (dešimtaine dalimi)
• n yra palūkanų pridėjimo kartų skaičius per metus
• t yra laikas, kuriam pinigai investuojami arba skolinami, metais

Paprasta palūkanų formulė

Paprastosios palūkanos skaičiuojamos tik nuo pagrindinės sumos. Jį galima pavaizduoti pagal formulę ,

Sudėtinių palūkanų formulė su nuolatiniu jungimu

Kai palūkanos sudedamos nepertraukiamai (be galo daug kartų per metus), sudėtinių palūkanų formulė išvesta naudojant nuolatinio sujungimo formulę:

kur,

• e yra Eulerio skaičius (apytiksliai 2,71828)
• P yra pagrindinė suma
• r yra metinė palūkanų norma
• t yra laikas metais

Bendroji sudėtinių palūkanų formulė

Norėdami gauti bendrą sudėtinių palūkanų formulę, apsvarstykite galimybę sudėti palūkanas n kartų per metus.

Jeigu P sudedama n kartų per metus taikant metinę palūkanų normą r, palūkanos r dalijamos iš n ir taikomos n kartų per metus. Taigi, po t metų formulė tampa:

kur,

• reiškia palūkanų normą per sudėtinį laikotarpį.
• nt yra bendras sudėtinių laikotarpių skaičius per t metus.

Tai formulė iliustruoja, kaip pradinė pagrindinė suma didėja laikui bėgant, kai palūkanos pridedamos reguliariais intervalais . Kai n artėja prie begalybės (t. y. nuolatinis maišymas), formulė susilieja į nepertraukiamo mišinio formulę .

Apibendrinant, sudėtinių palūkanų formulė yra nuolatinio maišymo formulės, pritaikytos atskiriems mišinio periodams per metus, rezultatas. Tai leidžia apskaičiuoti būsimą investicijos ar paskolos vertę, reguliariai įskaičiuojant sudėtines palūkanas.

Pusmečio sudėtinių palūkanų formulė

Tegul investuota pagrindinė suma yra P, o palūkanų norma yra R % per metus, kuri yra sudedama kas pusę metų „t“ metų

Kaip kas pusę metų sudėtinė suma, 6 mėnesių pabaigoje keičiama pagrindinė suma, ir iki tol uždirbtos palūkanos bus pridedamos prie pagrindinės sumos ir tada ši tampa nauja pagrindine suma. Panašiai apskaičiuojama galutinė suma.

Mes žinome,

norma = R% per metus, sudėtinis pusmetis

norma = (R/2) %

laikas yra t metų, mes žinome, kad yra t metų 2t pusę metų.

Dabar

A = P (1 + R/200) ^2t

CI = A – P

Ketvirčio sudėtinių palūkanų formulė

Tegul investuota pagrindinė suma yra P, o palūkanų norma yra R % per metus, kuri t metų sudedama kas ketvirtį.

Kaip ji sudaroma kas ketvirtį, pagrindinė suma bus pakeista 3 mėnesių pabaigoje, ir iki tol uždirbtos palūkanos bus pridedamos prie pagrindinės sumos, o tada ši tampa nauja pagrindine suma. Panašiai apskaičiuojama galutinė suma.

mes žinome,

norma = R% per metus, sudėta kas ketvirtį

norma = (R/4) %

laikas yra t metų, mes žinome, kad yra t metų 4t ketvirčiai.

Dabar

c kodo eilučių masyvas

A = P(1 + R/400) ^4t

CI = A – P

Patikrinti: Ketvirčio sudėtinių palūkanų formulė

Mėnesio sudėtinių palūkanų formulė

Jei palūkanos sudedamos kas mėnesį, sumavimo kartų skaičius bus 12, o palūkanos kiekvieną mėnesį bus 1/12 metinių sudėtinių palūkanų. Taigi mėnesinė sudėtinių palūkanų formulė pateikiama kaip

A = P[1 + (R/1200)] ^12t

CI = A – P

Patikrinti: Mėnesio sudėtinių palūkanų formulė

Dienos sudėtinių palūkanų formulė

Jei palūkanos didinamos kasdien, tada.

Nauja palūkanų norma bus R/365 %

n = 365

Taigi, dienos sudėtinių palūkanų formulė pateikiama kaip:

A = P[1 + (R/36500)] ^365t

CI = A – P

Periodinio sujungimo normos formulė

Bendra suma, įskaitant pagrindinę P sumą ir sudėtines palūkanas CI, apskaičiuojama taip:

A = P[1 + (r/n)] ^nt

kur,

• P = pagrindinis
• A = galutinė suma
• r = metinė palūkanų norma
• n = Palūkanų sudėties kartų skaičius
• t = laikas (metais)

Taigi sudėtinės palūkanos yra:

CI = A – P

72 taisyklė

72 taisyklė yra formulė, naudojama įvertinti, kiek metų mūsų pinigai padvigubėja, jei jie pridedami kasmet. Dėl pavyzdys , jei mūsų pinigai investuojami į r % kasmet, tada užtrunka 72 metus, kad mūsų pinigai padvigubėtų.

Šis skaičiavimas taip pat naudingas apskaičiuojant išpūstą mūsų pinigų vertę, y., nurodoma, per kiek metų mūsų turto vertė sumažėja perpus, jei jis kasmet nuvertėja.

72 formulės taisyklė

Ši formulė naudojama norint apskaičiuoti metų skaičių, per kurį mūsų investicijos padvigubės.

N = 72 / r

kur,

• N yra apytikslis metų skaičius, kai mūsų pinigai padvigubėja
• r yra norma, pagal kurią mūsų pinigai sudaromi kasmet

72 taisyklės pavyzdys

Tarkime, Kabiras investavo 10 00 000 rupijų į skolos fondą, kuris duoda 8% grąžą. Sužinokite, per kiek metų jos pinigai padvigubėja, jei jie pridedami kasmet.

Naudojant aukščiau pateiktą formulę: N = 72/8 = 9 metai

atsitiktinio skaičiaus c kodas

Taigi, prireikia 9 metų, kad Kabiro pinigai padvigubėtų.

Metų iš eilės sudėtinės palūkanos

Jei turime tą pačią sumą ir vienodą palūkanų normą. C.I. konkrečių metų C.I visada yra didesnis nei ankstesnių metų C.I. (3 metų PI yra didesnis nei 2 metų PI). Skirtumas tarp KI bet kuriuos dvejus metus iš eilės yra vienerių metų palūkanos už praėjusių metų C.I.

3 metų C.I – 2 metų C.I = 2 metų C.I × r × 1/100

Skirtumas tarp bet kurių dvejų iš eilės einančių metų sumų yra vienerių metų palūkanos nuo praėjusių metų sumos.

3 metų suma – 2 metų suma = 2 metų suma × r × 1/100

Pagrindiniai rezultatai

Kai turime tą pačią sumą ir tą patį kursą ,

n-tųjų metų C.I = (n – 1) metų C.I + (n – 1) metų C.I vienerių metų palūkanos

Nuolatinio susiejimo palūkanų formulė

Nepertraukiamo sujungimo formulė finansuose naudojama galutinei investicijos vertei apskaičiuoti, kuri yra nuolat derinama per skirtingą laikotarpį, o vertė pridedama per tam tikrą laiką. Nepertraukiamo mišinio formulė pateikta kaip

Galutinė vertė = dabartinė vertė × e ^rt

kur,

• r yra palūkanų norma
• t laikas

Sužinokite daugiau, Nepertraukiamo mišinio formulė

Kai kurios kitos sudėtinės svarbos programos

Augimas: Tai daugiausia naudojama augimui, jei pramonės šakos yra susijusios.

Gamyba po n metų = pradinė gamyba × (1 + r/100) ⁿ

Nusidėvėjimas: Kai prekės savikaina kasmet nuvertėja r%, tai po n metų jos vertė yra

Dabartinė vertė × (1 + r/100) ⁿ

Gyventojų problemos: kai mieste, mieste ar kaime gyventojų skaičius per metus didėja tam tikru tempu.

Gyventojų skaičius po n metų = dabartinė populiacija × (1 + r/100) ⁿ

Skirtumas tarp sudėtinių palūkanų ir paprastų palūkanų

Apie skirtumą tarp sudėtinių palūkanų ir paprastų palūkanų galite sužinoti toliau šiame straipsnyje

Sudėtinių palūkanų pavyzdžiai

Kai kurie sudėtinių palūkanų formulių pavyzdžiai:

1 pavyzdys: Raskite sudėtines palūkanas, kai pagrindinė suma = 6000 Rs, norma = 10% per metus ir laikas = 2 metai.

Sprendimas:

Palūkanos už pirmuosius metus = (6 000 × 10 × 1) / 100 = 600

Suma pirmųjų metų pabaigoje = 6000 + 600 = 6600

Palūkanos už antrus metus = (6600 × 10 × 1) / 100 = 660

Suma antrųjų metų pabaigoje = 6600 + 660 = 7260

Sudėtinės palūkanos = 7260–6000 = 1260

2 pavyzdys: kokios bus sudėtinės 8000 rupijų palūkanos per dvejus metus, kai palūkanų norma yra 2% per metus?

Sprendimas:

Atsižvelgiant į

• Pagrindinis P = 8000
• Norma r = 2 %
• Laikas = 2 metai

pagal formulę

A = P (1 + R/100) ⁿ

A = 8000 (1 + 2/100)²= 8000 (102/100)²

A = 8323

Sudėtinės palūkanos = A – P = 8323 – 8000 = 323 Rs

3 pavyzdys: Hari įnešė Rs. 4000 su finansų įmone 2 metams su 5% metinėmis palūkanomis. Kokios yra sudėtinės palūkanos, kurias Rohitas gauna po 2 metų?

Sprendimas:

Atsižvelgiant į

• Pagrindinis P = 4000
• Norma r = 5 %
• Laikas = 2 metai

Pagal formulę,

A = P (1 + R/100)ⁿ

A = 4000 (1 + 5/100)²

A = 4000 (105/100)²

A = 4410

Sudėtinės palūkanos = A – P = 4410 – 4000 = 410

4 pavyzdys: Raskite Rs sudėtines palūkanas. 2000 m., taikant 4 % metinį tarifą 1,5 metų. Kai palūkanos skaičiuojamos kas pusę metų?

Sprendimas:

Atsižvelgiant į

javafx pamoka

• Pagrindinis p = 2000
• Norma r = 4 %
• Laikas = 1,5 (t. y. 3 pusmetis)

pagal formulę,

A = P (1 + R/200) ²ⁿ

A = 2000 (1 + 4/200) ³

A = 2000 (204/200) ³

A = 2122

Sudėtinės palūkanos = A – P = 2122 – 2000 = 122

5 pavyzdys: Kokios yra 10 000 vienerių metų sudėtinės palūkanos, kurių norma yra 20 % per metus, jei palūkanos sudedamos kas ketvirtį?

Sprendimas:

Atsižvelgiant į

• Pagrindinė P = 10 000 Rs
• Norma R = 12 % (12/4 = 3 % per ketvirčio metus)
• Laikas = 1 metai (1 × 4 = 4 ketvirčiai)

Pagal formulę,

A = P (1 + R/100) ⁿ

A = 10 000 (1 + 3/100) ⁴

A = 10 000 (103/100) ⁴

A = 11255

Sudėtinės palūkanos = A – P = 11255 – 10000 = 1255

6 pavyzdys: Raskite 5% per metus sudėtines palūkanas už 2 metus nuo pagrindinės sumos, kuri per 2 metus yra 5% per metus, atsižvelgiant į Rs. 400 kaip paprastos palūkanos.

Sprendimas:

Atsižvelgiant į

• Paprastos palūkanos, JEI = 400
• norma R = 5 %
• Laikas T = 2 metai

Pagal formulę,

Paprastos palūkanos = (P × T × R)/100

⇒ P = (SI × 100) / T × R

P = (400 × 100) / 2 × 5 sudėtinių palūkanų norma = 5 %

P = 40 000/10 = 4 000 Rs

Laikas = 2 metai

Pagal formulę,

A = P (1 + R/100)

A = 4000 (1 + 5/100)

A = 4410

Sudėtinės palūkanos = A – P = 4410 – 4000 = 410

7 pavyzdys: Raskite 30 000 rupijų sudėtines palūkanas, kai 7% palūkanos sudaromos kasmet dvejus metus.

Sprendimas:

bool į eilutę java

• Pagrindinė P = 30 000 Rs
• norma R = 7 %
• Laikas = 2 metai

Pagal formulę,

A = P (1 + R/100) ⁿ

A = 30 000 (1 + 7/100) ²

A = 30 000 (107/100) ²

A = 34347

Sudėtinės palūkanos = A – P = 34347 – 30000 = 4347

Susiję skaitymai:

• Dienos sudėtinės palūkanos
• Mėnesinės sudėtinės palūkanos
• 8 klasės sudėtinių palūkanų sprendimas
• Sudėtiniai interesai – tinkamumo klausimai ir atsakymai
• Paprastas palūkanas

Sudėtiniai interesai – praktiniai klausimai

Įvairūs praktiniai klausimai dėl sudėtinių palūkanų yra:

Q1. Raskite sumą, kurią reikia sumokėti po 3 metų, jei paskolinama 10 000 suma 4% kasmet.

Q2. Raskite palūkanas, kurias reikia mokėti po 1,5 metų, jei paskolinama 2500 suma su 6% tarifu, pridedama kas pusę metų.

Q3. Apskaičiuokite sudėtines palūkanas už 9000 paskolintų 5% palūkanų normą kas ketvirtį 15 mėnesių.

4 klausimas. Apskaičiuokite sudėtines palūkanas už 20 000 paskolintų 12% palūkanų normą 3 mėnesiams, sudėtines kas mėnesį

Išvada dėl sudėtinių palūkanų

Sudėtinės palūkanos yra a galinga finansinė koncepcija, leidžianti investicijoms ar paskoloms laikui bėgant augti arba kaupti. Skirtingai nei paprastosios palūkanos, kurios skaičiuoja tik palūkanas nuo pradinės pagrindinės sumos, sudėtinės palūkanos atsižvelgiama į palūkanas, uždirbtas tiek nuo pradinės pagrindinės sumos, tiek už visas sukauptas palūkanas iš ankstesnių laikotarpių.

Sudėtinės palūkanos – DUK

Kokia sudėtinių palūkanų reikšmė?

Sudėtinės palūkanos yra palūkanos, skaičiuojamos už pagrindinę sumą, taip pat ankstesnės palūkanos, uždirbtos per fiksuotą laikotarpį

Kaip apskaičiuoti sudėtines palūkanas?

Norint apskaičiuoti sudėtines palūkanas, pirmiausia apskaičiuojama galutinė suma, tada ji atimama iš pagrindinės sumos, kad gautų galutinę sudėtines palūkanas. Suma apskaičiuojama pagal formulę,

A = P(1 + R/100) ^t

CI = A – P

Ar investuotojams sudėtinės palūkanos yra geresnės nei paprastosios palūkanos?

Taip, sudėtinės palūkanos investuotojams yra daug geresnės nei paprastosios palūkanos.

Kas yra sudėtinių palūkanų formulė, jei ji sudedama kasdien?

Tarkime, kad nurodyta pagrindinė suma yra P, norma yra R, o laiko intervalas yra T metai, tada sudėtinių palūkanų formulė, kai ji sudedama kasdien, yra:

A = P(1 + R/365) ^{{365 × T}}

Kuo skiriasi CI ir SI?

Pagrindinis skirtumas tarp CI ir SI yra SI yra palūkanos, skaičiuojamos už pagrindinę sumą, o CI yra palūkanos, skaičiuojamos už pagrindinę sumą, taip pat nuo sukauptų palūkanų už pagrindinę sumą