Rūšiuoti kibirą yra rūšiavimo technika, apimanti elementų padalijimą į įvairias grupes arba kibirus. Šie kaušeliai suformuojami tolygiai paskirstant elementus. Kai elementai yra suskirstyti į segmentus, juos galima rūšiuoti naudojant bet kurį kitą rūšiavimo algoritmą. Galiausiai surūšiuoti elementai surenkami pagal užsakymą.
Kaušelio rūšiavimo algoritmas:
Sukurti n tuščius segmentus (arba sąrašus) ir atlikite šiuos veiksmus kiekvienam masyvo elementui arr[i].
- Įterpti arr[i] į kibirą[n*masyvas[i]]
- Rūšiuokite atskirus segmentus naudodami įterpimo rūšiavimą.
- Sujunkite visus surūšiuotus kibirus.
Kaip veikia kibirų rūšiavimas?
Norėdami įvesties masyve pritaikyti rūšiavimą pagal segmentą [0,78, 0,17, 0,39, 0,26, 0,72, 0,94, 0,21, 0,12, 0,23, 0,68] , atliekame šiuos veiksmus:
1 žingsnis: Sukurkite 10 dydžio masyvą, kur kiekvienas lizdas reiškia kibirą.

Rūšiavimo kibirų kūrimas
2 žingsnis: Įdėkite elementus į segmentus iš įvesties masyvo, atsižvelgdami į jų diapazoną.
Elementų įdėjimas į kibirus:
- Paimkite kiekvieną elementą iš įvesties masyvo.
- Padauginkite elementą iš kibiro masyvo dydžio (šiuo atveju 10). Pavyzdžiui, elementui 0,23 gauname 0,23 * 10 = 2,3.
- Konvertuokite rezultatą į sveikąjį skaičių, kuris suteikia mums segmento indeksą. Šiuo atveju 2.3 paverčiamas sveikuoju skaičiumi 2.
- Įdėkite elementą į kibirą, atitinkantį apskaičiuotą indeksą.
- Pakartokite šiuos veiksmus su visais įvesties masyvo elementais.
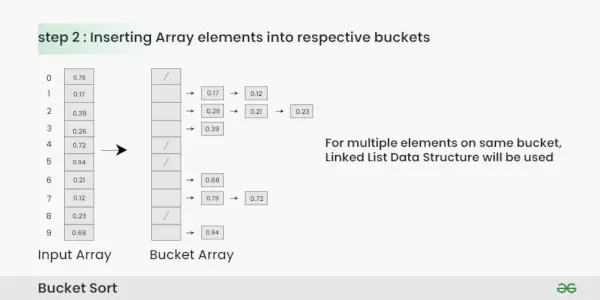
Masyvo elementų įterpimas į atitinkamus kibirus
3 veiksmas: Rūšiuokite elementus kiekviename segmente. Šiame pavyzdyje mes naudojame greitąjį rūšiavimą (arba bet kokį stabilų rūšiavimo algoritmą), kad surūšiuotume kiekvieno segmento elementus.
Elementų rūšiavimas kiekviename segmente:
- Taikykite stabilų rūšiavimo algoritmą (pvz., burbulų rūšiavimą, sujungimo rūšiavimą), kad rūšiuotumėte elementus kiekviename segmente.
- Dabar kiekvieno segmento elementai yra surūšiuoti.
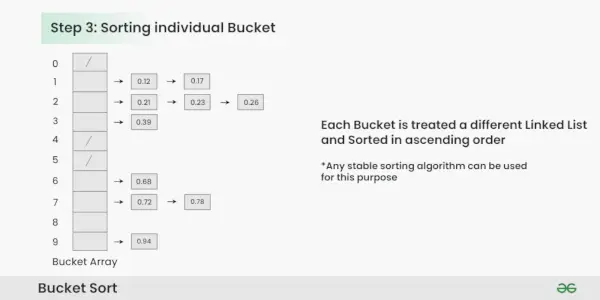
Rūšiuoti individualų kibirą
4 veiksmas: Surinkite elementus iš kiekvieno kibiro ir grąžinkite juos į pradinį masyvą.
Elementų rinkimas iš kiekvieno kibiro:
- Pakartokite kiekvieną kibirą eilės tvarka.
- Įdėkite kiekvieną atskirą elementą iš kibiro į pradinį masyvą.
- Kai elementas nukopijuotas, jis pašalinamas iš kibiro.
- Kartokite šį procesą visiems kibirams, kol bus surinkti visi elementai.
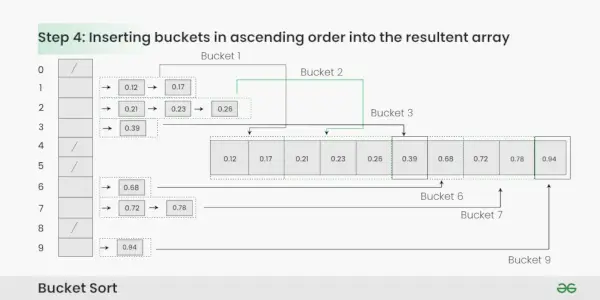
Į gautą masyvą įterpiami segmentai didėjančia tvarka
5 veiksmas: Pradiniame masyve dabar yra surūšiuoti elementai.
Galutinis surūšiuotas masyvas, naudojant segmentų rūšiavimą, yra [0,12, 0,17, 0,21, 0,23, 0,26, 0,39, 0,68, 0,72, 0,78, 0,94].

Grąžinkite surūšiuotą masyvą
Kaušelio rūšiavimo algoritmo įgyvendinimas:
Toliau pateikiamas „Bucket Sort“ diegimas:
C++ #include #include using namespace std; // Insertion sort function to sort individual buckets void insertionSort(vector& kibiras) { for (int i = 1; i< bucket.size(); ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && bucket[j]> klavišas) { bucket[j + 1] = kibiras[j]; j--; } kibiras[j + 1] = raktas; } } // Funkcija rūšiuoti n dydžio arr[] naudojant bucket sort void bucketSort(float arr[], int n) { // 1) Sukurti n tuščių segmentų vektoriųb[n]; // 2) Įdėkite masyvo elementus į skirtingus segmentus, kai (int i = 0; i< n; i++) { int bi = n * arr[i]; b[bi].push_back(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(b[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < b[i].size(); j++) { arr[index++] = b[i][j]; } } } // Driver program to test above function int main() { float arr[] = {0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434}; int n = sizeof(arr) / sizeof(arr[0]); bucketSort(arr, n); cout << 'Sorted array is
'; for (int i = 0; i < n; i++) { cout << arr[i] << ' '; } return 0; }>
Java import java.util.ArrayList; import java.util.List; public class Main { // Insertion sort function to sort individual buckets public static void insertionSort(Listkibiras) { for (int i = 1; i< bucket.size(); ++i) { float key = bucket.get(i); int j = i - 1; while (j>= 0 && bucket.get(j)> raktas) { bucket.set(j + 1, bucket.get(j)); j--; } bucket.set(j + 1, raktas); } } // Funkcija rūšiuoti n dydžio arr[] naudojant bucket sort public static void bucket(float[] arr) { int n = arr.length; // 1) Sukurkite n tuščių segmentų sąrašą[] buckets = naujas ArrayList[n]; už (int i = 0; i< n; i++) { buckets[i] = new ArrayList(); } // 2) Put array elements in different buckets for (int i = 0; i < n; i++) { int bi = (int) (n * arr[i]); buckets[bi].add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].size(); j++) { arr[index++] = buckets[i].get(j); } } } // Driver program to test above function public static void main(String[] args) { float[] arr = {0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f}; bucketSort(arr); System.out.println('Sorted array is:'); for (float num : arr) { System.out.print(num + ' '); } } }> Python def insertion_sort(bucket): for i in range(1, len(bucket)): key = bucket[i] j = i - 1 while j>= 0 ir bucket[j]> klavišas: bucket[j + 1] = bucket[j] j -= 1 bucket[j + 1] = key def bucket_sort(arr): n = len(arr) buckets = [[] for _ in range(n)] # Sudėkite masyvo elementus į skirtingus segmentus pagal skaičių in arr: bi = int(n * num) buckets[bi].append(num) # Rūšiuokite atskirus segmentus naudodami įterpimo rūšiavimo segmentą segmentuose: insertion_sort (sąrašas) # Sujungti visus segmentus į arr[] indeksas = 0 segmentui segmentuose: skaičiui segmentuose: arr[indeksas] = indekso skaičius += 1 arr = [0,897, 0,565, 0,656, 0,1234, 0,665, 0,656, 0,1234, 0,665, ]0. (arr) print('Rūšiuotas masyvas yra:') print(' '.join(map(str, arr)))> C# using System; using System.Collections.Generic; class Program { // Insertion sort function to sort individual buckets static void InsertionSort(Listkibiras) { for (int i = 1; i< bucket.Count; ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && bucket[j]> klavišas) { bucket[j + 1] = kibiras[j]; j--; } kibiras[j + 1] = raktas; } } // Funkcija rūšiuoti n dydžio arr[] naudojant bucket sort static void BucketSort(float[] arr) { int n = arr.Length; // 1) Sukurkite n tuščių segmentų sąrašą[] kibirai = naujas sąrašas[n]; už (int i = 0; i< n; i++) { buckets[i] = new List(); } // 2) Įdėkite masyvo elementus į skirtingus segmentus, skirtus (int i = 0; i< n; i++) { int bi = (int)(n * arr[i]); buckets[bi].Add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { InsertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].Count; j++) { arr[index++] = buckets[i][j]; } } } // Driver program to test above function static void Main(string[] args) { float[] arr = { 0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f }; BucketSort(arr); Console.WriteLine('Sorted array is:'); foreach (float num in arr) { Console.Write(num + ' '); } } }> JavaScript function insertionSort(bucket) { for (let i = 1; i < bucket.length; ++i) { let key = bucket[i]; let j = i - 1; while (j>= 0 && bucket[j]> klavišas) { bucket[j + 1] = kibiras[j]; j--; } kibiras[j + 1] = raktas; } } function bucketSort(arr) { tegul n = arr.length; let buckets = Array.from({ilgis: n}, () => []); // Įdėkite masyvo elementus į skirtingus segmentus (tegul i = 0; i< n; i++) { let bi = Math.floor(n * arr[i]); buckets[bi].push(arr[i]); } // Sort individual buckets using insertion sort for (let i = 0; i < n; i++) { insertionSort(buckets[i]); } // Concatenate all buckets into arr[] let index = 0; for (let i = 0; i < n; i++) { for (let j = 0; j < buckets[i].length; j++) { arr[index++] = buckets[i][j]; } } } let arr = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434]; bucketSort(arr); console.log('Sorted array is:'); console.log(arr.join(' '));> Išvestis
Sorted array is 0.1234 0.3434 0.565 0.656 0.665 0.897>
Kategorijos rūšiavimo algoritmo sudėtingumo analizė:
Laiko sudėtingumas: O (n2),
- Jei darysime prielaidą, kad įterpimas į kibirą užtrunka O (1) laiko, tada pirmiau pateikto algoritmo 1 ir 2 žingsniams aiškiai reikia O (n) laiko.
- O (1) yra lengvai įmanomas, jei mes naudojame susietą sąrašą, kad pavaizduotume segmentą.
- 4 veiksmas taip pat užtrunka O (n) laiko, nes visuose kibiruose bus n prekių.
- Pagrindinis analizės veiksmas yra 3 veiksmas. Šis veiksmas taip pat vidutiniškai trunka O(n) laiko, jei visi skaičiai yra tolygiai paskirstyti.
Pagalbinė erdvė: O(n+k)
