Dvejetainė skaičių sistema yra skaičių sistema, kuri naudojama įvairiems skaičiams pavaizduoti naudojant tik du simbolius 0 ir 1. Žodis dvejetainis yra kilęs iš žodžio bi, kuris reiškia du. Todėl ši skaičių sistema vadinama dvejetaine skaičių sistema. Taigi dvejetainė skaičių sistema yra sistema, turinti tik du simbolius.
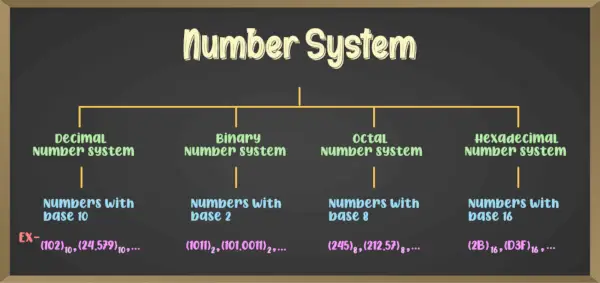
Paprastai yra įvairių tipų skaičių sistemų, tarp kurių yra keturios pagrindinės:
- Dvejetainių skaičių sistema (skaičių sistema su 2 baze)
- Aštuontainių skaičių sistema (skaičių sistema su 8 baze)
- Dešimtainė skaičių sistema (skaičių sistema su 10 baze)
- Šešioliktainė skaičių sistema (skaičių sistema su 16 baze)
Čia mes tik sužinosime apie dvejetainę skaičių sistemą. Ši skaičių sistema labai naudinga paaiškinant kompiuteriui užduotis. Dvejetainėje skaičių sistemoje turime dvi būsenas 0 ir 1 ir šias dvi būsenas vaizduoja dvi tranzistoriaus būsenos. Jei srovė teka per tranzistorių, tada kompiuteris skaito 1, o jei tranzistoriaus nėra, tada jis skaito 0. Taigi, kintamos srovės srove kompiuteris nuskaito dvejetainę skaičių sistemą. Kiekvienas skaitmuo dvejetainėje skaičių sistemoje vadinamas bitu.
Šiame straipsnyje mes išsamiai sužinosime apie dvejetainių skaičių sistemą, dvejetainių skaičių sistemos konvertavimą, dvejetainę lentelę, dvejetainių skaičių veikimą, pavyzdžius ir kt.
Turinys
- Dvejetainė skaičių sistema
- Dvejetainių skaičių lentelė
- Dvejetainis konvertavimas į dešimtainį
- Dešimtainė konvertavimas į dvejetainį
- Aritmetinės operacijos su dvejetainiais skaičiais
- Dvejetainio skaičiaus papildymas 1 ir 2
- Dvejetainių skaičių sistemos naudojimas
- Dvejetainių skaičių sistemos pavyzdys
Dvejetainė skaičių sistema
Dvejetainė skaičių sistema yra skaičių sistema, kurioje mes naudojame du skaitmenis 0 ir 1, kad atliktume visas būtinas operacijas. Dvejetainėje skaičių sistemoje turime 2 bazę. Dvejetainės skaičių sistemos bazė taip pat vadinama skaičių sistema .
Dvejetainėje skaičių sistemoje skaičių pavaizduojame kaip
- (11001)2
Aukščiau pateiktame pavyzdyje pateiktas dvejetainis skaičius, kurio bazė yra 2. Dvejetainėje skaičių sistemoje kiekvienas skaitmuo vadinamas bitu. Aukščiau pateiktame pavyzdyje yra 5 skaitmenys.
Dvejetainių skaičių lentelė
| Dešimtainis skaičius | Dvejetainis skaičius | Dešimtainis skaičius | Dvejetainis skaičius |
|---|---|---|---|
| 1 | 001 | vienuolika | 1011 m |
| 2 | 010 | 12 abstraktūs metodai | 1100 |
| 3 | 011 | 13 | 1101 |
| 4 | 100 | 14 | 1110 |
| 5 | 101 | penkiolika | 1111 |
| 6 | 110 | 16 | 10 000 |
| 7 | 111 | 17 | 10001 |
| 8 | 1000 | 18 | 10010 |
| 9 | 1001 | 19 | 10011 |
| 10 | 1010 m | dvidešimt | 10100 |
Dvejetainis konvertavimas į dešimtainį
Dvejetainis skaičius paverčiamas dešimtainiu skaičiumi, kiekvieną dvejetainio skaičiaus skaitmenį padauginus iš 1 arba 0 laipsnio iki atitinkamos laipsnio 2. Laikykime, kad dvejetainis skaičius turi n skaitmenų, B = an-1…a3a2a1a0. Dabar atitinkamas dešimtainis skaičius pateikiamas kaip
D = (a n-1 ×2 n-1 ) +…+(a 3 ×2 3 ) + (a 2 ×2 2 ) + (a 1 ×2 1 ) + (a 0 ×2 0 )
Peržiūrėkime pavyzdį, kad geriau suprastume sąvoką.
Pavyzdys: konvertuoti (10011) 2 iki dešimtainio skaičiaus.
Sprendimas:
Duotas dvejetainis skaičius yra (10011)2.
(10011)2= (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (1 × 20)
= 16 + 0 + 0 + 2 + 1 = (19)10
Taigi dvejetainis skaičius (10011)2išreiškiamas kaip (19)10.
Dešimtainė konvertavimas į dvejetainį
Dešimtainis skaičius paverčiamas dvejetainiu skaičiumi, duotą dešimtainį skaičių nuolat dalijant iš 2, kol gauname koeficientą 1, o skaičius rašome iš apačios į viršų.
Peržiūrėkime pavyzdį, kad geriau suprastume sąvoką.
Pavyzdys: konvertuoti (28) 10 į dvejetainį skaičių.
Sprendimas:
kaip skaityti csv failą java
Taigi, (28)10išreiškiamas kaip (11100)2.
Aritmetinės operacijos su dvejetainiais skaičiais
Su dvejetainiais skaičiais galime lengvai atlikti įvairias operacijas. Įvairios aritmetinės operacijos su dvejetainiu skaičiumi apima:
- Dvejetainis papildymas
- Dvejetainė atimtis
- Dvejetainis daugyba
- Dvejetainis skyrius
Dabar sužinokime apie tą patį išsamiai.
Dvejetainis papildymas
Dviejų dvejetainių skaičių sudėjimo rezultatas taip pat yra dvejetainis skaičius. Norėdami gauti dviejų dvejetainių skaičių sudėjimo rezultatą, turime pridėti dvejetainių skaičių skaitmenį po skaitmens. Toliau pateiktoje lentelėje parodyta dvejetainio sudėjimo taisyklė.
| Dvejetainis skaičius (1) | Dvejetainis skaičius (2) | Papildymas | Nešioti |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Dvejetainė atimtis
Dviejų dvejetainių skaičių atėmimo rezultatas taip pat yra dvejetainis skaičius. Norėdami gauti dviejų dvejetainių skaičių atėmimo rezultatą, dvejetainių skaičių skaitmenį turime atimti iš skaitmens. Toliau pateiktoje lentelėje parodyta dvejetainio atimties taisyklė.
| Dvejetainis skaičius (1) | Dvejetainis skaičius (2) | Atimtis | Pasiskolinti java maišant į int |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Dvejetainis daugyba
Dvejetainių skaičių daugybos procesas yra panašus į dešimtainių skaičių dauginimą. Bet kurių dviejų dvejetainių skaičių dauginimo taisyklės pateiktos lentelėje,
| Dvejetainis skaičius (1) | Dvejetainis skaičius (2) | Daugyba |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 java atidaryti failą | 1 |
Dvejetainis skyrius
The padalijimo metodas dvejetainiams skaičiams yra panašus į dešimtainio skaičių padalijimo metodą. Peržiūrėkime pavyzdį, kad geriau suprastume sąvoką.
Pavyzdys: padalinti (101101) 2 pateikė (110) 2
Sprendimas:
Dvejetainio skaičiaus papildymas 1 ir 2
- Dvejetainio skaičiaus 1 komplementas gaunamas apverčiant dvejetainio skaičiaus skaitmenis.
Pavyzdys: raskite (10011) 1 papildymą 2 .
Sprendimas:
Duotas dvejetainis skaičius yra (10011)2
Dabar, norėdami rasti jo 1 papildymą, turime invertuoti nurodyto skaičiaus skaitmenis.
Taigi, 1 papildinys iš (10011)2yra (01100)2
- Dvejetainio skaičiaus 2 komplementas gaunamas apverčiant dvejetainio skaičiaus skaitmenis ir pridedant 1 prie mažiausiai reikšmingo bito.
Pavyzdys: suraskite (1011) 2 papildymą 2 .
Sprendimas:
Duotas dvejetainis skaičius yra (1011)2
Norėdami rasti 2 papildinį, pirmiausia suraskite jo 1 papildinį, t. y. (0100)2
Dabar, pridėję 1 prie mažiausiai reikšmingo bito, gauname (0101)2
Taigi, 2 papildymas (1011)2yra (0101)2
Dvejetainių skaičių sistemos naudojimas
Dvejetainių skaičių sistemos naudojamos įvairiems tikslams, o svarbiausias dvejetainių skaičių sistemos panaudojimas yra:
- Dvejetainių skaičių sistema naudojama visoje skaitmeninėje elektronikoje įvairioms operacijoms atlikti.
- Programavimo kalbos naudoja dvejetainių skaičių sistemą duomenims koduoti ir dekoduoti.
- Dvejetainių skaičių sistema duomenų moksluose naudojama įvairiems tikslams ir kt.
Skaityti daugiau,
- Dvejetainė formulė
- Skirtumas tarp dešimtainių ir dvejetainių skaičių sistemų
Dvejetainių skaičių sistemos pavyzdys
1 pavyzdys: dešimtainio skaičiaus konvertavimas (98) 10 į dvejetainį.
Sprendimas:
Taigi dvejetainis skaičius (98)10yra lygus (1100010)2
2 pavyzdys: dvejetainio skaičiaus konvertavimas (1010101) 2 į dešimtainį skaičių.
Sprendimas:
Duotas dvejetainis skaičius, (1010101)2
= (1 × 20) + (0 × 21) + (1 × 22) + (0 × 23) + (1 × 24) + (0 × 25) + (1 × 26)
= 1 + 0 + 4 + 0 + 16 + 0 + 64
= (85)10
Taigi dvejetainis skaičius (1010101)2yra lygus (85)10dešimtainėje sistemoje.
3 pavyzdys: padalijimas (11110) 2 pateikė (101) 2
Sprendimas:
4 pavyzdys: pridėti (11011) 2 ir (10100) 2
Sprendimas:
Taigi (11011)2+ (10100)2= (101111)2
5 pavyzdys: atimti (11010) 2 ir (10110) 2
Sprendimas:
Taigi, (11010)2– (10110)2= (00100)2
6 pavyzdys: padauginkite (1110) 2 ir (1001) 2 .
Sprendimas:
Taigi, (1110)2× (1001)2= (1111110)2
DUK apie dvejetainių skaičių sistemą
Kas yra dvejetainė skaičių sistema?
Dvejetainė skaičių sistema yra viena iš keturių skaičių sistemų, kuri naudojama skaičiams pavaizduoti naudojant tik du skaitmenis – 0 ir 1. Dvejetainėje skaičių sistemoje skaitmenys vadinami „bitais“. Dvejetainių skaičių sistemą kompiuteriai naudoja įvairiems skaičiavimams atlikti.
Kas yra a B tai?
Bitas dvejetainėje skaičių sistemoje apibrėžiamas kaip atskiri skaitmenys, turintys reikšmę „0“ arba „1“.
Kas yra Nibble?
Keturių skaitmenų grupė vadinama Niblle.
Kas yra dvejetainė 10 vertė?
Dvejetainė 10 reikšmė yra (1010)2
kabinos algoritmas
Kokie yra skaičių sistemų tipai?
Yra įvairių tipų skaičių sistemų ir kai kurios iš jų yra
- Dvejetainė skaičių sistema
- Aštuontainių skaičių sistema
- Dešimtainė skaičių sistema
- Šešioliktainė skaičių sistema
Kaip apskaičiuoti dvejetainius skaičius?
Dvejetainiai skaičiai apskaičiuojami iš dvitaškių skaičių dešimtainį skaičių padalijus iš 2 ir užrašant likusią dalį. Tada mes sutvarkome visus likučius nuo naujausio iki seniausio, kad gautume dvejetainį skaičių.
Kaip pridėti dvejetainius skaičius?
Dvejetainiai skaičiai pridedami naudojant toliau pateiktas formules,
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0 (nešiokite 1)






